Условие задачи
а) Решите уравнение \(\displaystyle {{cos}^2 \frac{x}{2}}-{{sin}^2 \frac{x}{2}}={cos 2}x.\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\displaystyle \left[-\frac{3\pi }{2};0\right].\)
Решение
а) \(\displaystyle {{cos}^2 \frac{x}{2}}-{{sin}^2 \frac{x}{2}}={cos 2}x.\)
По формулам для косинуса двойного угла имеем
\({{cos}^2 \frac{x}{2}}-{{sin}^2 \frac{x}{2}}={cos x},\) а \({cos 2}x=2{{cos}^2 x}-1,\) и уравнение принимает вид
\({cos x}=2{{cos}^2 x}-1, \ 2{{cos}^2 x}-{cos x}-1=0.\)
Замена \({cos x}=t\) приводит к уравнению \(\displaystyle 2t^2-t-1=0, \; D=1+8=9, \; t=\frac{1\pm 3}{4}, \; \left[ \begin{array}{c}
t=1, \\
t=-\displaystyle \frac{1}{2}, \end{array}
\right. \ \left[ \begin{array}{c}
{cos x}=1, \\
{cos x}=-\displaystyle \frac{1}{2}. \end{array}
\right. \ \)
Рисуем тригонометрический круг и отмечаем точки, где \({cos x}=1\) или \(\displaystyle {cos x}=-\frac{1}{2}.\)
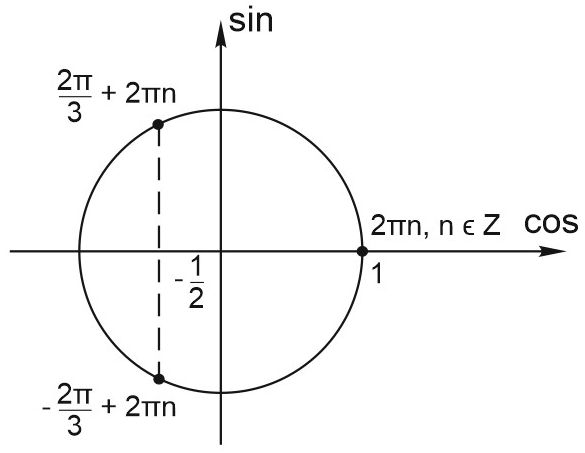
Получаем \(\displaystyle x=2\pi n, \; x=\pm \frac{2\pi }{3}+2\pi n, \; n\in Z.\)
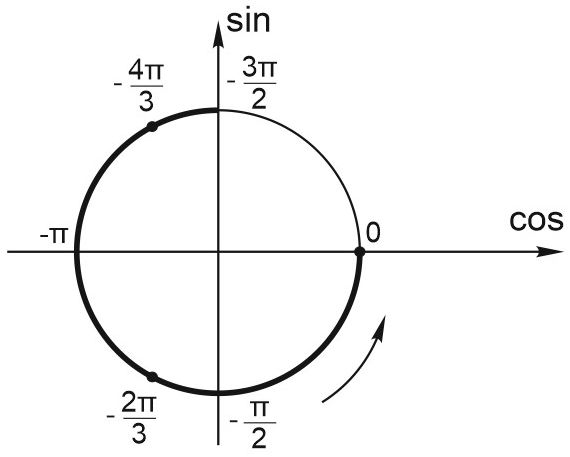
б) Отметим на тригонометрическом круге отрезок \(\displaystyle \left[-\frac{3\pi }{2};0\right]\) и найденные серии решений.
Видим, что отрезку принадлежат точки \(\displaystyle 0;\; -\frac{2\pi }{3};-\frac{2\pi }{3}-\frac{2\pi }{3}=-\frac{4\pi }{3}.\)
Ответ:
а) \(\displaystyle x=2\pi n,\; x=\pm \frac{2\pi }{3}+2\pi n,\; n\in Z.\)
б) \(\displaystyle -\frac{4\pi }{3}; -\frac{2\pi }{3}; 0.\)






























