Условие задачи
Дан прямой круговой цилиндр высотой 9 и радиусом 2. В одном из оснований проведена хорда \(AB\), равная радиусу основания, а в другом основании проведён диаметр \(CD\), перпендикулярный прямой \(AB\). Построено сечение цилиндра плоскостью \(ABNM\), перпендикулярной прямой \(CD\), причём точка \(C\) и центр основания цилиндра, содержащего отрезок \(CD\), лежат по одну сторону от плоскости сечения.
а) Докажите, что диагонали четырёхугольника \(ABNM\) равны.
б) Найдите объём пирамиды \(CABNM\).
Решение
а) Пусть \(M\) и \(N\) — проекции соответственно точек \(A\) и \(B\) на нижнее основание цилиндра, тогда \(AM\) и \(BN\) — образующие цилиндра, которые параллельны, равны и перпендикулярны плоскости основания, значит, \(AM\bot MN\). Четырёхугольник \(ABNM\), у которого противоположные стороны равны и параллельны, а соседние перпендикулярны, является прямоугольником.
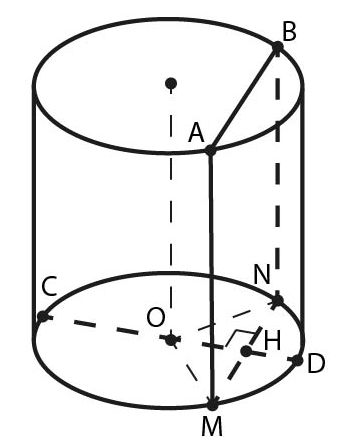
Пусть \(H\) — середина \(MN\). В равностороннем треугольнике \(MON \; OH\) — биссектриса и высота. Диаметр, проходящий через точку \(H\), и является заданным диаметром \(CD\), так как
\(\left. \begin{array}{c}
MN||AB \\
CD\bot MN \end{array}
\right\}\Rightarrow CD\bot AB\) и \(\left. \begin{array}{c}
CD\bot AB \\
CD\bot AM \end{array}
\right\}\Rightarrow CD\bot \left(ABM\right).\)
\(ABNM\) — требуемое сечение. Как показано выше, это сечение прямоугольник, а по свойству прямоугольника его диагонали \(AN\) и \(BM\) равны, что и требовалось доказать.
б) В пункте (а) доказано, что \(CD\bot \left(ABN\right), \; H=CD\cap MN,\) значит, \(CH\) — высота пирамиды. Найдём \(CH\), сделав плоский чертёж. \(CH=CO+OH,\) где \(OH\) — высота равностороннего треугольника со стороной 2, поэтому \(\displaystyle CH=2+\frac{2\sqrt{3}}{2}=2+\sqrt{3}.\)
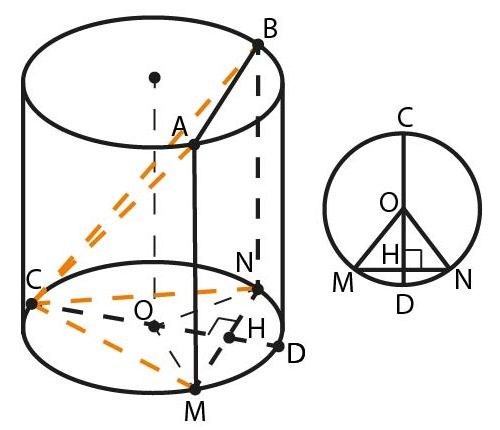
\(V_{CABNM}=\displaystyle \frac{1}{3}S_{ABNM}\cdot CH=\frac{1}{3}\cdot 9\cdot 2\left(2+\sqrt{3}\right)=6\left(2+\sqrt{3}\right). \)
Ответ:
б) \(6\left(2+\sqrt{3}\right).\)














































