Условие задачи
Решите неравенство \(\displaystyle {{{log}_2 \left(x+1\right)}}^2\cdot {{log}_{\frac{1}{3}} x^2}-4{{log}_2 \left(x+1\right)}+4{{log}_3 \left(-x\right)}+4\leq 0.\)
Решение
\(\displaystyle {{{log}_2 \left(x+1\right)}}^2\cdot {{log}_{\frac{1}{3}} x^2}-4{{log}_2 \left(x+1\right)}+4{{log}_3 \left(-x\right)}+4\leq 0.\)
Найдём ОДЗ: \(\left\{ \begin{array}{c}
x+1> 0, \\
-x>0; \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
x> -1, \\
x< 0; \end{array}
\right.\Leftrightarrow -1< x< 0.\)
Упростим \({{{log}_2 \left(x+1\right)}}^2=2{{log}_2 \left|x+1\right|}=2{{log}_2 \left(x+1\right)},\) при \(x+1>0.\)
\(\displaystyle {{log}_{\frac{1}{3}} x^2}=2{{log}_{\frac{1}{3}} \left|x\right|}=2{{log}_{\frac{1}{3}} \left(-x\right)},\) при \(-x> 0.\)
Кроме того, \(\displaystyle 2{{log}_{\frac{1}{3}} \left(-x\right)}=2\cdot \frac{{{log}_3 \left(-x\right)}}{{{log}_3 \left(\frac{1}{3}\right)}}=-2{{log}_3 \left(-x\right)}\), и переписываем неравенство
\(-2\cdot 2{{log}_2 \left(x+1\right)}\cdot {{log}_3 \left(-x\right)}-4{{log}_2 \left(x+1\right)}+4{{log}_3 \left(-x\right)}+4\leq 0.\)
Сделаем замену: \({{log}_2 \left(x+1\right)}=t, \; {{log}_3 \left(-x\right)}=z,\) тогда
\(\displaystyle -4tz-4t+4z+4\le 0\left.\right|\cdot \left(-\frac{1}{4}\right), \; tz+t-z-1\geq 0,\)
\(t\left(z+1\right)-\left(z+1\right)\geq 0, \; \left(z+1\right)\left(t-1\right)\geq 0.\)
Вернёмся к переменной \(x\).
\(\left\{ \begin{array}{c}
\left({{log}_3 \left(-x\right)}+1\right)\left({{log}_2 \left(x+1\right)}-1\right)\geq 0, \\
-1< x< 0. \end{array}
\right.\)
Записывая \(-1={{log}_3 3^{-1}}, \ {{log}_3 \left(-x\right)}+1={{log}_3 \left(-x\right)}-{{log}_3 3^{-1}}\) и, используя метод замены множителя, получаем:
\(\left\{ \begin{array}{c}
\left(-x-\displaystyle \frac{1}{3}\right)\left(x-1\right)\geq 0, \\
-1< x< 0; \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
\left(x+\displaystyle \frac{1}{3}\right)\left(x-1\right)\leq 0, \\
-1< x< 0. \end{array}
\right.\)
Отмечаем на числовой оси точки, в которых первое неравенство обращается в 0, рисуем параболу и отмечаем ОДЗ.
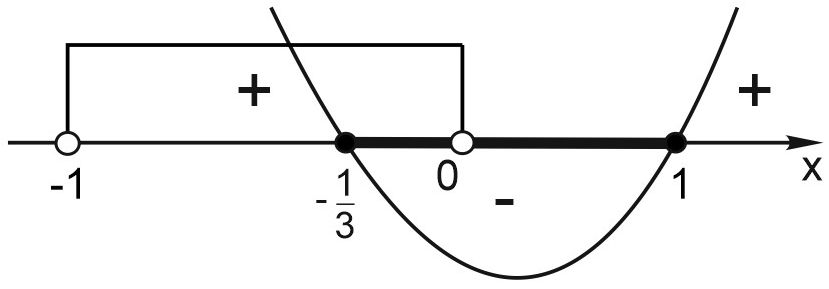
Записываем ответ: \(\displaystyle x\in \left[ -\frac{1}{3};0\right).\)
Ответ:
\(\displaystyle x\in \left [-\frac{1}{3};0\right).\)






























