Условие задачи
Прямая, проходящая через вершину \(B\) прямоугольника \(ABCD\) перпендикулярно диагонали \(AC\), пересекает сторону \(AD\) в точке \(M\), равноудалённой от вершин \(B\) и \(D\).
а) Докажите, что \(\angle ABM=30^\circ .\)
б) Найдите расстояние от центра прямоугольника до прямой \(CM\), если \(BC = 9.\)
Решение
а) \(\triangle ABH\sim \triangle ACB\) по двум углам. А так как \(\triangle ACB=\triangle DBC\) (по свойству прямоугольника), то \(\triangle ABH\sim \triangle DBC,\) поэтому \(\angle ABH=\angle DBC.\)
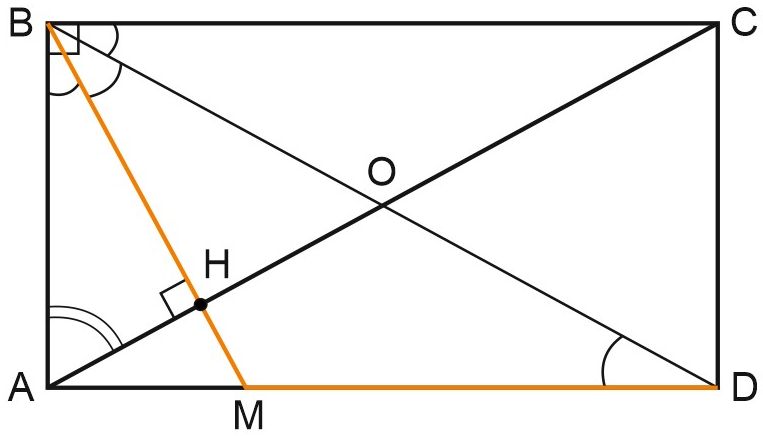
По условию \(BM=MD,\) поэтому треугольник \(BMD\) — равнобедренный, значит, \(\angle MBD=\angle MDB.\)
Кроме того, \(\angle MDB=\angle DBC,\) как внутренние накрест лежащие при параллельных сторонах прямоугольника. следовательно, \(\angle ABM=\angle ABH=\angle MBD=\angle DBC, \; 3\angle ABM=90^\circ , \; \angle ABM=30^\circ ,\) что и требовалось доказать.
б) Расстояние от точки \(O\) — центра прямоугольника до прямой \(MC\) можно найти как высоту \(h\) треугольника \(OMC\) по методу площадей.
\(\displaystyle S_{\triangle OMC}=\frac{1}{2}S_{\triangle AMC}=\frac{1}{2}\cdot \frac{1}{3}S_{\triangle ACD}=\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{3}S_{ABCD}=\frac{1}{12}S_{ABCD}=\frac{1}{12}\cdot AD\cdot AB.\)
\(AD=BC=9.\)
В прямоугольном треугольнике \(ABM\) катет \(AM\) лежит против угла в \(30^\circ \) и значит, \(BM=2AM,\) а \(BM=DM=2AM\) и \(AD=3AM=9,\) т. е. \(AM=3, \; BM=6.\)
По теореме Пифагора \(AB=\sqrt{6^2-3^2}=3\sqrt{3}, \; MC=\sqrt{6^2+{\left(3\sqrt{3}\right)}^2}=3\sqrt{7}.\)
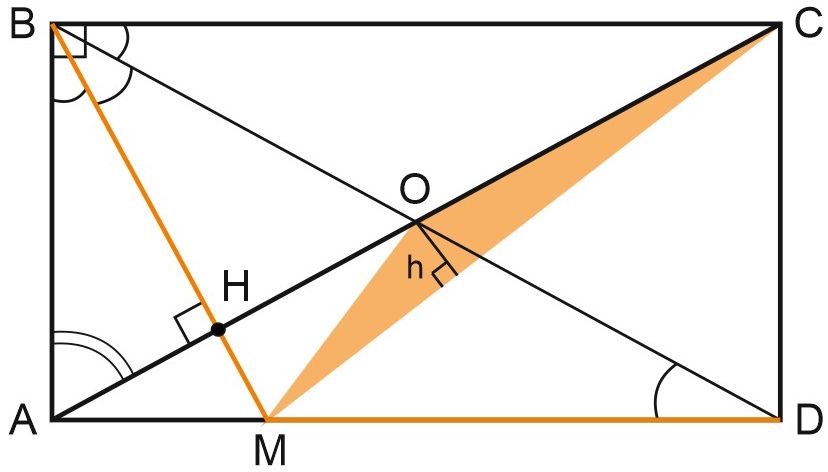
\(\displaystyle S_{\triangle OMC}=\frac{1}{12}\cdot AD\cdot AB=\frac{9\cdot 3\sqrt{3}}{12}=\frac{9\sqrt{3}}{4}, \)
\(\displaystyle S_{\triangle OMC}=\frac{1}{2}\cdot MC\cdot h=\frac{3\sqrt{7}}{2}\cdot h, \; \frac{9\sqrt{3}}{4}=\frac{3\sqrt{7}}{2}\cdot h, \; h=\frac{3\sqrt{3}}{2\sqrt{7}}.\)
Ответ:
б) \(\displaystyle \frac{70\sqrt{7}}{3}.\)






























