Условие задачи
а) Решите уравнение: \(\sqrt{3}tg\left(7\pi -2x\right)=-1.\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-2\pi ;-\displaystyle \frac{\pi }{2}\right].\)
Решение
а) \(\sqrt{3}tg\left(7\pi -2x\right)=-1.\)
Тангенс — функция с периодом \(\pi ,\) поэтому перепишем уравнение в виде \(\sqrt{3}tg\left(-2x\right)=-1,\) а с учётом нечётности преобразуем далее \(\displaystyle -\sqrt{3}tg2x=-1\Leftrightarrow \sqrt{3}tg2x=1\Leftrightarrow tg2x=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}.\)
Рисуем на тригонометрическом круге угол, соответствующий такому тангенсу, и выписываем ответ:
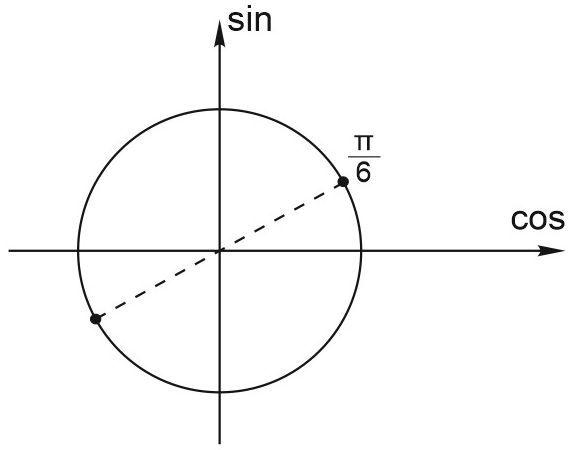
\(\displaystyle 2x=\frac{\pi }{6}+\pi n, \; n\in Z, \; x=\frac{\pi }{12}+\frac{\pi n}{2}, \; n\in Z.\)
б) Отмечаем на тригонометрическом круге отрезок \(\displaystyle \left[-2\pi ; -\frac{\pi }{2}\right]\) и найденную серию решений.
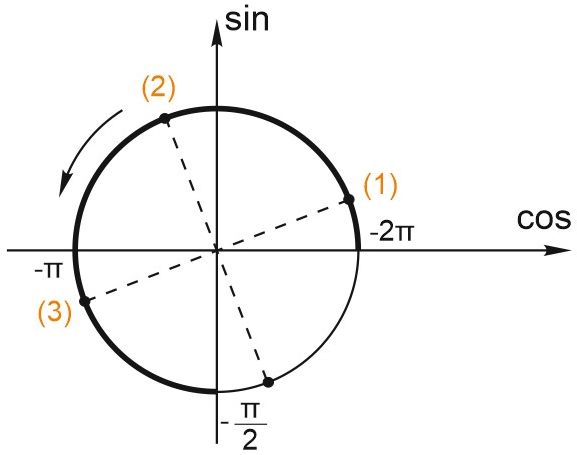
Видим, что указанному отрезку принадлежат точки
(1) \(\displaystyle -2\pi +\frac{\pi }{12}=-\frac{23\pi }{12},\) (2) \(\displaystyle -\frac{23\pi }{12}+\frac{\pi }{2}=-\frac{17\pi }{12}\) и (3) \(\displaystyle -\frac{23\pi }{12}+\pi =-\frac{11\pi }{12}.\)
Ответ:
а) \(\displaystyle \frac{\pi }{12}+\frac{\pi n}{2}, \; n\in Z;\) б) \(\displaystyle -\frac{23\pi }{12}; -\frac{17\pi }{12}; -\frac{11\pi }{12}.\)






























