Условие задачи
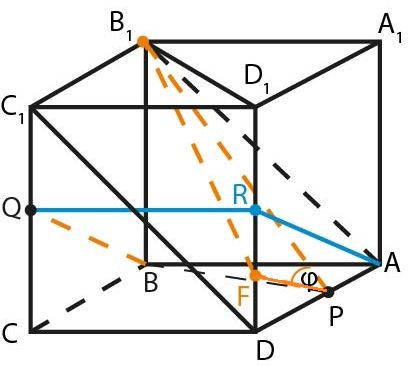
Точки \(P\) и \(Q\) — середины рёбер \(AD\) и \(CC_1\) куба \(ABCDA_1B_1C_1D_1\) соответственно.
а) Докажите, что прямая \(BQ\) перпендикулярна прямой \(B_1P.\)
б) Пусть \(H\) — проекция точки \(Q\) на прямую \(B_1P.\) Найдите \(PH\), если \(AB=12.\)
Решение
а) Проведём \(BQ\) в плоскости грани \(\left(BB_1C_1\right),\) в плоскости \(\left(B_1C_1D\right)\) проведём \(B_1P.\)
Чтобы определить угол между этими прямыми в плоскости правой грани \(\left(ADD_1\right)\) построим прямую, параллельную \(BQ\). Для этого соединим точку \(Q\) с серединой ребра \(DD_1\) точкой \(R\), получим прямую \(QR\), параллельную \(CD\).
Через параллельные прямые \(QR\) и \(AB\) проведём плоскость, которая пересечёт \(\left(ADD_1\right)\) по прямой \(AR\).
Прямые \(BQ\) и \(AR\) параллельны как линии пересечения двух параллельных плоскостей \(\left(BCC_1\right)\) и \(\left(ADD_1\right)\) третьей.
Пусть \(\displaystyle F\in DD_1, \ FD=\frac{1}{4}DD_1=\frac{1}{2}RD. \; PF\) — средняя линия \(\triangle ARD,\) поэтому \(FP||AR||QB,\) значит, угол \(\varphi \) между прямыми \(BQ\) и \(B_1P\) — это угол \(B_1PF, \; \varphi =\angle B_1PF.\)
Рассмотрим \(\triangle B_1FP\) и найдём его стороны, считая ребро куба равным \(a\).
1)\(\displaystyle FP=\sqrt{PD^2+FD^2}=\sqrt{{\left(\frac{a}{2}\right)}^2+{\left(\frac{a}{4}\right)}^2}=\frac{a\sqrt{5}}{4}.\)
2)Проведём диагональ \(B_1D_1, \; B_1D_1=a\sqrt{2}\) и из прямоугольного \(\triangle B_1D_1F\) найдём \(\displaystyle D_1F=\frac{3}{4}a, \; B_1F=\sqrt{2a^2+\frac{9}{16}a^2}=\frac{a\sqrt{41}}{4}.\)
3)\(\triangle B_1AP\) — прямоугольный, так как \(AD\bot \left(ABB_1\right),\) значит, \(AD\bot AB_1, \; B_1P\) — гипотенуза, \(\displaystyle B_1P=\sqrt{AP^2+AB^2_1}=\sqrt{\frac{a^2}{4}+2a^2}=\frac{3}{2}a.\)
Итак, \(\displaystyle FP^2=\frac{5a^2}{16}, \; B_1P^2=\frac{9a^2}{4}=\frac{36a^2}{16}, \; \)
\(B_1F^2=\displaystyle \frac{41a^2}{16}; \; B_1F^2=FP^2+B_1P^2.\)
По теореме, обратной к теореме Пифагора, получаем, что \(\triangle B_1FP\) — прямоугольный, \(\angle B_1PF=90^\circ ,\) следовательно, прямая \(BQ\) перпендикулярна прямой \(B_1P,\) что и требовалось доказать.
б) Пусть точка \(H\in B_1P\) и \(QH\bot B_1P.\)
\(\left. \begin{array}{c}
QH\bot B_1P \\
BQ\bot B_1P \end{array}
\right\}\Rightarrow B_1P\bot \left(BQH\right)\) по признаку перпендикулярности прямой и плоскости, тогда \(\left. \begin{array}{c}
B_1P\bot \left(BQH\right) \\
BH\in \left(BQH\right) \end{array}
\right\}\Rightarrow BH\bot B_1P.\) Следовательно, положение точки \(H\) можно определить из прямоугольного треугольника \(BB_1P,\) проведя в нём высоту на сторону \(B_1P.\)
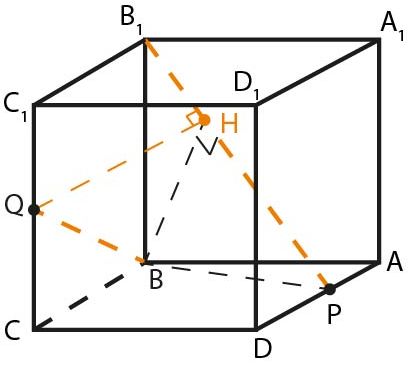
Делаем плоский чертёж.
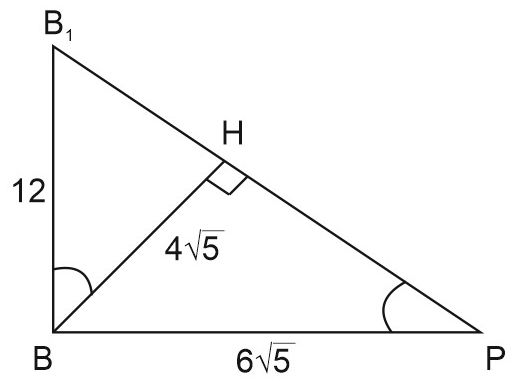
Так как ребро куба равно 12, то \(\displaystyle BB_1=12, \; B_1P=\frac{3}{2}\cdot 12=18,\) а \(BP\) находим из прямоугольного треугольника \(ABP\) по теореме Пифагора \(BP=\sqrt{AB^2+AP^2}=\sqrt{12^2+6^2}=6\sqrt{5}.\) По методу площадей для прямоугольного \(\triangle BB_1P \; B_1P\cdot BH=BB_1\cdot BP,\) откуда \(\displaystyle BH=\frac{12\cdot 6\sqrt{5}}{18}=4\sqrt{5}.\)
Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит его на два подобных треугольника \(BB_1H\) и \(PBH,\) откуда можно найти \(PH\). А можно сразу из прямоугольного треугольника \(PBH\) найти катет:
\(PH=\sqrt{PB^2-BH^2}=\sqrt{36\cdot 5-14\cdot 5}=\sqrt{20\cdot 5}=10.\)
Ответ:
б) 10.
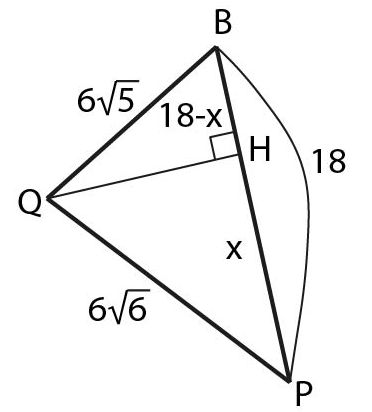
Замечание. Три точки в пространстве задают плоскость, поэтому мы можем сразу в треугольнике \(QB_1P\) найти все стороны \(\displaystyle B_1P=\frac{3}{2}\cdot 12=18,\)
\(QB_1=\sqrt{12^2+6^2}=6\sqrt{5},\)
\(QP^2=QC^2+CP^2=QC^2+CD^2+DP^2=36\cdot 6,\; QP=6\sqrt{6}.\)
Затем в треугольнике \(QB_1P\) проведём высоту \(QH,\) обозначим отрезок \(HP=x\) и, приравнивая катет \(QH\) в треугольниках \(QB_1H\) и \(QPH,\) найти \(x\).