Условие задачи
Найдите все значения \(a\), при каждом из которых множество значений функции
\(\displaystyle y=\frac{5a+150x-10ax}{100x^2+20ax+a^2+25}\) содержит отрезок \(\left[0;1\right].\)
Решение
\(\displaystyle y=\frac{5a+150x-10ax}{100x^2+20ax+a^2+25}.\)
Рассмотрим знаменатель \(100x^2+20ax+a^2+25={\left(10x+a\right)}^2+25\ge 25> 0.\)
Так как знаменатель никогда не обращается в \(0\), то функция \(y\left(x\right)\) является непрерывной на всей числовой оси. Но непрерывная функция вместе с любыми своими значениями \(A\) и \(B\) содержит и весь отрезок \(\left[A;B\right].\) Следовательно, если \(0\) и \(1\) получаются при некоторых значениях \(x\), то обязательно найдутся такие \(x\), при которых будут получаться любые значения из \(\left[0;1\right].\)
Итак, для того чтобы множество значений функции \(\displaystyle y=\frac{5a+150x-10ax}{100x^2+20ax+a^2+25}\) содержало отрезок \(\left[0;1\right],\) необходимо и достаточно, чтобы нашлись такие значения параметра \(a\), при которых одновременно будут иметь решения уравнения
\(\displaystyle \frac{5a+150x-10ax}{{\left(10x+a\right)}^2+25}=0 \; \; (1)\) и \(\displaystyle \frac{5a+150x-10ax}{{\left(10x+a\right)}^2+25}=1 \; \;(2).\)
Первое уравнение при положительном знаменателе равносильно линейному уравнению \(\left.5a+150x-10ax=0\right| :5 \Leftrightarrow \left(2a-30\right)x=a,\) которое при \(a=15\) не имеет решений, а при остальных \(a\) имеет единственный корень \(\displaystyle x=\frac{a}{2a-30}.\)
Второе уравнение при положительном знаменателе равносильно квадратному уравнению
\(100x^2+20ax+a^2+25=5a+150x-10ax\) или \(100x^2+\left(30a-150\right)x+a^2-5a+25=0\) и будет иметь решения при неотрицательном дискриминанте.
\(D={\left(30a-150\right)}^2-4\cdot \left(a^2-5a+25\right)=500\cdot \left(a^2-14a+25\right).\)
Условие \(D\ge 0\) равносильно неравенству \(a^2-14a+25\geq 0.\)
Находим корни квадратного трёхчлена:
\(\displaystyle a^2-14a+25=0, \; D=14^2-4\cdot 25=96, \; a=\frac{14\pm 4\sqrt{6}}{2}=7\pm 2\sqrt{6}\) и показываем решение.
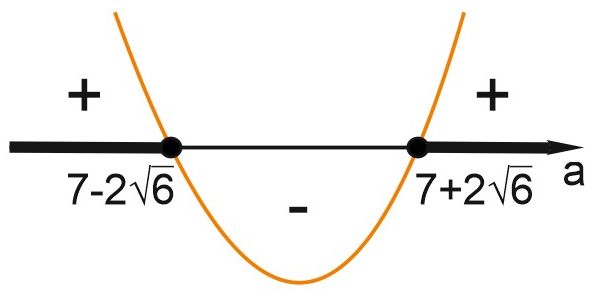
Остаётся выяснить, где на числовой оси находится число 15. Очевидно, что \(7-2\sqrt{6}< 15,\) поэтому сравним 15 со вторым корнем
\(7+2\sqrt{6}\vee 15, \; 2\sqrt{6}\vee 8, \; \sqrt{6}\vee 4, \; \sqrt{6}<4\Rightarrow 7+2\sqrt{6}< 15.\)
Уравнения (1) и (2) имеют решения при
\(a\in \left[-\infty ;7-2\sqrt{6}\right]\cup \left[7+2\sqrt{6};+\infty \right)\) и \(a\ne 15,\) и окончательно получаем
\(a\in \left(-\infty ;7-2\sqrt{6}\right]\cup \left[7+2\sqrt{6};15\right)\cup \left(15;+\infty \right).\)
Ответ:
\(a\in \left(-\infty ;7-2\sqrt{6}\right]\cup \left[7+2\sqrt{6};15\right)\cup \left(15;+\infty \right).\)




























