Условие задачи
17. Площадь параллелограмма \(ABCD\) равна 3. Точка \(H\) — середина стороны \(AD.\) Найдите площадь трапеции \(AHCB.\)
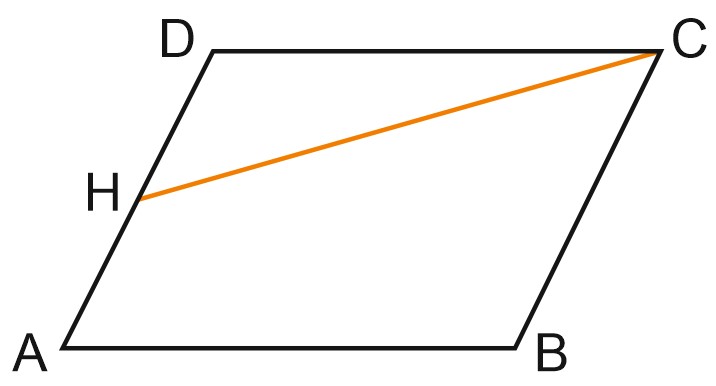
Решение
Площадь треугольника составляет четвертую часть от площади параллелограмма, тогда площадь трапеции – это \(\displaystyle \frac{3}{4}\) от площади параллелограмма.
Получим: \(S_{AHCB}=\displaystyle \frac{3}{4}\cdot 3=\frac{9}{4}=2,25.\)
Ответ:
2,25.
































