Условие задачи
19. Какие из следующих утверждений верны?
1) В треугольнике против меньшего угла лежит большая сторона.
2) Если один угол треугольника больше \(120^{\circ}\), то два других его угла меньше \(30^{\circ}.\)
3) Если все стороны треугольника меньше 1, то и все его высоты меньше 1.
4) Сумма острых углов прямоугольного треугольника не превосходит \(90^{\circ}.\)
Решение
Проверим утверждения по очереди.
1) «В треугольнике против меньшего угла лежит большая сторона» — неверно. Наоборот, в треугольнике напротив большего угла лежит большая сторона.
2) «Если один угол треугольника больше \(120^{\circ}\), то два других его угла меньше \(30^{\circ}\)» — неверно. Можно привести контрпример: треугольник с углами 120, 30 и 30 градусов.
3) «Если все стороны треугольника меньше 1, то и все его высоты меньше 1» — верно. Нарисуем произвольный треугольник \(ABC\) и проведем в нем высоту \(BH.\)
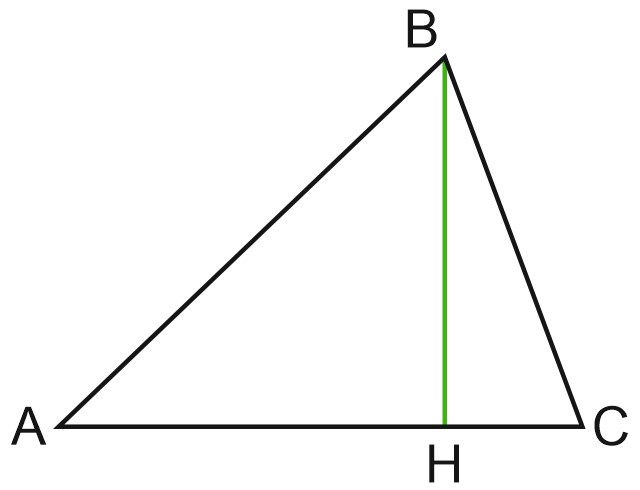
Если \(AB < 1\) и \(AC < 1\), то \(BH < 1\), так как перпендикуляр короче наклонной.
Аналогично – с двумя другими высотами треугольника.
4) «Сумма острых углов прямоугольного треугольника не превосходит \(90^{\circ}\)» — верно, сумма острых углов прямоугольного треугольника равна \(90^{\circ}.\)
Верные утверждения – это 3 и 4.
Ответ:
34.
































