Условие задачи
22. Известно, что графики функций \(y=x^2+p\) и \(y=-2x-5\) имеют ровно одну общую точку. Определите координаты этой точки. В ответе запишите координаты этой точки \(x; y.\) без пробелов.
Постройте графики заданных функций в одной системе координат.
Решение
График функции \(y=x^2+p\) – квадратичная парабола, сдвинутая на p по вертикали.
График функции \(y=-2x-5\) – прямая с угловым коэффициентом -2, проходящая через точку \((0;-5).\)
Графики этих функций имеют ровно одну общую точку, когда система уравнений
\(\left\{\begin{matrix}
y=x^2+p, \\
y=-2x-5\end{matrix}\right.\ \) имеет ровно одно решение.
Приравняем правые части этих уравнений.
\(x^2+p=-2x-5;\)
\(x^2+2x+p+5=0.\)
Это квадратное уравнение. Оно имеет ровно одно решение, если его дискриминант равен нулю.
\(D=4-4\cdot(p+5)=0;\)
\(1-p-5=0;\)
\(p=-4.\)
Если \(D=0\), то \(x=-\displaystyle \frac{2}{2}=-1.\) Тогда \(y=2-5=-3.\)
Координаты общей точки графиков: -1;-3.
Построим графики обеих функций в одной системе координат.
Подставив p в формулу первой функции, получим: \(y=x^2-4.\)
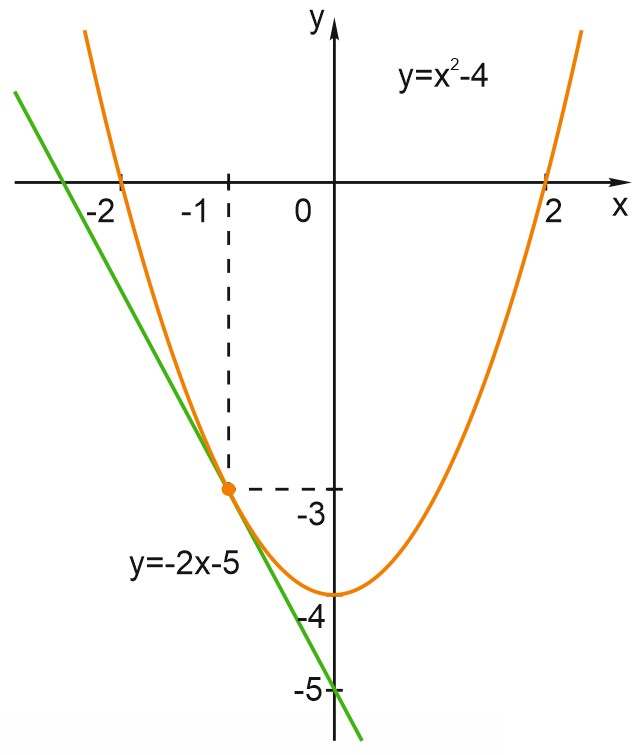
В ответе запишем без пробелов абсциссу и ординату общей точки графиков.
Обратите внимание, что здесь прямая \(y=-2x-5\) касается параболы \(y=x^2+p\). Так же, как прямая может касаться окружности.
Можно сказать, что прямая – касательная к графику функции.
Ответ:
-1;-3.
.
































