Условие задачи
23. Около окружности описана прямоугольная трапеция, периметр которой равен 32, а большая боковая сторона равна 10. Определите, на сколько одно основание трапеции больше другого.
Решение
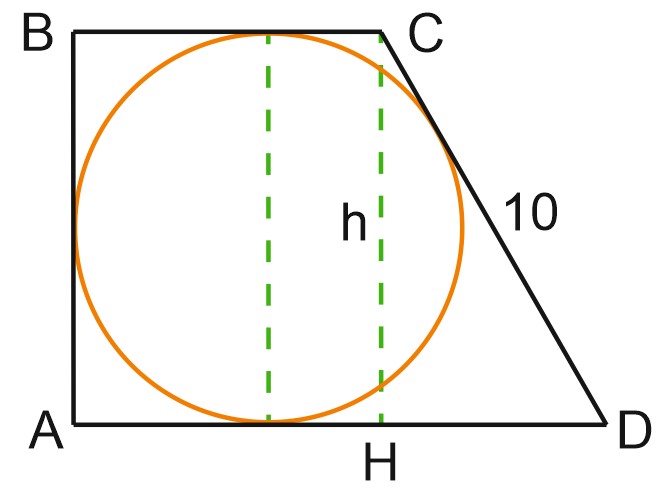
Трапеция описана вокруг окружности, значит, суммы длин ее противоположных сторон равны.
\(AB+CD=AD+BC=\displaystyle \frac{1}{2}P\), где \( P\) – периметр трапеции.
\(AB+10=32:2=16\), отсюда \(AB=6.\)
Высота \(h=AB=6\), и из прямоугольного треугольника \(CDH\) по теореме Пифагора получаем, что \(HD=8,\) откуда \(HD=AD-BC=8.\)
Ответ:
8.






























