Условие задачи
24. В остроугольном треугольнике \(ABC\) угол \(B\) равен \(60^{\circ}.\) Докажите, что точки \(A, \ C\), центр описанной окружности треугольника \(ABC\) и точка пересечения высот треугольника \(ABC\) лежат на одной окружности.
Каким из полезных фактов вы пользовались при доказательстве? Выберите правильный вариант. В ответе запишите (без точки) номер этого варианта, например: 1
1) Три высоты треугольника пересекаются в одной точке.
2) Вписанный угол равен половине центрального, опирающегося на ту же дугу.
3) Площадь треугольника равна половине произведения основания на высоту.
Решение
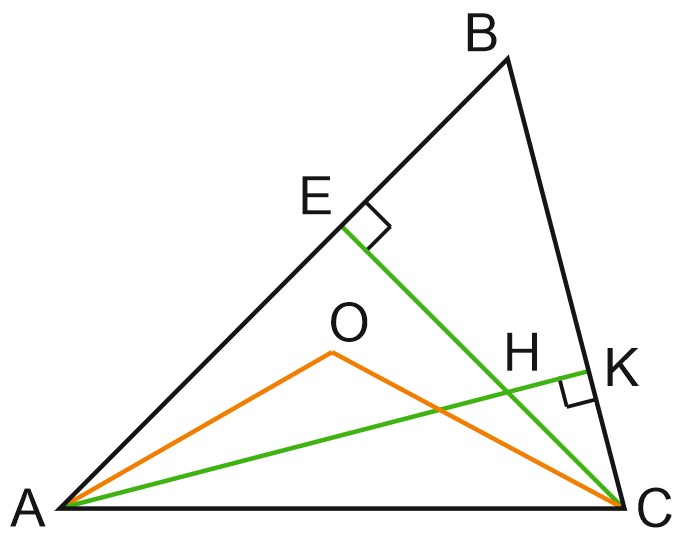
Пусть \(O\) – центр описанной окружности треугольника \(ABC, \ H\) – точка пересечения его высот.
Треугольник \(ABC\) вписан в окружность, угол \(ABC\) – вписанный, он равен половине центрального угла \(AOC\), опирающегося на ту же дугу \(AC.\)
\(\angle AOC=2\angle ABC =120^{\circ}.\)
В четырехугольнике \(BEHK\) сумма углов равна 360 градусов, углы \(E\) и \(K\) прямые, значит, сумма углов \(EHK\) и \(EBK\) равна \(180^{\circ}.\)
Углы \(AHC\) и \(EHK\) – вертикальные, они равны. Получим, что \(\angle AHC=180^{\circ}-\angle ABC=120^{\circ}.\)
Точки \(O\) и \(H\) лежат с одной стороны от отрезка \(AC\), и отрезок \(AC\) виден из этих точек под одинаковыми углами 120 градусов. Значит, точки \(A, \ O, \ H, \ C\) лежат на одной окружности.
Мы пользовались полезным фактом под номером 2.
Ответ:
2
































