Условие задачи
25. В параллелограмме \(ABCD\) проведена диагональ \(AC.\) Точка \(O\) является центром окружности, вписанной в треугольник \(ABC.\) Расстояния от точки \(O\) до точки \(A\) и прямых \(AD\) и \(AC\) соответственно равны 5, 4 и 3. Найдите площадь параллелограмма \(ABCD.\)
Решение
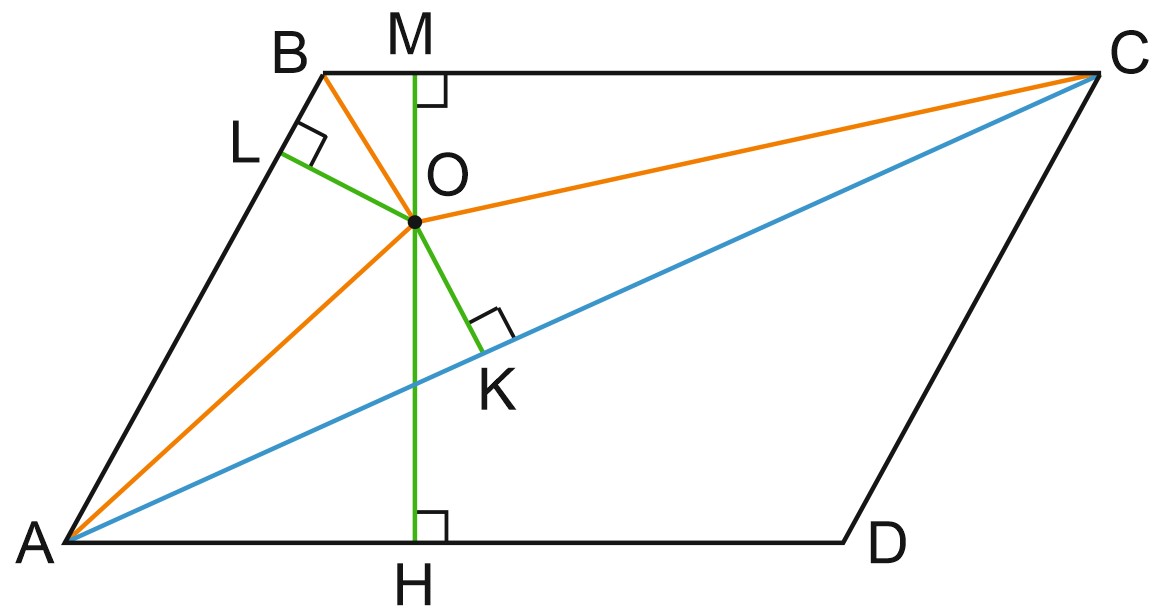
Дано: \(ABCD\) – параллелограмм, \(AC\)– диагональ.
Точка \(O\) является центром окружности, вписанной в треугольник \(ABC.\)
Пусть точки \(L, \ M\) и \(K\) - точки касания окружности со сторонами \(AB, \ BC, \ AC\) треугольника \(ABC, \ OH\) – расстояние от точки \(O\) до прямой \(AD\)
По условию, \(AO=5; OH=4; \ OK=3=OL=OM=r\) - радиус вписанной окружности.
1) Надо найти \(S_{ABCD}=a\cdot h_a.\)
По условию, \(OH⊥AD; \ OM⊥BC; \ AD∥DC.\)
Тогда \(O∈MH\), где \(MH\) – высота параллелограмма, \(MH=3+4=7.\)
2) \(\triangle AOH\) – прямоугольный. По теореме Пифагора, \(AH=3,\) т. к. \(AO=5 \) и \(OH=4.\)
3) Аналогично, \(\triangle AOK\) – прямоугольный, в нем \(AO=5; \ OK=3,\) тогда \(AK=4.\)
Значит, \(\triangle AOH=\triangle AOK\), отсюда \(\angle OAK=\angle AOH.\)
Также \(\angle OAK=\angle OAB,\) т. к. \(AO\) – биссектриса \(\angle BAC\), тогда \(\angle AOH=\angle OAB.\) Это накрест лежащие углы, поэтому \(AB∥MN.\)
Значит, \(ABCD\) – прямоугольник. \(AB=MN=7.\)
4) Найдем сторону \(BC.\)
\(O\) – центр вписанной окружности. Отрезки касательных, проведенных к окружности из одной точки, равны, поэтому
\(AK=AL=4; \ BL=BM=r=3; \ MC=CK=x.\)
Отсюда \(AB=7, \ BC=3+x, \ AC=4+x.\)
По теореме Пифагора для прямоугольного треугольника \(ABC,\)
\(AC^2=AB^2+BC^2;\)
\((4+x)^2=7^2+(3+x)^2;\)
\(16+8x+x^2=49+9+6x+x^2;\)
\(2x=42;\)
\(x=21.\)
Получили, что \(BC=3+21=24,\) тогда площадь прямоугольника:
\(S_{ABCD}=7\cdot 24=168.\)
Ответ:
168.






























