Условие задачи
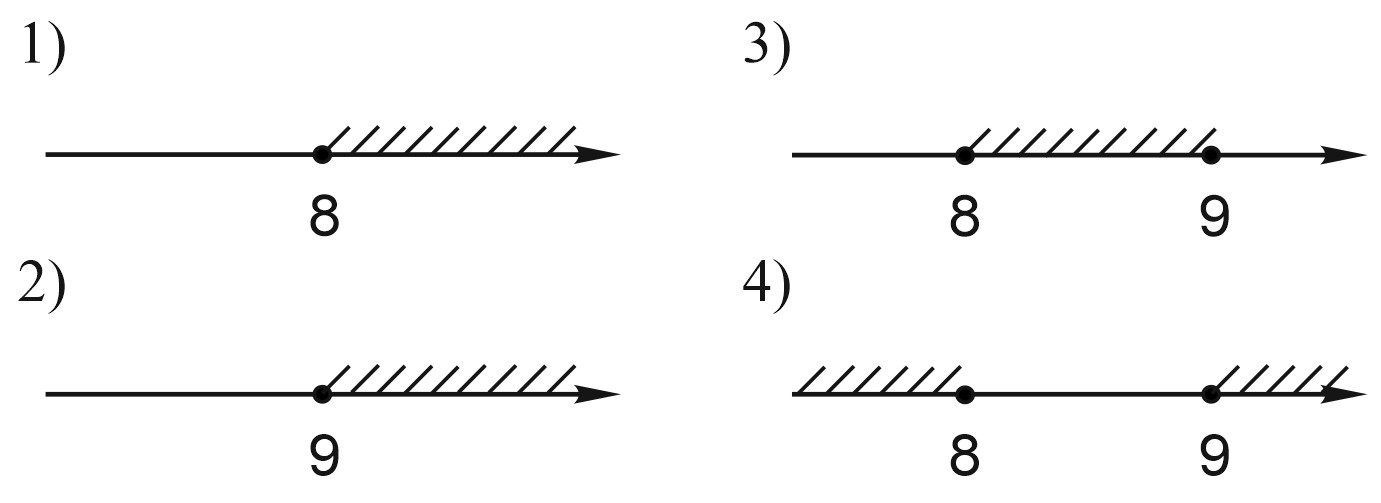
13. Решите неравенстов: \(x^2-17x+72\geq 0\). На каком из рисунков изображено множество его решений? В ответе укажите номер правильного варианта.
Решение
Применим графический метод. Найдем нули квадратичной функции
\(y=x^2-17x+72\), то есть точки пересечения параболы \(y=x^2-17x+72\) с осью \(X.\) Для этого решим уравнение \(x^2-17x+72=0.\)
По теореме Виета найдем корни: \(\left\{\begin{matrix}
x_1\cdot x_2=72, \\
x_1+x_2=17.\end{matrix}\right.\)
\(x_1=8; \ x_2=9.\)
Изобразим квадратичную параболу, ветви которой направлены вверх, пересекающую ось \(X\) в точках 8 и 9.
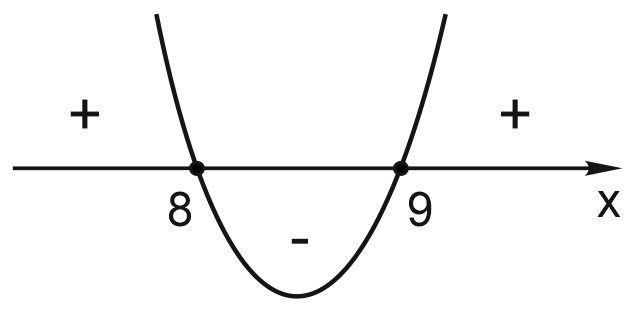
Значения этой квадратичной функции неотрицательны, если \(x\leq8\) или \(x\geq9\). Это решения нашего неравенства.
Правильный рисунок: 4.
Ответ:
4.
































