Условие задачи
17. Основания трапеции равны 6 и 10, одна из боковых сторон равна \(3\sqrt2\), а угол между ней и одним из оснований равен \(135^{\circ}\). Найдите площадь трапеции.
Решение
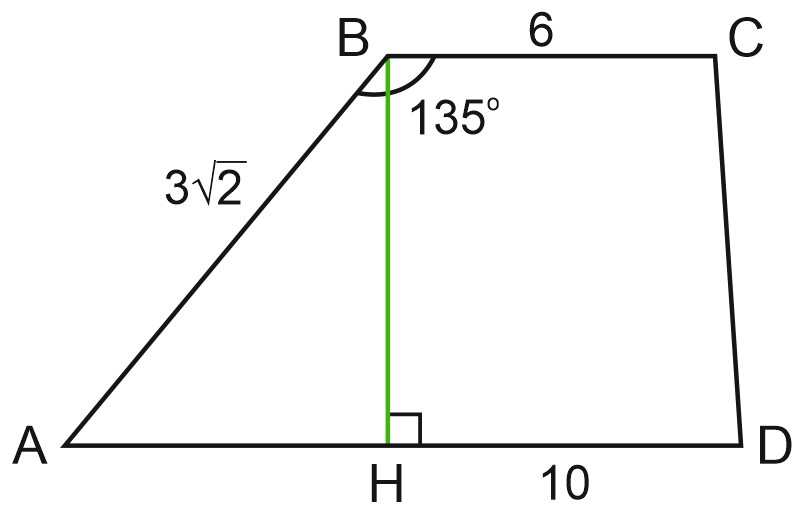
Найдем высоту трапеции \(BH\). Углы \(BAH\) и \(ABC\) – односторонние при параллельных прямых и секущей \(AB\), их сумма равна \(180\) градусов. Значит, угол \(BAH\) равен 45 градусов.
Тогда треугольник \(ABH\) – прямоугольный равнобедренный. В таком треугольнике гипотенуза в \(\sqrt2\) раз больше катета. Отсюда \(BH=AH=3.\)
Площадь трапеции \(ABCD\) равна произведению полусуммы оснований на высоту.
\(S=\displaystyle\frac{6+10}{2}\cdot3=24\).
Ответ:
24.
































