Условие задачи
22. Постройте график функции \(y=\displaystyle \frac{(\sqrt{16-x^2})^2}{x+4}\) и найдите все значения \(a\), при которых прямая \(y=a\) имеет с графиком данной функции ровно одну общую точку. В ответе запишите наибольшее целое значение \(a\), удовлетворяющее этому условию.
Решение
Данная функция определена, если выражение под корнем неотрицательно, а знаменатель дроби не равен нулю. Получим систему условий:
\(\left\{\begin{matrix} 16-x^2\geq 0, \\ x\neq -4.\end{matrix}\right.\)
Решениея этой системы: \(-4< x< 4\).
При выполнении этого условия формулу функции можно упростить.
\(y=\displaystyle \frac{(\sqrt{16-x^2})^2}{x+4}=\displaystyle \frac{16-x^2}{x+4}=4-x\) при \(-4< x< 4.\)
При других pначениях \(x\) функция не определена. Построим график функции. Это часть прямой \(y=4-x\) при \(-4< x< 4.\)

Если \(x=-4\), то \(y=8.\)
Если \(x= 4\), то \(y=0.\)
Формула \(y=a\) задает горизонтальную прямую. Такая прямая имеет с графиком функции \(y=\displaystyle \frac{(\sqrt{16-x^2})^2}{x+4}\) ровно одну общую точку , если \(0< a< 8.\)
Наибольшее целое решение этого неравенства: \(a=7\).
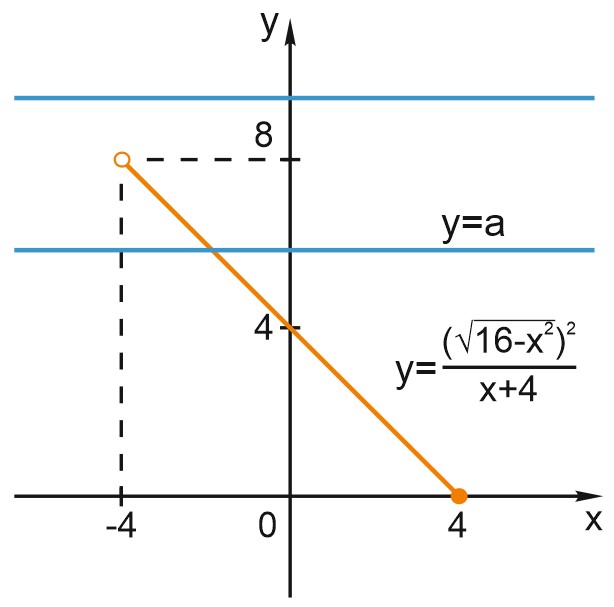
Ответ:
7.
































