Условие задачи
23. Отрезки \(AB\) и \(DC\) лежат на параллельных прямых, а отрезки \(AC\) и \(BD\) пересекаются в точке \(M\). Найдите \(MC\), если \(AB=14, \; DC=56, \; AC=40.\)
Решение
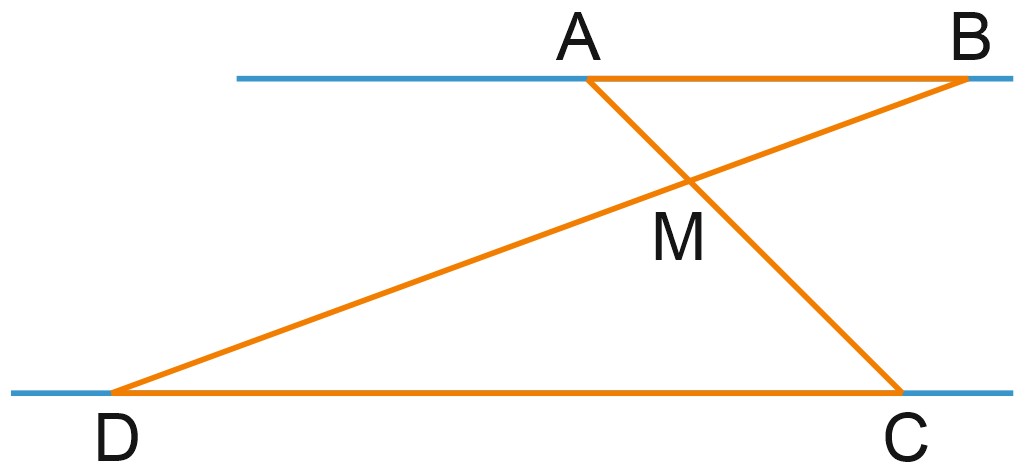
Треугольники \(ABM\) и \(CDM\) подобны по двум углам. Углы \(ABM\) и \(CDM\) в них – накрест лежащие, углы \(AMB\) и \(CMD\) – вертикальные.
Запишем соотношение сходственных сторон: \(\displaystyle \frac{AM}{MC}=\frac{AB}{CD}=\frac{14}{56}=\frac{1}{4}.\)
\(AC=AM+MC=\displaystyle \frac{1}{4}MC+MC=\frac{5}{4}MC\), тогда \(MC=\displaystyle \frac{5}{4}AC, \; AC=32. \)
Ответ:
32.
































