Условие задачи
24. В параллелограмме \(ABCD\) точка \(E\) — середина стороны \(AB\). Известно, что \(EC=ED\). Докажите, что данный параллелограмм — прямоугольник. Каким из полезных фактов вы пользовались при доказательстве? Выберите правильный вариант. В ответе запишите (без точки) номер этого варианта, например: 1
1) Касательная перпендикулярна радиусу, проведенному в точку касания.
2) Если четырехугольник описан вокруг окружности, то суммы длин его противоположных сторон равны.
3) Сумма односторонних углов равна \(180\) градусам.
Решение
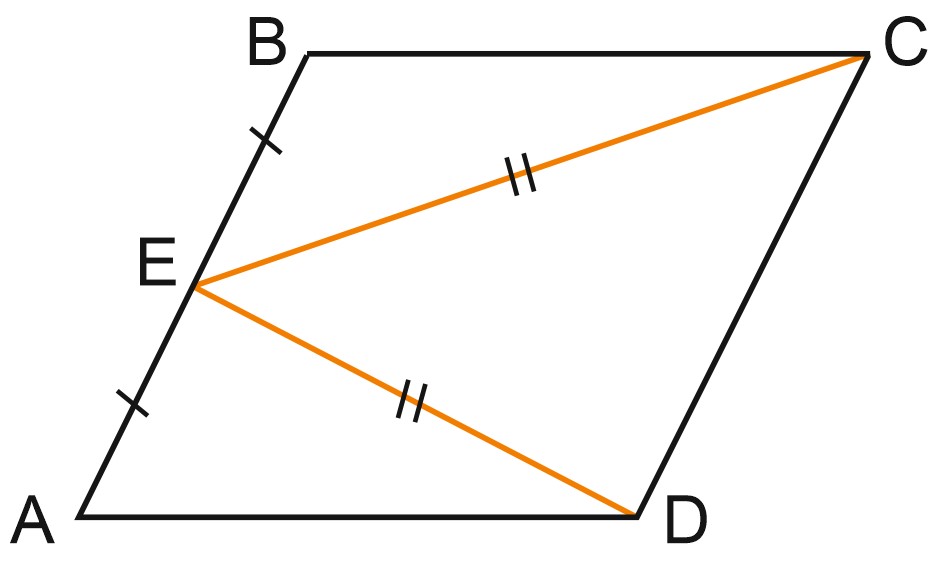
Треугольники \(BEC\) и \(AED\) равны по трем сторонам. Тогда угол \(CBE\) и угол \(DAE\) равны. Эти углы – односторонние, и их сумма равна \(180\) градусов. Значит, углы \(CBE\) и \(DAE\) – прямые, и \(ABCD\) – прямоугольник.
Мы пользовались полезным фактом №3.
Ответ:
3.






























