Условие задачи
Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
Решение
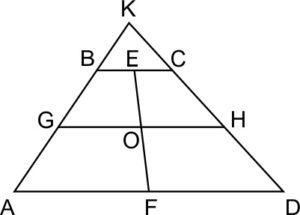
Пусть продолжения боковых сторон трапеции пересекаются в точке К. Поскольку сумма углов А и С равна 90 градусов, угол К – прямой.
Треугольники АКD и ВКС – прямоугольные, КЕ и КF – их медианы, значит, \(KE= \frac{BC}{2}, KF = \frac{AD}{2}, EF = KF - KE = \frac{AD-BC}{2}.\)
Получается, что полуразность оснований трапеции ЕF = 13, а полусумма оснований, то есть средняя линия, GH = 15. Тогда основания трапеции равны 28 и 2.
Ответ:
28 и 2.
































