Условие задачи
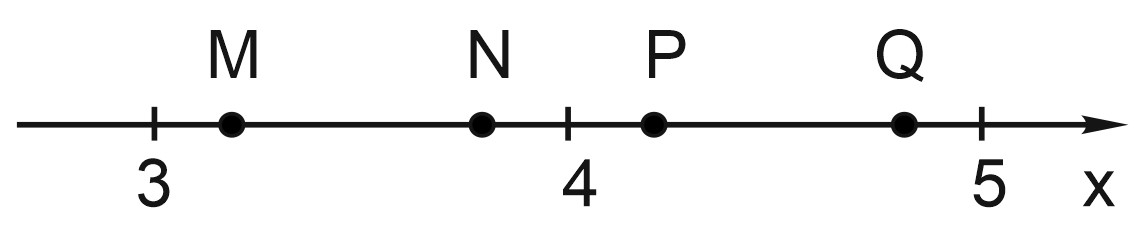
7. Одна из точек, отмеченных на координатной прямой, соответствует числу \(\sqrt{14}\). Какая это точка?
1) точка M;
2) точка N;
3) точка P;
4) точка Q.
Решение
На координатной прямой отмечены целые числа 3, 4, 5. Найдем, между какими целыми числами заключен \(\sqrt{14}.\)
Сравним квадраты чисел 3, 4, 5 и число \((\sqrt{14})^2=14.\)
\(9 < 14 < 16 < 25.\)
Значит, число \(\sqrt{14}\) находится между числами 3 и 4. Это точка \(M\) или точка \(N\). Но точка \(M\) ближе к числу 3, а точка \(N\) ближе к числу 4.
Сравним \(\sqrt{14}\) и \(3,5. \ \sqrt{14}\vee3,5; \ 2\sqrt{14}\vee7.\)
Возведем в квадрат обе части: \(56\vee 49; \ 56 > 49\), значит, \(\sqrt{14} > 3,5.\)
Числу \(\sqrt{14}\) соответствует точка \(N\). Правильный ответ под номером 2.
Ответ:
2.
































