Серединный перпендикуляр к отрезку \(AB\) – это прямая, перпендикулярная отрезку \(AB\) и проходящая через его середину.
Мы построим серединный перпендикуляр, имея только линейку и циркуль. И покажем, как разделить отрезок \(AB\) пополам.
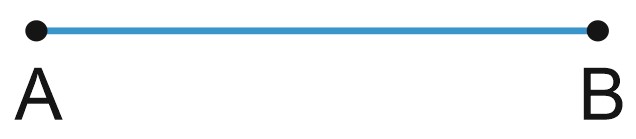
Нарисуем отрезок \(AB\).
Считаем, что на линейке нет делений. С ее помощью можно только проводить прямые линии.
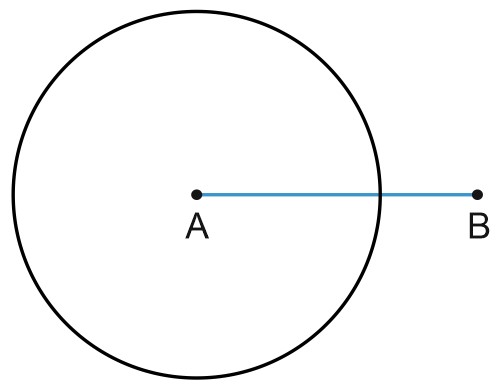
Построим окружность с центром в точке \(A\) и радиусом большим, чем половина отрезка \(AB\).
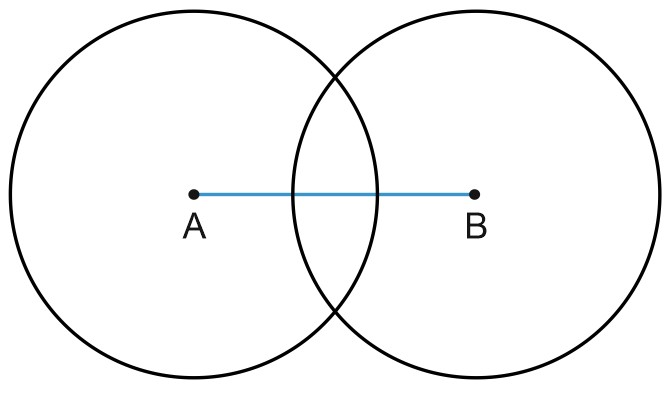
И построим окружность такого же радиуса с центром в точке \(B\).
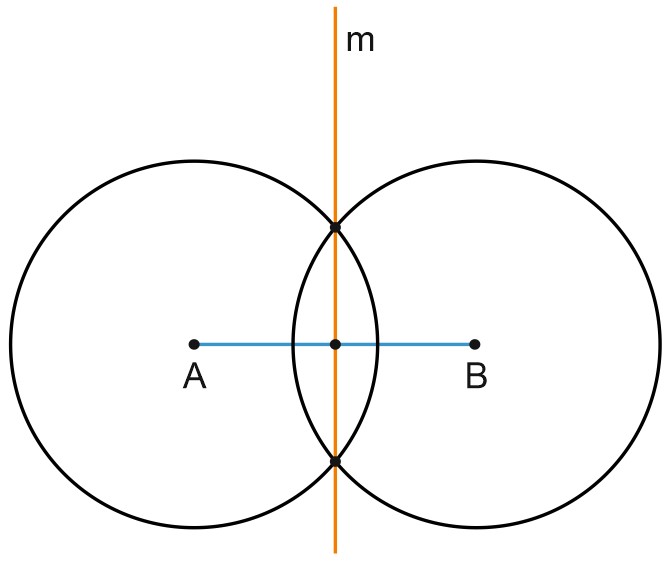
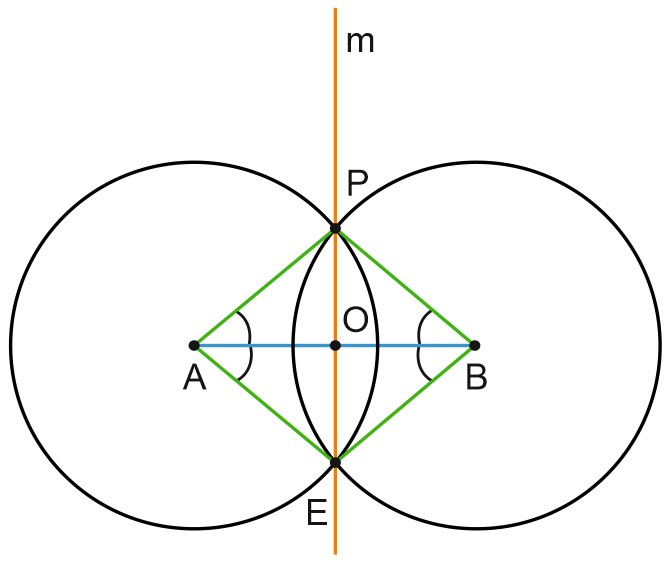
Окружности пересеклись в двух точках. Проведем через точки пересечения окружностей прямую \(m\).
Эта прямая – серединный перпендикуляр к отрезку \(AB\).
В самом деле, пусть \(P\) и \(E\) – точки пересечения окружностей с равными радиусами, с центрами в точках \(A\) и \(B\), \(O\) – точка пересечения \(AB\) и \(PE\). Треугольники \(ABP\) и \(ABE\) равны по трем сторонам. Тогда углы \(OBP\) и \(OBE\) равны, \(BO\) – биссектриса равнобедренного треугольника \(PBE\), и она также является высотой и медианой треугольника \(PBE\). Значит, \(BO\) и \(PE\) перпендикулярны.
Следовательно, \(PO\) перпендикулярна \(AB\), \(PO\) – высота равнобедренного треугольника \(ABP\), и она является также его медианой. \(PE\) – перпендикуляр к \(AB\), проходящий через середину \(AB\), то есть серединный перпендикуляр.
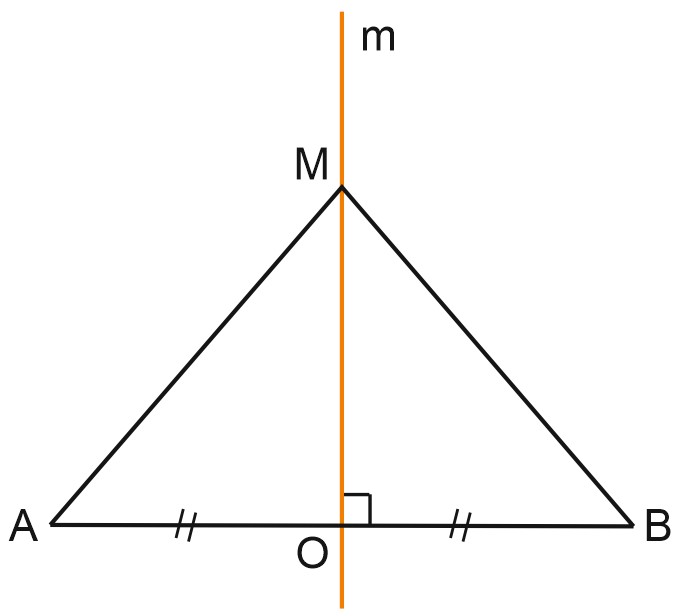
Каждая точка прямой \(m\) одинаково удалена от точек \(A\) и \(B\). Докажем это. Возьмем точку \(M\), лежащую на серединном перпендикуляре к \(AB\).
В треугольнике \(ABM\) медиана \(MO\) является высотой, значит, треугольник \(ABM\) равнобедренный, \(AM=BM\).
Мы доказали, что серединный перпендикуляр к отрезку – это множество точек, равноудаленных от его концов.
Что будет, если в треугольнике провести серединные перпендикуляры ко всем его сторонам? Оказывается, тогда все три вершины треугольника будут лежать на окружности, центр которой – точка пересечения этих серединных перпендикуляров.
Такая окружность называется описанной вокруг треугольника. А сам треугольник – вписанным в окружность.
«Вписанные и описанные треугольники».
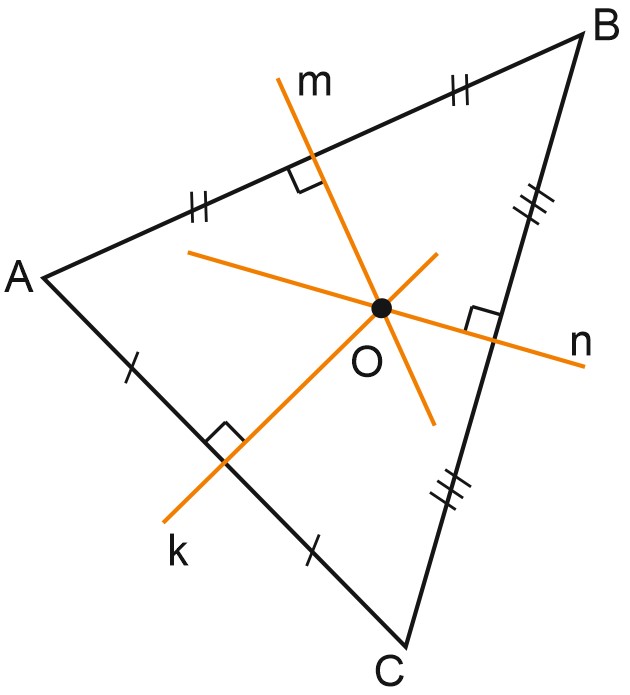
Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, являющейся центром окружности, описанной вокруг треугольника.
Пусть \(m\) – серединный перпендикуляр к стороне \(AB\), \(n\) – серединный перпендикуляр к стороне \(BC\), прямые \(m\) и \(n\) пересекаются в точке \(O\).
Серединный перпендикуляр к отрезку – это множество точек, равноудаленных от его концов.
Точка \(O\) равноудалена от точек \(A\) и \(B\) (поскольку \(O\in m\)), а также от точек \(B\) и \(C\), поскольку \(O\in n\).
Получаем, что точка \(O\) равноудалена также от точек \(A\) и \(C\), то есть \(O\in k\) – серединному перпендикуляру к \(AC\).
Это значит, что три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке. Точка \(O\) равноудалена от \(A\), \(B\) и \(C\) и потому является центром окружности, описанной вокруг треугольника \(ABC\).