В этой теме мы тоже будем строить графики и применять замену переменных.
Рекомендуем повторить темы: определения синуса и косинуса для произвольного угла, основные формулы тригонометрии, простейшие тригонометрические уравнения, часть 1, часть 2.
1. Анна Малкова. При каких значениях параметра \(a\) уравнение \( sin(\pi( \sqrt{a-x^2}-x))=0\) имеет ровно \(2\) решения?
Решение:
Сделав замену: \(\pi( \sqrt{a-x^2}-x)=t\), придем к уравнению \(sint=0\).
Отсюда \(t=\pi k, \; k\in Z\).
Вернемся к переменной \(x\):
\(\pi( \sqrt{a-x^2}-x)=\pi k, \; k\in Z;\)
\(\sqrt{a-x^2}=x+k, \; k\in Z;\)
ОДЗ: \(a-x^2\geq 0. \)
1) Если \(a < 0\), то \(a-x^2 < 0\) – не выполняется условие ОДЗ.
2) Если \(a=0\), то \(\sqrt{-x^2}=x+k, \; k\in Z.\)
Уравнение имеет единственное решение при \(k=0\) и \(x=0\). Это не подходит по условию задачи.
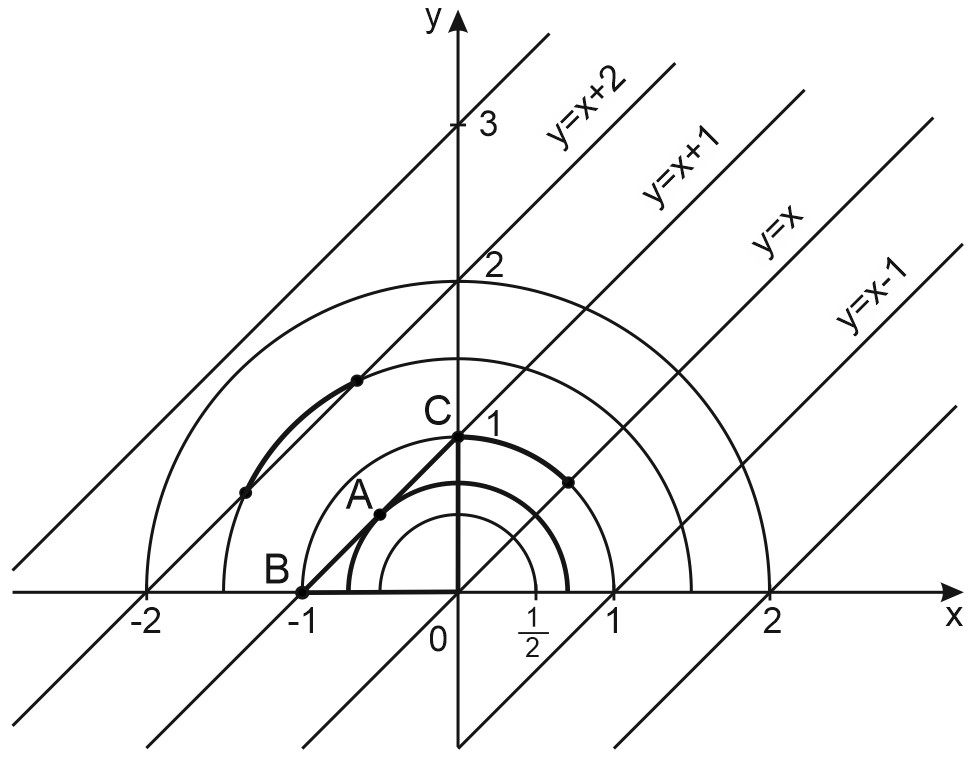
3) Рассмотрим случай \(a > 0\). Пусть \(a=R^2\).
Решим графически уравнение \(\sqrt{R^2-x^2}=x+k, \; k\in Z\).
Построим графики левой и правой частей этого уравнения.
График левой части уравнения \(y=\sqrt{R^2-x^2}\) – верхняя полуокружность с центром в начале координат и радиусом \(R > 0\).
График правой части \(y=x+k\), где \(k\in Z\) – семейство прямых с угловым коэффициентом \(1\).
Чем больше радиус, тем больше параллельных прямых пересекает полуокружность.
Уравнение имеет ровно два решения только в случае, когда полуокружность пересекает прямую \(y=x\) и касается прямой \(y=x+1\) в точке \(A\).
Рассмотрим прямоугольный треугольник \(OBC\). Треугольник равнобедренный, так как \(OC=OB=1\).
\(\angle OCB=\angle OBC=45^\circ\), тогда \(OA\) – медиана и высота, \(OA=R=\displaystyle\frac{\sqrt2}{2}\).
\(a=R^2=\left (\displaystyle\frac{\sqrt2}{2}\right)^2=\displaystyle\frac{1}{2}\).
Если радиус окружности меньше \(\displaystyle\frac{\sqrt2}{2}\), то уравнение имеет единственное решение.
Если радиус окружности больше \(\displaystyle\frac{\sqrt2}{2}\), то уравнение имеет \(3\) и более решений.
Уравнение имеет ровно \(2\) решения при \(a=\displaystyle\frac{1}{2}.\)
Ответ:\(a=\displaystyle\frac{1}{2}.\)
Часто в тригонометрических уравнениях с параметрами применяется эффектная замена переменных.
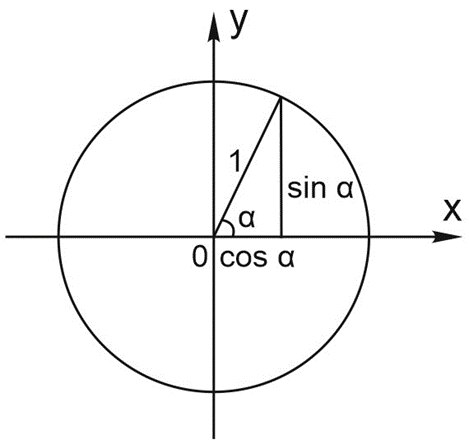
Вспомним определения синуса и косинуса произвольного угла.
- Косинусом угла \(\alpha \) называется абсцисса (то есть координата по оси \(X\)) точки на единичной окружности, соответствующей данному углу \(\alpha \)
- Синусом угла \(\alpha\) называется ордината (то есть координата по оси \(Y\)) точки на единичной окружности, соответствующей данному углу \(\alpha\)
Косинус – абсцисса, то есть координата по \(X\). Синус – ордината, то есть координата по \(Y\). Сейчас вы увидите, как применить эту мощную замену.
2. Найдите все значения параметра \(a\), при каждом из которых уравнение \(2 sin t+cos t=a\) имеет единственное решение на отрезке \(\left [\displaystyle\frac{\pi }{4};\displaystyle\frac{3\pi }{4}\right]\).
Решение:
Сделаем замену: \(cos t=x, \; sin t = y\), в соответствии с определениями косинуса и синуса произвольного угла.
Так как \(cos^2 x+sin^2 x=1\), получим:
\(\left\{\begin{matrix}
2y+x=a, \\
x^2+y^2=1.\end{matrix}\right.\)
При этом \(y\geq \displaystyle\frac{\sqrt{2}}{2}\), так как если \(t\in\left [\displaystyle\frac{\pi }{4};\frac{3\pi }{4} \right ], \; sin t\geq \displaystyle\frac{\sqrt{2}}{2}\).
Система примет вид: \(\left\{\begin{matrix}
y=-\displaystyle \frac{x}{2} +\frac{a}{2},\\
x^2+y^2=1, \\
y\geq \displaystyle \frac{\sqrt{2}}{2}.\end{matrix}\right.\)
Сделаем замену: \(b=\displaystyle\frac{a}{2}\).
Уравнение \(x^2+y^2=1\) задает окружность с центром в начале координат и радиусом \(1\).
Уравнение \(y=-\displaystyle \frac{x}{2}+b\) задает прямую с угловым коэффициентом \(k=-\displaystyle \frac{1}{2}\), сдвинутую на \(b\) по вертикальной оси.
Система \(\left\{\begin{matrix}
x^2+y^2=1,\\
y=-\displaystyle \frac{x}{2}+b, \\
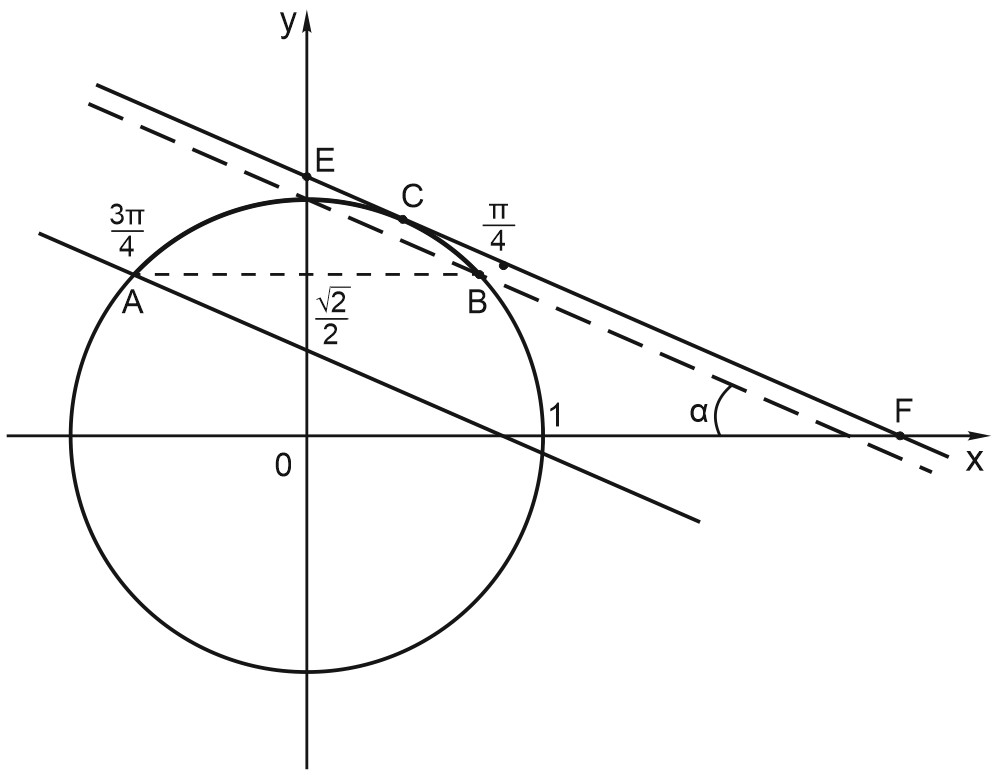
y\geq \displaystyle \frac{\sqrt{2}}{2}\end{matrix}\right. \; \) имеет единственное решение, если прямая \(y=-\displaystyle\frac{x}{2}+b\) пересекает дугу окружности, заданную условиями \(x^2+y^2-1\) и \(y\geq \displaystyle\frac{\sqrt{2}}{2}\) ровно \(1\) раз.
Это происходит в следующих случаях:
1) Прямая проходит через точку \(A \left(-\displaystyle\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2}\right)\). Подставим координаты точки \(A\) в уравнение прямой: \(\displaystyle\frac{\sqrt{2}}{2}=\displaystyle\frac{\sqrt{2}}{4}+b\), отсюда \(b=\displaystyle\frac{\sqrt{2}}{4}\).
2) Прямая проходит выше точки \(A\) и ниже точки \(B\).
Подставив координаты точки \(B \left(\displaystyle \frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2}\right)\) в уравнение прямой, получим: \(b= \displaystyle\frac{3\sqrt{2}}{4}\).
Система имеет единственное решение, если \(\displaystyle\frac{\sqrt{2}}{4}\leq b < \frac{3\sqrt{2}}{4}\), тогда \(\displaystyle\frac{\sqrt{2}}{2}\leq a < \frac{3\sqrt{2}}{2}\).
3) Уравнение также имеет единственное решение в случае касания прямой и дуги окружности в точке \(C\).
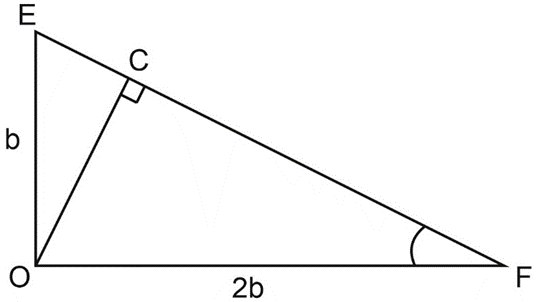
Нарисуем отдельно треугольник \(OEF\).
В треугольнике \(OEF:OE=b, \; tg\angle EFO=\displaystyle\frac{1}{2}\Rightarrow OF=2b, \; OC\) – высота, \(OC=1\).
По теореме Пифагора \(EF=\sqrt{b^2+4b^2}=b\sqrt{5};\)
\(S_{\triangle OEF}=\displaystyle\frac{1}{2}OE\cdot OF=\displaystyle\frac{1}{2}EF\cdot OC;\)
\(2b^2=b\sqrt{5}\), так как \(b\neq 0\), получим: \(b=\displaystyle\frac{\sqrt{5}}{2}\), тогда \(a=\sqrt5\).
Объединив случаи, запишем ответ.
Ответ: \(a\in \left [\displaystyle\frac{\sqrt{2}}{2};\frac{3\sqrt{2}}{2} \right)\cup \{ \sqrt{5}\}.\)
3. При каких значениях параметра \(b\) система
\(\left\{\begin{matrix}
tg t\leq 0, \\
sin t= b cos t -2b+1\end{matrix}\right. \; \) имеет единственное решение?
Решение:
Сделаем замену (стандартную для таких задач): \(cost=x, \; sint=y\).
Получим систему:
\(\left\{\begin{matrix}
\displaystyle \frac{y}{x}\leq 0, \\
x^2+y^2=1, \\
y=bx-2b+1;\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
\displaystyle \frac{y}{x}\leq 0, \\
x^2+y^2=1, \\
y=b(x-2)+1.\end{matrix}\right.\)
Из первого неравенства видно, что \(x\) и \(y\) должны быть разных знаков, причем \(x\neq 0\).
Уравнение \(x^2+y^2=1\) задает окружность с центром в начале координат и радиусом \(1\).
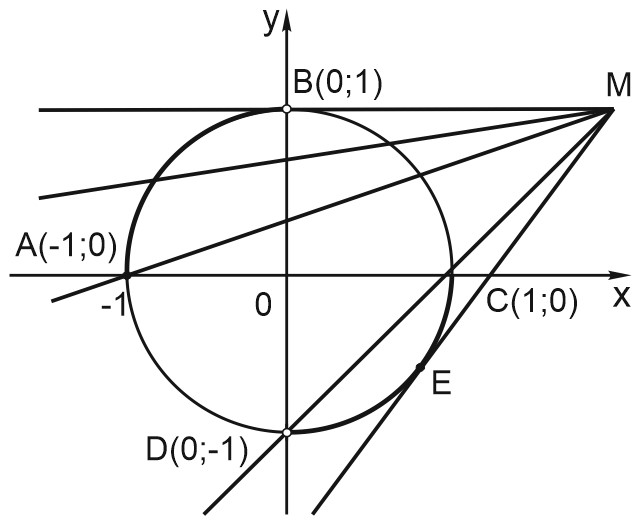
Третье уравнение задает прямую с угловым коэффициентом \(b\) проходящую через точку \(M(2; 1)\).
Решим систему графически:
Система имеет единственное решение в следующих случаях:
1) Если прямая, заданная третьим уравнением, проходит через точку \(A\) или выше точки \(A\) и ниже точки \(B\).
2) В случае касания в точке \(E\).
3) Если прямая проходит через точку \(C(1;0)\).
Рассмотрим по отдельности каждый из этих случаев.
Случай 1. Подставим координаты \(A(-1; 0)\) в уравнение прямой \(y=b(x-2)+1\).
Для точки \(A\): \(b=\displaystyle\frac{1}{3}\).
Для точки \(B\) с координатами \((0; 1)\) получим: \(b=0\).
Знаяит, в первом случае \(b\in \left(0; \displaystyle\frac{1}{3}\right]\).
Случай 2. Найдём значение параметра для прямой, проходящей через точку \(E\) – точку касания.
Вспомним условие касания функции \(y=f(x)\) и прямой \(y=kx+b\).
\(\left\{\begin{matrix}
f(x)=kx+b, \\
f'(x)=k.\end{matrix}\right.\)
Точка \(E\) лежит на нижней полуокружности, уравнение которой можно записать в виде:
\(y=-\sqrt{1-x^2}\).
С учетом условия \(|x|< 1\):
\(\left\{\begin{matrix}
-\sqrt{1-x^2}=b(x-2)+1, \\
\displaystyle \frac{x}{\sqrt{1-x^2}}=b.\end{matrix}\right.\)
Подставим \(b=\displaystyle \frac{x}{\sqrt{1-x^2}}\) в первое уравнение.
\(-\sqrt{1-x^2}=\displaystyle \frac{x(x-2)}{\sqrt{1-x^2}}+1;\)
\(x^2-1=x^2-2x+\sqrt{1-x^2};\)
\(2x-1=\sqrt{1-x^2}.\)
Возведем обе части уравнения в квадрат при условии \(2x-1\geq 0; \; |x| < 1\).
\(1-x^2=4x^2-4x+1;\)
\(5x^2-4x=0;\)
\(x=0\) или \(x=\displaystyle \frac{4}{5}\).
Решение \(x=0\) соответствует точке \(B\), которая тоже является точкой касания прямой и окружности.
Решение \(x=\displaystyle \frac{4}{5}\) соответствует точке \(E\).
При этом \(b=\displaystyle \frac{x}{\sqrt{1-x^2}}=\frac{4}{5}:\sqrt{1-\left (\displaystyle \frac{4}{5}\right )^2}=\displaystyle \frac{4}{5}:\frac{3}{5}=\frac{4}{3}\).
Случай 3. Для точки \(C\) с координатами \((1; 0)\) находим: \(b=1\).
Ответ: \(b\in \left ( 0;\displaystyle \frac{1}{3} \right ]\cup \left\{ 1; \displaystyle \frac{4}{3}\right\}.\)