Анна Малкова
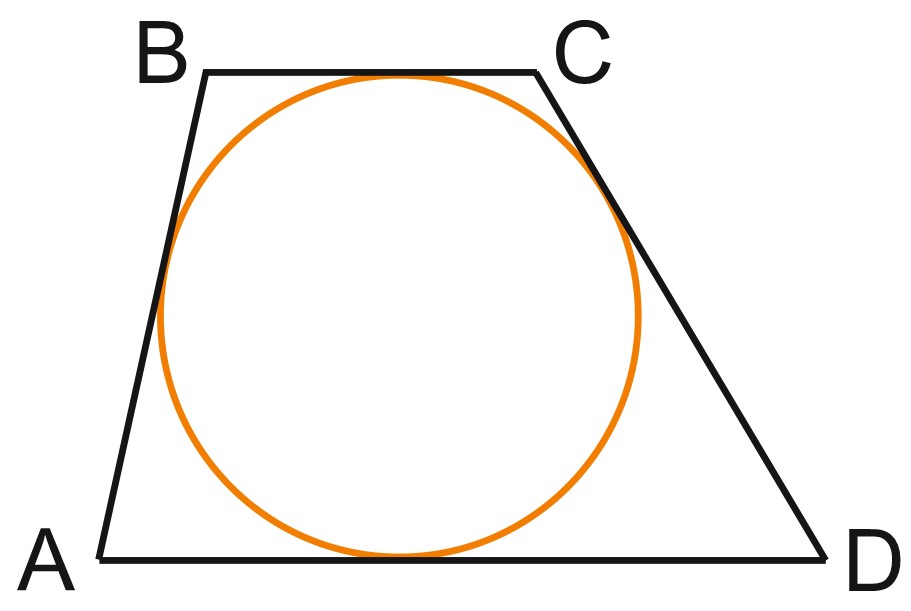
Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны
Доказательство:
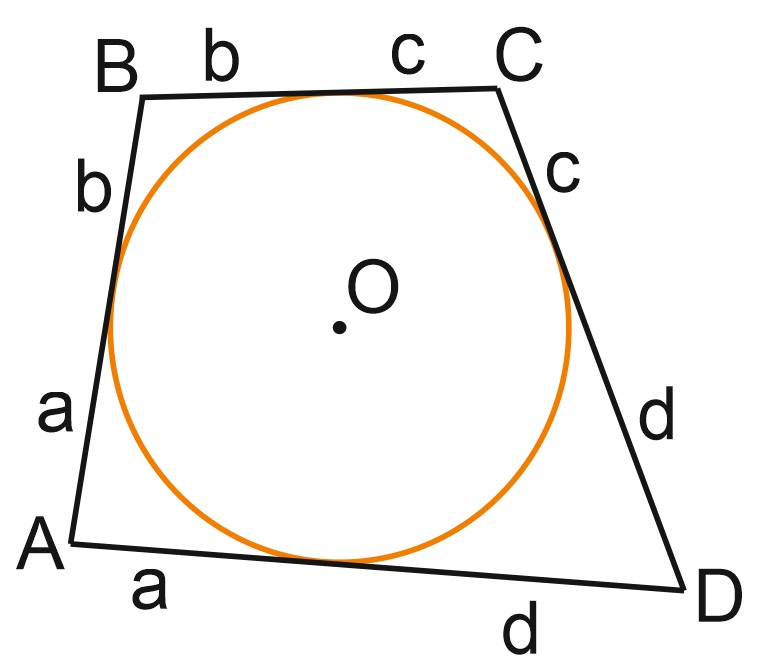
Отрезки касательных, проведенных к окружности из точек \(A, \; B, \; C\) и \(D\), обозначим соответственно \(a, \; b, \; c\) и \(d.\)
Тогда \(AB + CD = AD + BC = a + c = b + d.\)
Докажем обратное утверждение.
Формулируется оно так: Если суммы длин противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Пусть в четырехугольнике \(ABCD\) равны суммы длин противоположных сторон: \(AB + CD = AD + BC.\)
Докажем, что в четырехугольник \(ABCD\) можно вписать окружность.
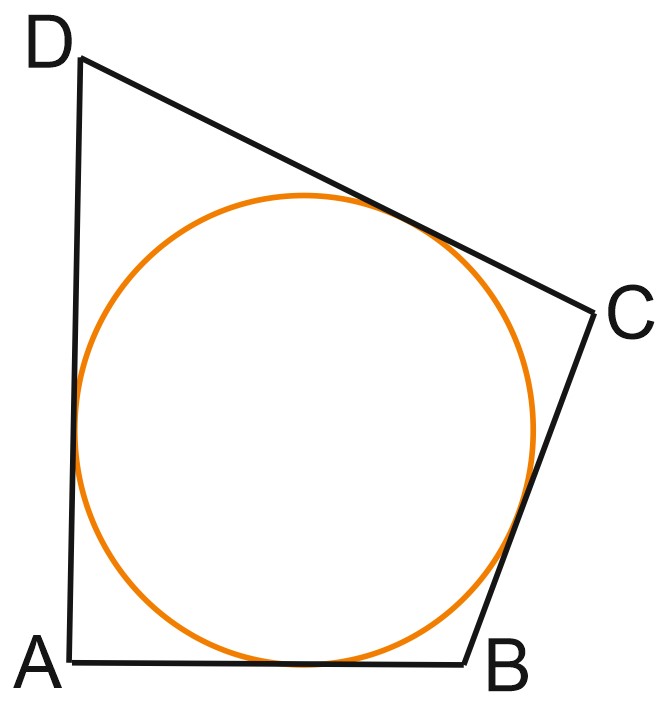
Проведем \(AO\) и \(BO\) – биссектрисы углов \(A\) и \(B, \; AO\cap BO=O.\)
Точка \(O\) равноудалена от сторон \(AB, \; BC\) и \(AD\) четырёхугольника \(ABCD\). Окружность с центром \(O\) касается сторон \(AB, \; BC\) и \(AD\) четырехугольника.
Покажем, что окружность с центром в точке \(O\) касается также стороны \(CD\), то есть вписана в четырёхугольник \(ABCD\).
Предположим, что это не так, и \(CD\) либо не имеет общих точек с окружностью, либо является секущей.
Рассмотрим первый случай. Проведем касательную \(C_1D_1\) параллельно \(CD\).
Четырехугольник \(ABC_1D_1\) – описанный вокруг окружности, и для него выполняется равенство:
\(AB+C_1D_1=AD_1+BC_1.\)
При этом \(BC_1=BC-CC_1,\, \, \, AD_1=AD-DD_1\). Получим:
\(AB+C_1D_1=AD-DD_1+BC-CC_1;\)
\(AD+BC-AB=C_1D_1+CC_1+DD_1.\)
С другой стороны,
\(AB+CD=AD+BC,\) поэтому
\(AD+BC-AB=CD\) и \(CD=C_1D_1+CC_1+DD_1.\)
Получили, что для четырехугольника \(CDD_1C_1\) длина стороны \(CD\) равна сумме трех других сторон. Это невозможно. Мы пришли к противоречию. Предположение о том, что \(CD\) не имеет общих точек с окружностью, было неверно.
Аналогично доказывается, что \(CD\) не может быть секущей к окружности. Значит, \(CD\) – касательная к окружности и четырехугольник \(ABCD\) – описанный вокруг окружности.
Задачи ЕГЭ по теме «Описанный четырехугольник»
1. В четырёхугольник \(ABCD\) вписана окружность, \(AB=10, \; CD=16\). Найдите периметр четырёхугольника \(ABCD\).
Решение:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
Значит, \(AD+BC=AB+DC=10+16=26. \)
Тогда периметр четырехугольника равен \(AD+BC+ AB +DC =26\cdot 2=52.\)
1) Площадь описанного четырехугольника равна произведению полупериметра четырёхугольника на радиус вписанной в него окружности.
\(\displaystyle S=\frac{a+b+c+d}{2}\cdot r=pr.\)
2) Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
3) В любой ромб можно вписать окружность.
4) В любой квадрат можно вписать окружность.
5) В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом.
6) В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
7) В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон равна сумме длин оснований.
\(c+d=a+b.\)
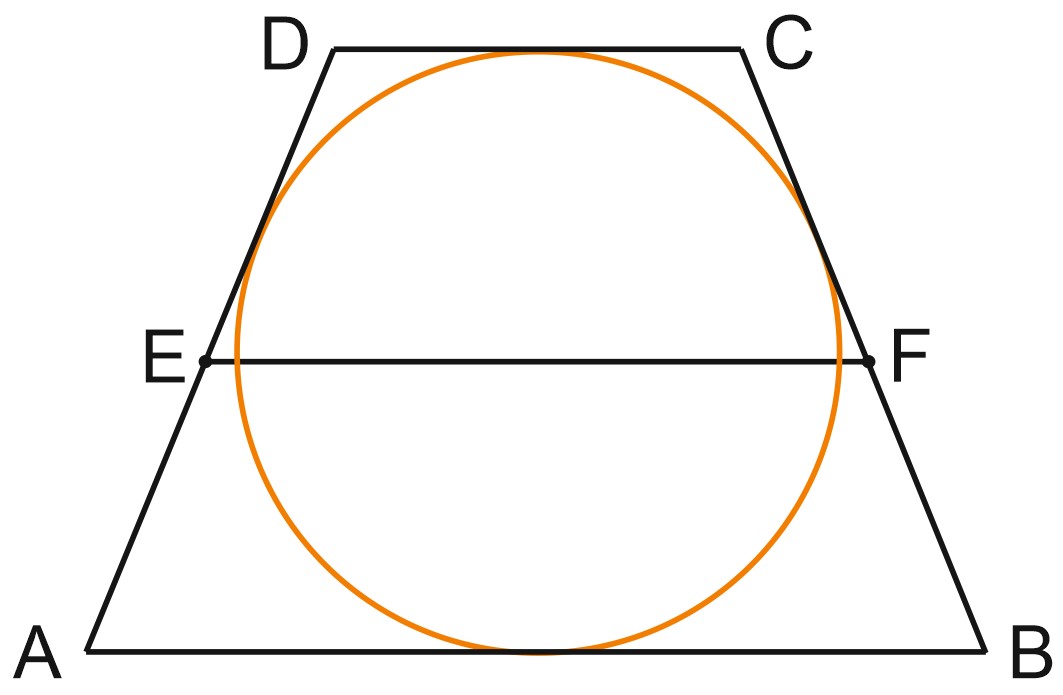
8) Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна ее средней линии
Доказательство:
Поскольку трапеция описана вокруг окружности, \(AB + CD = AD + BC = 2 BC\), отсюда \(BC=\displaystyle \frac{AB+CD}{2}\) – то есть средней линии трапеции; \(BC = EF.\)
2. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как \(1:2:3\). Найдите большую сторону этого четырехугольника, если известно, что его периметр равен \(32\).
Решение:
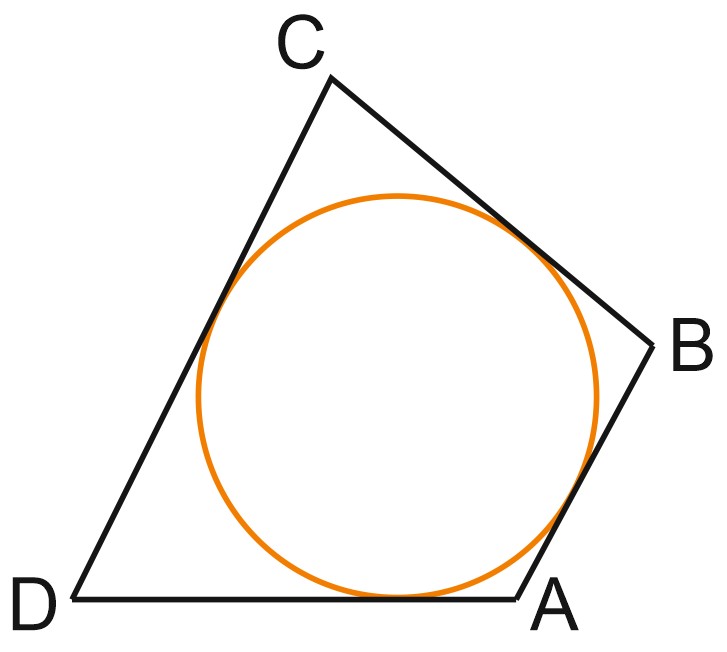
Пусть сторона \(AB\) равна \(x, \; AD\) равна \(2x\), а \(DC - 3x\).
По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит, \(x+3x=BC + 2x.\)
Получается, что \(BC\) равна \(2x\). Тогда периметр четырехугольника равен \(8x\). Мы получаем, что \(x=4\), а большая сторона равна \(12\).
Ответ: 12.
3. Около окружности описана трапеция, периметр которой равен \(40\). Найдите ее среднюю линию.
Решение:
Мы помним, что средняя линия трапеции равна полусумме оснований.
Пусть основания трапеции равны \(a\) и \(c\), а боковые стороны — \(b\) и \(d\).
По свойству описанного четырехугольника, \(a+c=b+d\), и значит, периметр равен \(2\left( a+c \right).\)
Получаем, что \(a+c=20\), а средняя линия равна \(10\).
Ответ: 10.
4. Найдите радиус окружности, вписанной в квадрат со стороной \(16\).
Решение:
Радиус окружности, вписанной в квадрат, равен половине его стороны. Поэтому \(r = 8.\)
Ответ: 8.
5. Периметр прямоугольной трапеции, описанной около окружности, равен \(22\), ее большая боковая сторона равна \(7\). Найдите радиус окружности.
Решение:
Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна \(11\) (половине периметра).
Боковая сторона \(CB = 7,\) тогда боковая сторона \(AD = 11-7 = 4.\)
Радиус вписанной окружности равен половине \(AD,\) т. е. \(2\).
Ответ: 2.
6. Найдите высоту трапеции, в которую вписана окружность радиуса \(14\).
Решение:
Высота трапеции, в которую вписана окружность, равна диаметру этой окружности: \(2\cdot 14=28.\)
Ответ: 28.
7. Боковые стороны трапеции, описанной около окружности, равны \(19\) и \(13\). Найдите среднюю линию трапеции.
Решение:
Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна \(19+13=32.\)
Средняя линия трапеции равна полусумме оснований \(32:2=16.\)
Ответ: 16.
8. Около окружности, радиус которой равен \(2\), описан многоугольник, периметр которого равен \(16\). Найдите его площадь.
Решение:
Площадь описанного многоугольника можно найти как произведение полупериметра на радиус вписанной окружности: \(S=pr=8\cdot 2=16.\)
Ответ: 16.
9. В равнобедренной трапеции, вписанной в окружность, диагонали взаимно перпендикулярны. Средняя линия трапеции равна \(12\). Найти радиус вписанной окружности.
Решение:
Радиус окружности, вписанной в трапецию, равен половине ее высоты.
Рассмотрим равнобедренную трапецию \(ABCD, \; AC\perp BD.\)
Проведем \(CK\parallel BD.\)
Треугольник \(ACK\) – прямоугольный (с прямым углом \(C\)) и равнобедренный. Его гипотенуза \(AK\) равна сумме оснований трапеции (т. к. \(BCKD\) – параллелограмм, и \(BC = KD\)), \(2\cdot 12= 24.\)
Высота трапеции \(CH\) является также высотой и медианой, проведенной из прямого угла равнобедренного прямоугольного треугольника \(ACK\).
\(CH = AK:2 = 12.\)
Радиус вписанной окружности \(r = CH:2 = 6.\)
Ответ: 6.
10. В четырёхугольник \(ABCD\) можно вписать и вокруг него можно описать окружность. Диагонали этого четырёхугольника перпендикулярны. Найдите его площадь, если радиус описанной окружности равен \(5\), а \(AB=2BC.\)
Решение:
Обозначим \(BC=x\). Тогда \(AB=2x.\)
Обозначим также \(CD=z, \; AD=y.\)
Вписать окружность в четырехугольник можно тогда и только тогда, когда суммы длин противоположных сторон четырехугольника равны.
Значит, \(x+y=2x+z.\) Отсюда \(y=x+z.\)
Пусть \(O\) – точка пересечения диагоналей четырёхугольника \(ABCD.\)
При пересечении \(AC\) и \(BD\) образуется четыре прямоугольных треугольника. Это \(\triangle AOB, \; \triangle COB, \; \triangle COD, \; \triangle AOD.\)
Пусть \(AO=a, \; BO=b, \; CO=c, \; DO=d.\)
Запишем для каждого из этих треугольников теорему Пифагора:
Из \(\triangle AOB: \; 4x^{2}=a^{2}+b^{2}.\)
Из \(\triangle BOC: \; x^{2}=b^{2}+c^{2}.\)
Из \(\triangle COD: \; z^{2}=c^{2}+d^{2}.\)
Из \(\triangle AOD: \; y^{2}=a^{2}+d^{2}.\)
Мы получили систему уравнений.
Сложив первое и третье из них и выразив \(x^{2}+y^{2}\) как \(a^{2}+b^{2}+c^{2}+d^{2},\) получим: \(4x^{2}+z^{2}=x^{2}+y^{2}.\)
Кроме того, \(y=x+z.\) Это мы нашли в самом начале.
Из системы уравнений
\(\begin{cases}
3x^{2}+z^{2}=y^{2}, \\
y=x+z
\end{cases}\)
находим: \(y=2x, \; z=x.\)
Значит, \(AD=AB, \; CD=BC.\)
Перестроим чертеж. Это надо сделать обязательно. Появились новые данные – рисуем новый чертеж. По условию, четырехугольник \(ABCD\) вписан в окружность.
Треугольники \(ABC\) и \(ADC\) равны по трем сторонам. Значит, углы \(ABC\) и \(ADC\) равны.
Четырехугольник \(ABCD\) вписан в окружность, поэтому сумма углов \(ABC\) и \(ADC\) равна \(180\) градусов. Мы получили, что углы \(ABC\) и \(ADC\) – прямые. Тогда \(AC\) – диаметр окружности.
По условию, \(R=5\), тогда \(AC=10.\)
\(\angle CAB\) опирается на диаметр.
\(\triangle ACB\) – прямоугольный, \(AC\) – его гипотенуза.
По теореме Пифагора для \(\triangle ACB\):
\(100=x^{2}+4x^{2}.\)
Отсюда \(x^{2}=20.\)
\(S_{ABCD}=2\cdot S_{\triangle ABC}=2x^{2}=40.\)
Ответ: 40.