Анна Малкова
Это продолжение тем «Сумма и произведение событий» и «Дерево возможных исходов».
1. У Дениса в пенале 6 ручек, из которых 3 пишут, а 3 другие – нет. В начале урока он случайным образом выбирает ручку из пенала. Найдите вероятность того, что пишущая ручка ему попадётся со второй попытки. При этом считаем, что, если ему попадается непишущая ручка, он её откладывает в сторону.
Решение:
По условию задачи, первая ручка, которую выбрал Денис, не пишет, а вторая пишет.
Первая ручка не пишет с вероятностью \(p_1=\displaystyle \frac{3}{6}=0,5=\frac{1}{2}\).
После того, как Денис ее вытащил, осталось 5 ручек, из которых 3 пишут;
Вероятность вытащить пишущую ручку \(p_2=\displaystyle \frac{3}{5}\).
Вероятность и того, и другого события равна \(p_{1}\cdot p_{2}=\displaystyle \frac{1}{2}\cdot\frac{3}{5}=0,3\).
Ответ: 0,3.
2. Известно, что в семье Петровых четверо детей. Найдите вероятность того, что ровно трое из четырех детей – девочки. Вероятности рождения мальчика или девочки считаем одинаковыми.
Решение:
Выпишем возможные исходы, условно обозначив событие «родилась девочка» цифрой 0, а событие «родился мальчик» цифрой 1.
Получим следующие комбинации:
0000
0001
0010
0011
0100
0101
0110
0111…
…
1111
- всего 16 вариантов.
Из них только 4 благоприятных исхода:
0001, 0010, 0100, 1000.
Ответ: 0,25
3. ЕГЭ. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Решение:
Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?
Можно воспользоваться формулами комбинаторики. Однако есть более простое решение.
Кодируем монеты числами 1, 2 (это пятирублёвые), 3, 4, 5, 6 (это десятирублёвые). Условие задачи можно теперь сформулировать так:
Есть шесть фишек с номерами от 1 до 6. Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами 1 и 2 не оказались вместе?
Давайте запишем, что у нас в первом кармане.
Для этого составим все возможные комбинации из набора 123456. Набор из трёх фишек будет трёхзначным числом. Очевидно, что в условиях задачи 123 и 231 — это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:
123, 124, 125, 126…
Следующее число 134 (поскольку мы располагаем числа по возрастанию), а затем 135, 136, 145, 146, 156. Мы перебрали все возможные комбинации, начинающиеся с цифры 1. Продолжаем: 234, 235, 236, 245, 246, 256, 345, 346, 356, 456, всего 20 возможных исходов.
По условию, фишки с номерами 1 и 2 не должны оказаться вместе. Это значит, например, что комбинация 356 нам не подходит — она означает, что фишки 1 и 2 обе оказались в не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только 1, либо только 2. Вот они:
134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего 12 благоприятных исходов.
Тогда искомая вероятность равна \(\displaystyle \frac{12}{20}=0,6\).
Ответ: 0,6.
4. Статистика показывает, что 5% автомобилей имеют неисправные тормоза. Если остановить 3 автомобиля и проверить их техническое состояние, то какова вероятность того, что среди них будет хотя бы один автомобиль с неисправными тормозами? Ответ округлите до тысячных.
Решение:
С вероятностью 0,95 случайно выбранный автомобиль имеет исправные тормоза.
У трех случайно выбранных автомобилей исправные тормоза с вероятностью \(p_1 = 0,95^3\).
А неисправные хотя бы у одного из них – с вероятностью \(1 - p_1= 1 - 0,95^3\approx 0,143\).
Ответ: 0,143
5. Татьяна Сиротина. Баскетболист пробивает три штрафных броска. Вероятность попадания при первом, втором и третьем бросках равна соответственно 0,8, 0,6 и 0,3. Найдите вероятность того, что мяч залетит в кольцо ровно два раза.
Решение:
Вероятность попадания при первом броске равна 0,8. Значит, вероятность промаха равна \(1-0,8=0,2\).
Аналогично, при втором броске вероятность промаха равна \(1-0,6=0,4\). При третьем броске вероятность промаха равна 0,7.
Считаем, что результат каждого броска не зависит от промаха или попадания при предыдущем броске.
Вероятность события «попал ровно два раза» равна \(0,8\cdot 0,6\cdot 0,7+0,8\cdot 0,4\cdot 0,3+0,2\cdot 0,6\cdot 0,3=0,336+0,096+0,036=0,468\).
Ответ: 0,468.
6. ЕГЭ. Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца?
Решение:
Вероятность получения новой принцессы равна \(\displaystyle \frac{8}{10}\), а вероятность противоположного события – получение «старой» принцессы – равна \(\displaystyle \frac{2}{10}\). Вероятность того, что для получения следующей принцессы Маше придётся купить 2 шоколадных яйца, равна \(\displaystyle \frac{2}{10}\cdot\frac{8}{10}=0,16\) (в первом яйце «старая» принцесса, во втором новая).
Вероятность того, что для получения следующей принцессы Маше придётся купить 3 шоколадных яйца, равна \(\displaystyle \frac{2}{10}\cdot\frac{2}{10}\cdot\frac{8}{10}=0,032\). Вероятность получить новую принцессу из второго или третьего яйца \(0,16+0,032=0,192\).
Ответ: 0,192.
7. ЕГЭ. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 69 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 69 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент А. получит не менее 69 баллов по математике, равна 0,6, по русскому языку — 0,6, по иностранному языку — 0,6 и по обществознанию — 0,9.
Найдите вероятность того, что А. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение:
Для того, чтобы поступить хотя бы на одну из этих специальностей, необходимо сдать и русский, и математику не менее чем на 69 баллов.
События «сдать ЕГЭ по математике не ниже, чем на 69 баллов» и «сдать ЕГЭ по русскому языку не ниже, чем на 69 баллов» независимы. Вероятность их произведения (то есть наступления и того, и другого события) равна произведению их вероятностей:
\(P_1=0,6\cdot 0,6=0,36\).
Помимо этого, нужно сдать иностранный язык (И) или обществознание (О) не менее, чем на 69 баллов. Обозначим вероятность этого события \(P_2\).
События «сдать ЕГЭ по иностранному не ниже, чем на 69 баллов» и «сдать ЕГЭ по обществознанию не ниже, чем на 69 баллов» совместны – то есть может произойти и то, и другое.
Поэтому вероятность события «сдать не ниже 69 баллов ЕГЭ по иностранному или по обществознанию» \(P_2=\)\(P(И)+P(О)-P(И\cdot О)\)\(=0,6+0,9-0,54=0,9+0,06=0,96\).
Вероятность того, что набраны баллы для поступления или на специальность «Лингвистика», или на специальность «Коммерция», или на обе этих специальности, равна \(P_1 \cdot P_2=0,36 \cdot 0,96=0,3456\).
Ответ: 0,3456.
8. ЕГЭ. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение:
Вероятность того, что кофе в автомате остался к концу дня, обозначим «плюсом». Вероятность того, что кофе в автомате закончился – «минусом».
Вероятность того, что кофе закончился, равна 0,3 и для одного, и для другого автомата.
+ -
I автомат 0,7 0,3
II автомат 0,7 0,3
Но что мы видим? Вероятность того, что кофе закончился в обоих автоматах, равна не 0,09, как мы могли бы предположить, а 0,12 - по условию задачи.
В чем же дело?
Если кофе закончился в одном автомате, значит, все, кто хочет кофе, пойдут по второму, и в нем кофе выпьют уже быстрее. Получается, что события «кофе закончился в первом автомате» и «кофе закончился во втором» являются зависимыми, и вероятность произведения этих событий считается уже по-другому.
Найдем вероятность того, что кофе закончится хотя бы в одном из автоматов. Он может закончиться в первом, во втором или в обоих сразу, и тогда, чтобы найти вероятность того, что кофе останется в обоих, мы из единицы вычтем вероятность того, что кофе закончился хотя бы в одном из автоматов.
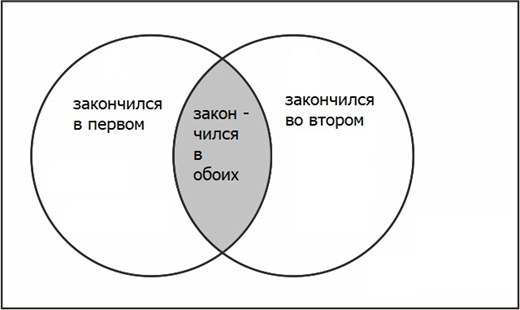
Вероятность того, что кофе закончится хотя бы в одном автомате, равна сумме вероятностей того, что кофе закончится в первом автомате, плюс вероятность того, что кофе закончился во втором, минус вероятность того, что кофе закончится в обоих автоматах сразу.
Так же мы считали бы площадь фигуры на данном рисунке. Мы бы сложили площадь первого круга и площадь второго, а затем вычли площадь их пересечения, поскольку она посчитана дважды.
Вероятность того, что кофе закончится хотя бы в одном автомате:
\(P_1=0,3+0,3-0,12=0,48\).
Тогда вероятность того, что кофе останется в обоих автоматах
\(P_2=1-0,48=0,52\).
Ответ: 0,52.
9. ЕГЭ. Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на игровые пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определён жребием. Всего в турнире участвует 16 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга – Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом?
Решение:
Есть длинный способ решения этой задачи. Либо Иван и Алексей встретились в первом туре. Либо они не встретились в первом туре и каждый из них выиграл в первом туре и они встретились во втором туре. Либо они не встретились в первом туре, и каждый из них выиграл в первом. И не встретились во втором туре, и каждый из них выиграл во втором. И они встретились в третьем туре. Либо… но чтобы описать встречу в четвертом туре, нужно построить очень длинное предложение : -)
Мы поступим проще: посчитаем вероятность по определению.
Найдем, сколько всего можно составить пар из 16 игроков. Те, кто изучал комбинаторику, знают, что это количество равно числу сочетаний из 16 по 2. Но можно посчитать и без формулы.
Присвоим игрокам номера от 1 до 16. Первый игрок может сыграть со вторым, третьим и всеми остальными. Получим пары: 1-2; 1-3… 1-16, всего 15 пар.
Для второго игрока 14 пар. Это 2-3; 2-4… 2-16. Ясно, что пара 2-1 – это то же самое, что пара 1-2, порядок элементов в паре не важен.
Для третьего игрока 13 пар, 3-4; 3-5… 3-16. Рассуждая подобным образом, получим, что для четвертого игрока 12 пар, для пятого 11… для 15-го игрока 1 пара, 15-16.
Общее количество пар равно \(15 + 14 + 13… + 2 + 1 = 120\), посчитали по формуле суммы арифметической прогрессии. Значит, общее количество исходов равно 120.
Но по правилам турнира, играют только 15 пар. В первом туре 8, во втором 4, в третьем 3 и в четвертом одна, \(8 + 4 + 2 + 1 = 15\). Количество благоприятных исходов (возможностей встретиться Ивану и Алексею в одной паре) равно 15. Находим вероятность по определению,
\(p = 15 : 120 = 0,125\).
Ответ: 0,125.
10. Татьяна Сиротина. У Пятачка есть три воздушных шарика: синий, зеленый и желтый.
Винни-Пух просит у него синий шарик и за это обещает угостить мёдом. Ослик Иа хочет зеленый и за это обещает спеть песенку, причем шарики других цветов Пуху и Ослику не подойдут. Кролик готов сказать «спасибо» за шарик любого цвета.
Известно, что Винни-Пух с вероятностью 0,7 сам съест весь мёд, а ослик Иа с вероятностью 0,4 не захочет петь, получив шарик. Пятачок отправил по почте каждому из друзей по шарику, но при этом забыл, кому какого цвета нужен шарик. Найдите вероятность, того, что все друзья Пятачка выполнят свои обещания.
Решение:
Кролик скажет Пятачку «спасибо» в любом случае. Остаются Винни-Пух и Иа. Они выполнят свои обещания только в том случае, если Винни-Пух получит синий шарик, ослик Иа – зеленый. Пятачок забыл, кому какой шарик нужен, поэтому возможных исходов всего 6. Покажем их, обозначив зеленый, синий и желтый шарики буквами З, С и Ж.
Ослик Иа Винни-Пух Кролик
З С Ж
З Ж С
Ж З С
Ж С З
С Ж З
С З Ж
Благоприятный исход только один (первый в таблице). Вероятность того, что друзья Пуха получат шарики нужного цвета, равна \(\displaystyle \frac{1}{6}\).
Правда, Винни-Пух сам съест весь мёд с вероятностью 0,7 (а не съест с вероятностью \(1-0,7=0,3\)). Ослик Иа после получения зеленого шарика захочет спеть с вероятностью \(1-0,4=0,6\). Значит, вероятность того, что у друзья Пятачка получат шарики нужного цвета, и при этом Винни-Пух угостит Пятачка мёдом, а ослик Иа споет песню (независимые события) равна \(\displaystyle\frac{1}{6}\cdot 0,3\cdot 0,6=0,03\).
Ответ: 0,03.
11. ЕГЭ. В ресторане «Шеш-беш» администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно 2 игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Решение:
Ресторан «Шеш-Беш» должен сказать составителям задачи спасибо за такую рекламу : -)
Заметим, что условие не вполне корректно. Например, я бросаю кости и при первом броске получаю 5 и 6 очков. Надо ли мне бросать второй раз? Могу ли я получить 2 десерта, если дважды выброшу комбинацию из 5 и 6 очков?
Уточним условие. Если при первом броске получилась комбинация из 5 и 6 очков, то больше кости я не бросаю и забираю свой десерт (или кофе).
Если первый раз не получилось – у меня есть вторая попытка.
Решим задачу с учетом этих условий.
При броске одной игральной кости возможны 6 исходов, при броске 2 костей 36 исходов. Только два из них благоприятны: это 5; 6 и 6; 5, вероятность каждого из них равна \(\displaystyle \frac{1}{36}\). Вероятность выбросить 5 и 6 при первом броске равна \(\displaystyle \frac{1}{36}+\frac{1}{36}=\frac{2}{36}=\frac{1}{18}\).
Вероятность того, что с первой попытки не получилось, равна \(1-\displaystyle \frac{1}{18}=\frac{17}{18}\).
Если в первый раз не получилось выбросить 5 и 6, а во второй раз получилось – вероятность этого события равна \(\displaystyle \frac{17}{18}\cdot\frac{1}{18}\).
Вероятность выбросить 5 и 6 с первой или со второй попытки равна \(\displaystyle \frac{1}{18}\left (1+\frac{17}{18}\right)=\frac{35}{324}\approx 0,11\).
Ответ: 0,11.
12. Ведущий конкурса предлагает троим участникам задумать любую цифру от 0 до 9. Считая, что выбор каждым из участников любой цифры равновероятен, найти вероятность того, что у кого-то из них задуманные цифры совпадут.
Решение:
Запишем возможные исходы в виде упорядоченных троек чисел, которые задумали первый, второй и третий участники. Благоприятные для нас исходы – когда хотя бы 2 цифры совпадают.
Всего, очевидно, \(10^3 = 1000\) возможных исходов.
Рассмотрим случаи, когда первый задумал цифру 0.
(0, 0,0) (0,0, 1) (0, 0, 2) … (0, 0, 9) – 10 исходов, все благоприятные (две цифры 0)
(0, 1, 0) (0, 1, 1) (0, 1, 2) … (0, 1, 9) – 10 исходов, из них 2 благоприятных: (0, 1, 0) и (0, 1, 1).
(0, 2, 0) (0, 2, 1) (0, 2, 2) … (0, 2, 9) – 10 исходов, 2 благоприятных.
Аналогично, для случаев, когда первый задумал 0, а второй – цифру от 3 до 9, получаем по 2 благоприятных исхода из 10, всего \(10+2 \cdot 9=28\) благоприятных исходов.
Для случаев, когда первый задумал цифру от 1 до 9, также получаем по 28 благоприятных исходов. Значит, всего 280 благоприятных исходов из 1000 возможных.
\(p=\displaystyle \frac{280}{1000}=0,28.\)
Ответ: 0,28
13. Преподаватель пригласил на собеседование трех из отстающих студентов через старосту группы. Староста забыл фамилии приглашенных и направил случайно трех из шести отстающих. Какова вероятность того, что это были нужные преподавателю студенты?
Решение:
Сколько способов выбрать 3 студентов из 6? (неупорядоченные тройки).
Обозначим студентов: 1, 2, 3, 4, 5, 6.
Возможные тройки:
123, 124, 125, 126, 134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 345, 346, 356, 456, 256.
Всего 20 троек \(=C_{6}^{3}\).
Вероятность выбрать нужную тройку равна \(\displaystyle \frac{1}{20}=0,05\).
Ответ: 0,05
14. Анна Малкова. Найдите вероятность того, что при броске трех игральных кубиков только на двух из них количество очков будет одинаковым (а на третьем – другое, например, 414). Ответ округлите до сотых.
Решение:
Всего будет \(6^3 = 216\) вариантов.
Рассмотрим вариант ААВ. Здесь А – одна из 6 цифр от 1 до 6, В – одна из 5 цифр (поскольку не равна А).
Цифра В может стоять на первом, втором или третьем месте, то есть возможны 3 варианта: ААВ, АВА, ВАА. Значит, для каждой цифры А всего получится 15 вариантов (5 вариантов для цифры В, и стоять она может на одном из 3 мест).
Поскольку А принимает значения от 1 до 6, всего имеем 90 вариантов.
\(p=\displaystyle \frac{9}{216}\approx 0,42\).
Ответ: 0,42.
15. ЕГЭ. Игральную кость бросают до тех пор, пока сумма всех выпавших очков не превысит число 3. Какова вероятность того, что для этого потребуется ровно 3 броска? Ответ округлите до сотых.
Решение:
Кажется, что задача сложная (на самом деле нет).
Давайте подумаем: как получилось, что ровно за 3 броска игральной кости сумма выпавших очков оказалась больше трех? Из этого следует, что за 2 броска сумма выпавших очков была меньше 3 или равна 3.
Если за 2 броска сумма выпавших очков была меньше 3, значит, она была равна 2, то есть первый раз выпала единица и второй раз тоже единица. Вероятность этого события равна \(\displaystyle \frac{1}{6}\cdot \frac{1}{6}=\frac{1}{36}\).
Сколько же очков в этом случае должен дать третий бросок? Очевидно, что подойдет 2, 3, 4, 5, 6 – все, кроме 1. Вероятность того, что при третьем броске выпадет число очков, не равное единице, равна \(\displaystyle \frac{5}{6}\).
Значит, вероятность того, что при первых двух бросках выпали единицы, а при третьем – не единица, равна \(\displaystyle \frac{5}{216}\).
Нам подойдет также случай, когда сумма очков за первые 2 броска равна 3. Это значит, что выпали 2 и 1 или 1 и 2, то есть 2 благоприятных исхода из 36 возможных. Вероятность этого события равна \(\displaystyle \frac{2}{36}=\frac{1}{18}\).
При этом нам все равно, что выпадет при третьем броске: очевидно, что сумма очков при трех бросках будет больше трех.
Окончательно получаем: \(\displaystyle \frac{5}{216}+\frac{1}{18}=\frac{17}{216}\approx 0,08\).
Ответ: 0,08
16. Анна Малкова. С какой вероятностью в случайно выбранном месяце високосного года будет 5 воскресений? Ответ округлите до сотых.
Решение:
Если в месяце 31 день, таких месяцев 7, в 28 днях = 4 недели будет 4 понедельника. Остается 3 дня. Вероятность того, что один из них воскресенье, равна \(\displaystyle \frac{3}{7}\).
Если в месяце 30 дней, таких месяцев 4, аналогично, 5 воскресенье с вероятностью \(\displaystyle \frac{2}{7}\).
Если 29 дней, февраль, вероятность 5 воскресений равна \(\displaystyle \frac{1}{7}\).
Получим:
\(\displaystyle \frac{7}{12}\cdot \frac{3}{7}+\frac{4}{12}\cdot \frac{2}{7}+\frac{1}{12}\cdot \frac{1}{7}=\frac{30}{84}=\frac{5}{14}\approx 0,36\).
Ответ: 0,36
17. И. В. Ященко. На одной полке стоит 36 блюдец: 14 синих и 22 красных. На другой полке стоит 36 чашек: 27 синих и 9 красных. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Решение:
Это безумно громоздкая задача из сборников под редакцией И. В. Ященко. На ЕГЭ она (к счастью) не встречается.
Блюдца: 14 синих и 22 красных, всего 36.
Чашки: 27 синих и 9 красных, всего 36.
Обозначим буквой С – синие, К – красные.
По условию, нужно составить 2 чайные пары одного цвета.
Запишем в таблицу подходящие
| Блюдца | СС | КК | КС или СК |
| Чашки | СС | КК | КС или СК |
Вероятность взять 2 синих блюдца: \(\displaystyle \frac{14}{36}\cdot \frac{13}{35}.\)
Вероятность взять 2 синих чашки: \(\displaystyle \frac{27}{36}\cdot \frac{26}{35}.\)
Вероятность взять 2 синих блюдца и 2 синие чашки: \(\displaystyle \frac{14}{36}\cdot \frac{13}{35} \cdot \frac{27}{36}\cdot \frac{26}{35}.\)
Аналогично, вероятность взять 2 красных блюдца и 2 красные чашки: \(\displaystyle \frac{22}{36}\cdot \frac{21}{35} \cdot \frac{9}{36}\cdot \frac{8}{35}.\)
Вероятность взять красное и синее (или синее и красное) блюдце: \(\displaystyle \frac{14}{36}\cdot \frac{22}{35} \cdot 2\) (почему умножаем на 2 – объяснили в теме «Сумма и произведение вероятностей»).
Вероятность взять красную и синюю (или синюю и красную) чашки равна \(\displaystyle \frac{9}{36}\cdot \frac{27}{35} \cdot 2.\)
Вероятность взять красное и синее блюдца и красную и синюю чашки равна \(\displaystyle \frac{14}{36}\cdot \frac{22}{35} \cdot 2\cdot \frac{9}{36}\cdot \frac{27}{35} \cdot 2.\)
Вероятность составить 2 чайных пары одного цвета равна
\(\displaystyle \frac{14}{36}\cdot \frac{13}{35} \cdot \frac{27}{36}\cdot \frac{26}{35}+\frac{22}{36}\cdot \frac{21}{35} \frac{9}{36}\cdot \frac{8}{35}+\frac{14}{36}\cdot \frac{22}{35} \cdot 2 \frac{9}{36}\cdot \frac{27}{35} \cdot 2=\)
\(=\displaystyle \frac{1}{36^2\cdot35^2}\cdot(14\cdot13\cdot27\cdot36+22\cdot21\cdot9\cdot8+14\cdot22\cdot9\cdot27\cdot4)=\)
\(=\displaystyle \frac{1}{35^2\cdot36\cdot4}\cdot(14\cdot13\cdot3\cdot26+22\cdot21\cdot8+14\cdot22\cdot27\cdot4)=\)
\(=\displaystyle \frac{1}{5\cdot35\cdot36\cdot4}\cdot(2\cdot13\cdot3\cdot26+22\cdot3\cdot8+2\cdot22\cdot27\cdot4)=\)
\(=\displaystyle \frac{1}{5\cdot35\cdot36}\cdot(13\cdot13\cdot3+22\cdot3\cdot2+2\cdot22\cdot27)=\)
\(=\displaystyle \frac{1}{5\cdot35\cdot12}\cdot(13\cdot13+22\cdot2+2\cdot22\cdot9)=\displaystyle \frac{609}{5\cdot35\cdot12}=0,29.\)
Ответ: 0,29
18. В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды.
Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трех играх победила команда А. Какова вероятность того, что эта команда выиграет следующий раунд?
Решение:
Пусть силы команд равны 1, 2, 3, 4, 5 и 6.
В трех раундах участвуют 4 команды, то есть выбирается 4 числа из 6 и среди этих четырех находится наибольшее.
Выпишем в порядке возрастания, какие 4 команды могли участвовать в первых трех раундах:
1234, 1235, 1236, 1245, 1246, 1256, 1345, 1346, 1356, 1456, 2345, 2346, 2356, 2456, 3456 - всего 15 вариантов.
Среди этих 15 групп есть только одна, в которой 4 - наибольшее число. Это группа 1234. Однако, если команда 4 победила команды 1, 2 и 3, то у нее нет шансов выиграть в следующем раунде у команды 5 или 6.
Есть также 4 группы, в которых 5 - наибольшее число. Вероятность того, что команда 5 победила в трех первых раундах, равна \(\displaystyle \frac{4}{15}\). В следующем туре команда 5 встретится либо с командой 6 (и проиграет), либо с командой 1, 2, 3 или 4 и выиграет, то есть в четвертном раунде команда 5 побеждает с вероятностью \(\displaystyle \frac{1}{2}\).
Есть также 10 групп, где 6 - наибольшее число. Вероятность того, что команда 6 победила в трех первых раундах, равна \(\displaystyle \frac{10}{15}\). В четвертом туре команда 6 побеждает с вероятностью 1 (она самая сильная). Соответственно, в следующем туре команда 6 побеждает с вероятностью 1.
Получается \(\displaystyle \frac{4}{15}\cdot\frac{1}{2}+\frac{10}{15}\cdot1=\frac{12}{15}=\frac{4}{5}\) - вероятность команды, победившей в 3 первых турах, победить в четвертном.
Ответ: 0,8.
19. В викторине участвуют 15 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых 8 играх победила команда А. Какова вероятность того, что эта команда выиграет девятый раунд?
Решение в общем виде: (Инна Фельдман)
Команда А победила в 8 играх, следовательно, она сыграла 8 матчей с 8 командами и оказалась самой сильной из них. В этих матчах приняло участие 9 команд.
Рассмотрим команды, которые уже сыграли. Присвоим каждой команде номер в зависимости от ее силы. Самая сильная команда имеет больший номер. Пусть, например, в нашем случае у команды А будет номер 9, а у проигравших команд будут номера от 1 до 8. Вероятность того, что команда А выиграет у всех остальных команд равна вероятности того, что из 9 различных чисел у команды А номер 9. Эта вероятность равна \(\displaystyle \frac{1}{9}\).
Теперь нам нужно найти вероятность того, что команда А выиграет девятый раунд. В девятом раунде добавится еще одна команда. То есть мы будем иметь уже 10 команд, участвующих в викторине. Теперь у нас уже есть как бы набор из 10 различных чисел, характеризующих силу каждой команды. Найдем вероятность противоположного события: "команда А проиграет девятый раунд". Это значит, что десятая команда окажется сильнее, чем команда А. Это произойдет в том случае если из 10 различных неравных чисел у числа, характеризующего силу десятой команды, будет самое большое значение. Вероятность этого события равна \(\displaystyle \frac{1}{10}\).
Отсюда вероятность того, что команда А выиграет девятый раунд равна \(1-\displaystyle \frac{1}{10}=0,9\).
Ответ: 0,9.
В общем случае получаем, что если команда выиграла в \(n\) раундах, то вероятность выиграть в \(n+1\)-м равна \(1-\displaystyle \frac{1}{n+2}\).
Задачи повышенной сложности
20. Однажды агенты Матрицы поймали Морфеуса и дали ему выбирать его же таблетки — красные или синие. Красная возвращает Морфеуса в реальный мир, а синяя навсегда оставляет его внутри Матрицы и в руках агентов. Выбор происходит так: Морфеус сам берёт 50 красных и 50 синих таблеток, как угодно раскладывает их по двум одинаковым коробкам, а потом агент Матрицы сам выбирает любую коробку и не глядя достаёт оттуда случайную таблетку.
Как Морфеусу нужно разложить все таблетки по коробкам, чтобы максимально увеличить свои шансы на возвращение в реальность?
Решение:
Если сложить все таблетки в одну коробку, то шанс вытянуть красную будет \(\displaystyle \frac{50}{100}\) или 50%. Такая же вероятность будет, если разложить синие и красные таблетки по коробкам максимально равномерно: \(\displaystyle \frac{25}{50}\) в каждой коробке. Наша задача — увеличить эту вероятность.
Чтобы это сделать, Морфеус должен в одну коробку положить только одну красную таблетку, а в другую коробку — все остальные таблетки вместе. Теперь посчитаем новые вероятности.
Шанс, что агент выберет коробку, где лежит только одна таблетка, — 50%, потому что коробки одинаковые. А шанс вытянуть красную таблетку, когда в коробке и так только одна красная, — 100%.
Шанс, что агент выберет вторую коробку, равен 0,5. В ней 49 из 99 таблеток красные. В этом случае шанс на спасение равен \(0,5\cdot\displaystyle \frac{49}{99}\approx 0,5\cdot0,495\) примерно 0,2475.
Общая вероятность 74,75%.
Получается, что Морфеусу удалось повысить свои шансы на спасение почти в полтора раза!
Ответ: Общая вероятность 74,75%. Морфеус должен в одну коробку положить только одну красную таблетку, а в другую коробку — все остальные таблетки вместе.
21. Теплоход приходит к пристани между 12.00 и 13.00.
Автобус отходит от пристани между 12.25 и 12.40. Пассажиру требуется 10 минут, чтобы перейти от теплохода к остановке автобуса. Найти вероятность того, что он успеет на автобус.
Решение:
Классическая задача о встрече.
Пассажир может оказаться на остановке автобуса между 12.10 и 13.10.
Если пассажир пришел на остановку автобуса не позднее 12.25, то он успел на автобус с вероятностью 1.
Вероятность прийти на остановку с 12.10 до 12.25 равна \(\displaystyle \frac{1}{4}\) (15 минут из 60 минут).
Если пассажир пришел на остановку позже 12.40, то вероятность успеть на автобус для него равна нулю.
Найдем, с какой вероятностью пассажир успеет на автобус, если придет на остановку между 12.25 и 12.40.
Чтобы успеть, пассажир должен прийти на остановку раньше автобуса.
Отметим на горизонтальной оси \(x\) время прибытия пассажира на остановку.
На вертикальной оси \(y\) – время отхода автобуса.
Чтобы пассажир успел, необходимо условие: \(x\leq y\) (время, когда пассажир появился на остановке, не больше, чем время отъезда автобуса).
Это область над прямой \(y=x\) на нашем рисунке.
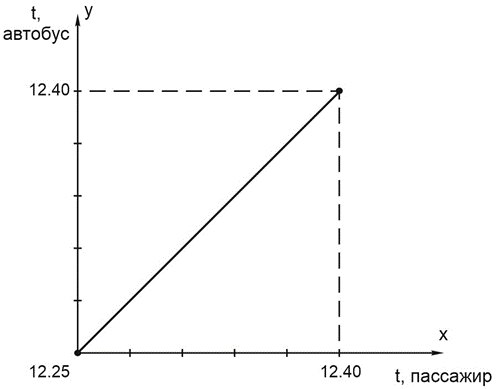
Общему множеству исходов соответствует площадь квадрата на рисунке.
Множеству благоприятных исходов – площадь над прямой \(y=x\), то есть половина площади квадрата.
Если пассажир пришел на остановку между 12.25 и 12.40, вероятность успеть на автобус равна \(\displaystyle \frac{1}{2}\).
А вероятность того, что пассажир придет между 12.25 и 12.40, равна \(15:60=\displaystyle \frac{1}{4}\).
Значит, вероятность успеть на автобус равна \(\displaystyle \frac{1}{2}+\frac{1}{4}\cdot\frac{1}{2}=\frac{3}{8}=0,375.\)
Ответ: 0,375.
22. У одного молодого человека было две подруги, и жили они в противоположных концах города – на востоке и западе, на одной и той же линии метров. Молодой человек работал в центре города. Каждый день после работы он спускался в метро и садился на первый приходящий поезд. В какую сторону поедет поезд — к той девушке он и отправлялся.
Количество поездов в каждую сторону одинаковое, но парень стал замечать, что в какое бы время он ни выходил с работы, к «западной» девушке он приезжал в три раза чаще, чем к той, что жила на востоке. Он подумал, что это судьба, и женился на ней.
Что это – судьба или теория вероятностей? Как такое могло быть?
Если придумаете (или наоборот, никак не получится решить) – напишите нам: online@ege-study.ru
































