Темы для повторения:
Геометрический смысл производной
Графический метод решения задач с параметрами
Друзья, мы продолжаем тему «Задачи с параметрами». Это №18 Профильного ЕГЭ по математике. В этой статье рассказано, как в решении задач с параметрами применяется производная.
Рассмотрим следующую задачу:
1. При каких значениях параметра \(a\) уравнение \(\left|x-2\right|=a{log}_2\left|x-2\right|\) имеет ровно \(2\) решения?
Решение:
Поскольку логарифмы определены для положительных чисел, \(\left|x-2\right| >0\). Это значит, что \(x\ne 2.\)
Сделаем замену: \(\left|x-2\right|=t, \; t>0\).
При \(t>0\) каждому значению \(t\) соответствует два значения \(x.\)
Получим уравнение \(t=a{log}_2t.\)
В левой части уравнения — линейная функция, в правой — логарифмическая. Это функции разных типов. Пытаться справиться с таким уравнение аналитически — бесполезно. Попробуем графический способ.
Если \(a=0\), то \(t=0\) и условие \(t>0\) не выполняется. Рассмотрим по отдельности случаи \(a<0\) и \(a>0.\)
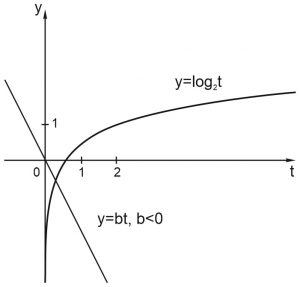
Пусть \(a<0\). Нарисуем графики функций \(y_1=\displaystyle \frac{t}{a}\) и \(y_2={log}_2t.\)
Функция \(y_2={log}_2t\) монотонно возрастает при \(t>0\).
Обозначим \(\displaystyle \frac{1}{a}=b, \; b<0\).
Функция \(y_1=bt\) монотонно убывает при \(t>0.\)
Докажем, что графики функций \(y_1=bt\) и \(y_2={log}_2t\) имеют единственную точку пересечения при \(t>0\) и любом \(b<0\).
Рассмотрим функцию \(z(t)={y_2-y}_1={log}_2t-bt.\)
Функция \(z(t)\) является монотонно возрастающей при \(b<0\) (как сумма монотонно возрастающих функций \({log}_2t\)и
\(-bt\)), следовательно, каждое свое значение, в том числе и значение \(z=0\), она принимает ровно один раз.
Уравнение \({log}_2t-bt=0\) имеет единственное решение при положительных \(t\) и \(b<0\). Значит, при всех \(a<0\) исходное уравнение имеет ровно \(2\) решения. Теперь случай \(a>0\).
\(y_{}={log}_2t. \)
Уравнение \({log}_2t=bt\) имеет единственное решение, если прямая \(y=bt\) касается графика функции \(y_{}={log}_2t.\) Мы помним, как записываются условия касания:
\(\left\{\begin{matrix}
f(x)=kx+b, \\
f'(x)=k.
\end{matrix}\right. \)
В нашем случае
\(\left\{\begin{matrix} log_2t=bt, \\ \displaystyle \frac{1}{tln2}=b.\end{matrix}\right.\)
Учитывая, что \(b=\displaystyle \frac{1}{a}\), получим:
\(\left\{ \begin{array}{c}
\displaystyle \frac{t}{a}={log}_2t, \\
\displaystyle \frac{1}{a}=\frac{1}{tln2}; \end{array}
\Leftrightarrow \left\{ \begin{array}{c}
a=tln2, \\
\displaystyle \frac{1}{ln2}={log}_2t. \end{array}
\right.\right. \)
\({log}_2e={log}_2t,\, \, t=e,\, \, a=eln2. \)
Мы получили, что, \(t=e\) — точка касания. При этом \(a=eln2.\)
Ответ: \(\left[ \begin{array}{c}
a<0, \\
a=eln2.\end{array}
\right.\)
2. При каких \(a\) уравнение \(|x^2-2x-3|-2a=|x-a|-1\) имеет ровно три различных корня?
Решение:
Запишем уравнение в виде: \(|x^2-2x-3|+1=|x-a|+2a.\)
Теперь в левой части уравнения параметра нет. Другими словами, функция \(y=|x^2-2x-3|+1\) в левой части уравнения не зависит от параметра. Ее график неподвижен.
График функции \(y=|x-a|+2a\) получен из графика функции \(y=|x|\) с помощью элементарных преобразований: сдвига на \(a\) по горизонтали и на \(2a\) по вертикали.
Обратите внимание: мы оцениваем, насколько сложно строить графики функций в левой и правой частях уравнения. Стараемся, чтобы более сложная функция не зависела от параметра, то есть чтобы ее график стоял неподвижно. А прямую легче двигать, чем параболу или окружность.
Построим график функции \(y=|x^2-2x-3|+1.\) Вспомним, как это делается.
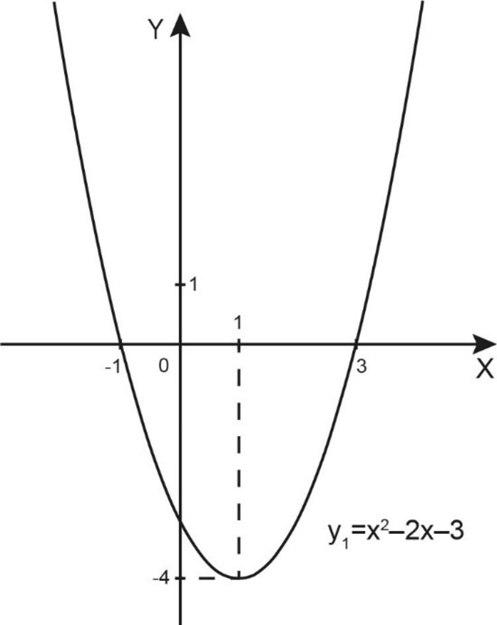
1) Построим график вспомогательной функции \(y_1=x^2-2x-3.\)
Это парабола с ветвями вверх, вершина \((1;-4)\), нули \(-1;3.\)
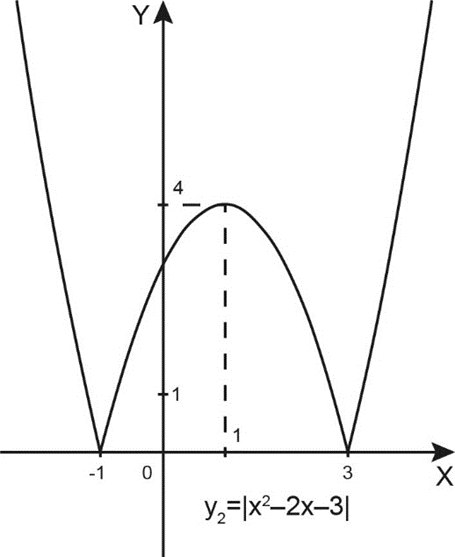
2) Теперь построим график функции \(y_2=|x^2-2x-3|.\)
Те части графика функции \(y_1=x^2-2x-3\), которые располагалась выше оси \(X\), остаются на месте. Часть графика, находившаяся ниже оси \(X\), отражается вверх относительно оси \(X\).
3) Наконец, сдвинув предыдущий график на \(1\) вверх, получим график функции \(f(x)=|x^2-2x-3|+1.\)
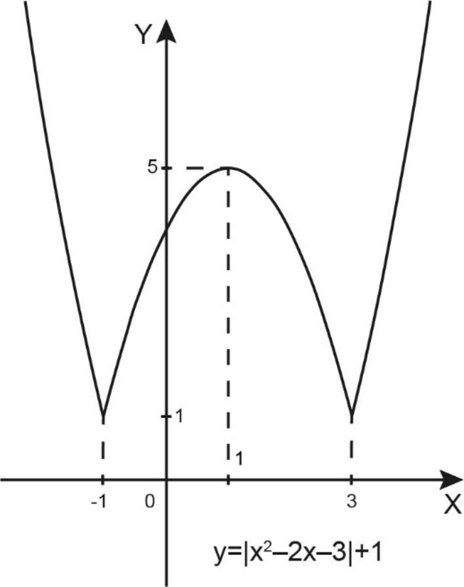
Построим в той же системе координат график функции \(g(x)=|x-a|+2a\). Он получается из графика функции \(y=|x|\) сдвигом на \(a\) по горизонтали и на \(2a\) по вертикали. Другими словами, график функции \(g(x)=|x|\) двигается вдоль прямой \(y=2x\).
Пусть график функции \(g(x)\) проходит через точку \(M (-1; 1)\). При этом \(a=0, \; g(x)=|x|.\)
В этом случае исходное уравнение имеет ровно \(3\) различных корня.
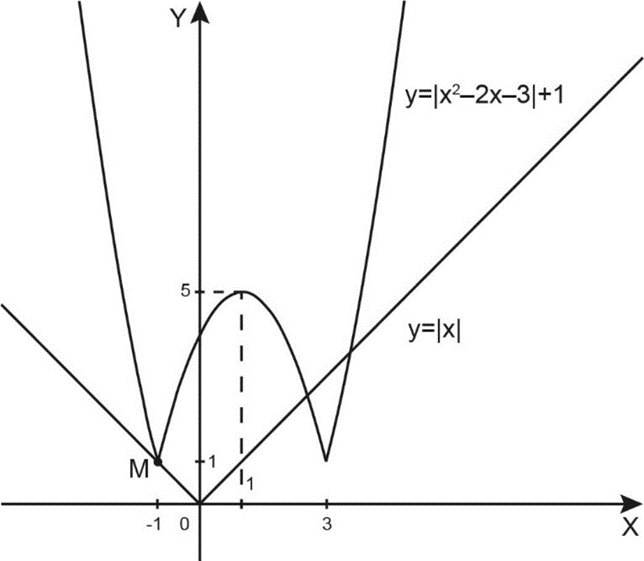
Если график функции \(g(x)\) проходит ниже точки \(M\), корней не больше двух.
Рассмотрим случай, когда график функции \(g(x)\) проходит выше точки \(M\).
На рисунке показаны варианты, когда наше уравнение имеет \(4\) корня и когда имеет \(2\) корня. Но они нам не подходят, мы хотим получить \(3\) корня.
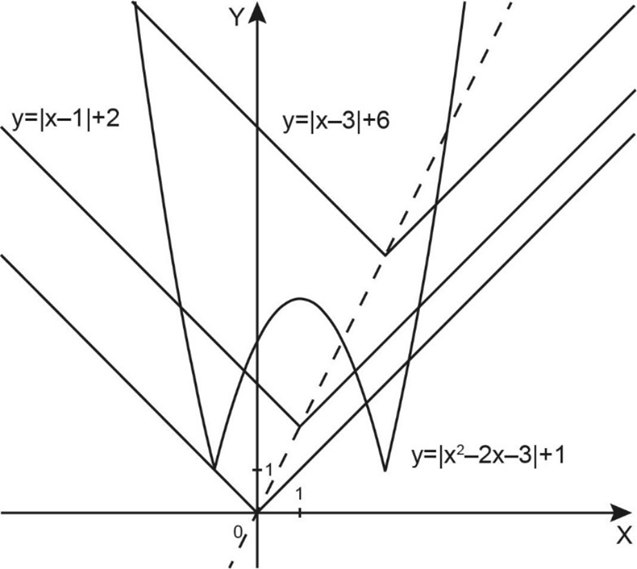
Это произойдет в случае касания графиков функций \(f(x)\) и \(g(x)\) в точке \(A\).
Заметим, что при этом «перевернутый» участок графика функции \(f(x)\) касается левой ветви графика функции \(g(x)\).
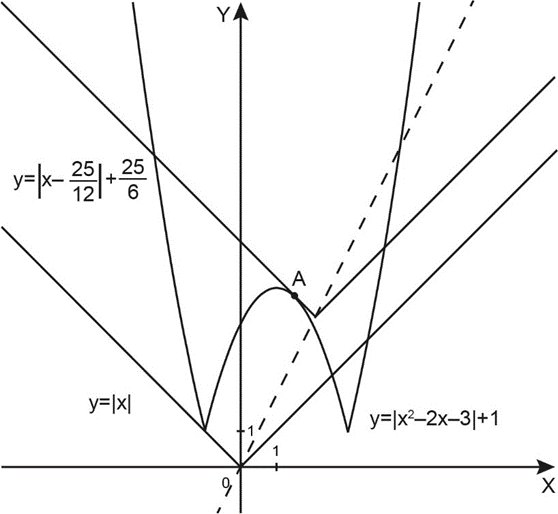
Запишем условия касания для точки \(A\) в общем виде:
\( \left\{\begin{matrix}
f(x)=kx+b, \\
f'(x)=k.\end{matrix}\right.\)
Точка \(A\) лежит на интервале \((-1; 3)\), то есть на «перевернутом» участке графика функции \(f(x)\). На этом участке \(f(x)=-x^2+2x+3+1.\)
В точке \(A\) график функции \(f(x)\) касается левой ветви модуля, то есть для точки \(A\) \(g(x)=3a-x\). Получим:
\( \left\{\begin{matrix}
-x^2+2x+3+1=3a-x, \\
-2x+2=-1.\end{matrix}\right.\)
Решения системы: \(x=\displaystyle \frac{3}{2}\) (абсцисса точки \(A\)), \(a=\displaystyle \frac{25}{12}.\)
Уравнение имеет ровно \(3\) корня, если \(a=0\) или \(a=\displaystyle \frac{25}{12}.\)
Ответ: \(0;\displaystyle \frac{25}{12}.\)