Графический метод решения задач с параметрами

Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.

Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.

Вот список тем, которые стоит повторить:

1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».

2. Преобразование графиков функций.

3. Построение графиков функций.

4. Базовые элементы для решения задач с параметрами.

Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.

Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).

1. При каких значениях параметра a уравнение $\frac{x^2+a^2-4a}{x-a}=0.$ имеет ровно 2 различных решения?

Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.

Получим систему:

$\left\{ \begin{array}{c}x^2+a^2-4a=0 \\x-a\ne 0 \end{array}\right.$

В первом уравнении выделим полный квадрат:

$x^2+a^2-4a+4=4$

$x^2+{(a}^{\ }-2)^2=4$

Это уравнение окружности с центром в точке $P (0; 2)$ и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.

Уравнение $a= x$ задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.

Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.

Кроме того, точка не должна лежать на прямой $a= x$ , которая пересекает окружность в точках $A(0; 0)$ и $B (2; 2).$ Координаты этих точек легко найти, подставим $a= x$ в уравнение окружности.

Точка С также не подходит нам, поскольку при $a = 4$ мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.

Это значит, что $a\in \left(0;2\right)\cup \left(2;4\right).$

2. Найдите все значения a, при которых уравнение $\sqrt{a-2x}=y-x+7$ имеет единственное решение.

Уравнение равносильно системе:

$\left\{ \begin{array}{c}a-2xy={\left(y-x+7\right)}^2 \\y-x+7\ge 0 \end{array}\right.$

Мы возвели обе части уравнения в квадрат при условии, что $y-x+7\ge 0$ (смотри тему «Иррациональные уравнения»).

Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.

$\left\{ \begin{array}{c}a-2xy=y^2+x^2+49+14y-14x-2xy \\y\ge x-7 \end{array}\right.$

Приводим подобные слагаемые в уравнении.

$\left\{ \begin{array}{c}a=y^2+x^2+49+14y-14x \\y\ge x-7 \end{array}\right.$

Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:

$\left\{ \begin{array}{c}a+49={x^2-14x+49+y}^2+14y+49 \\y\ge x-7 \end{array}\right.\Longleftrightarrow \left\{ \begin{array}{c}{\left(x-7\right)}^2+{\left(y+7\right)}^2=a+49 \\y\ge x-7 \end{array}\right.$

Решим систему графически:

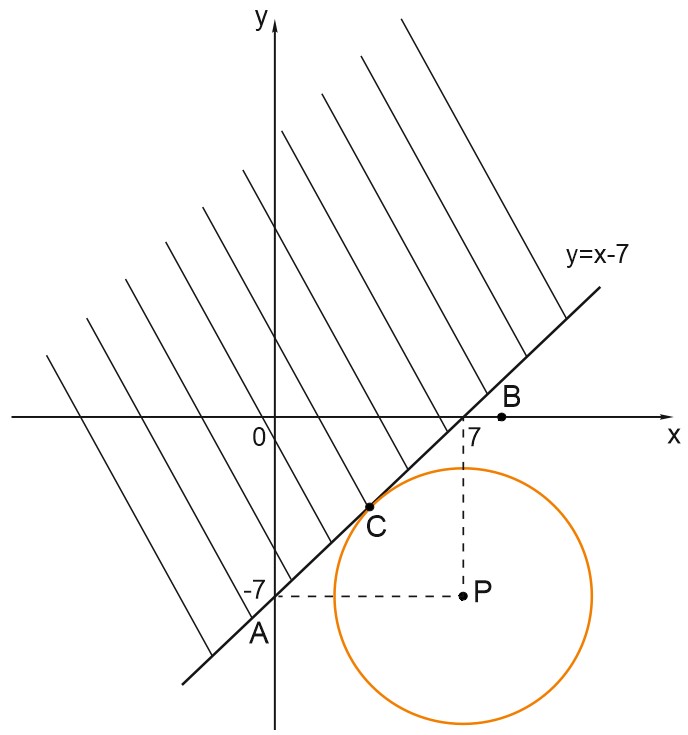
Уравнение ${\left(x-7\right)}^2+{\left(y+7\right)}^2=a+49$ задает окружность с центром в точке $P\ \left(7;\ -7\right)$ , где радиус $R=\sqrt{a+49}.$

Неравенство $y\ge x-7$ задает полуплоскость, которая расположена выше прямой $y=x-7$ , вместе с самой этой прямой.

Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением $y=\ x-7.$

Пусть С — точка касания.

На координатной плоскости отметим точки $A\left(0;-7\right)$ и $B\left(7;0\right)$ , в которых прямая $y=\ x-7$ пересекает оси Y и Х.

Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит $PC=\frac{AB}{2}$ по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.

Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.

$AB=\sqrt{{AP}^2+{BP}^2}$

$AB=\sqrt{7^2+7^2}=\sqrt{98}=7\sqrt{2}.$ Тогда

$\ PC=\frac{AB}{2}$

$\sqrt{a+49}=\frac{7\sqrt{2}}{2};$

Решая это уравнение, получаем, что $a=-24,5.$

Ответ: $a=-24,5.$

3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.

$\left\{ \begin{array}{c}{(\left|x\right|-5)}^2+{(y-4)}^2=4 \\{(x-2)}^2+y^2=a^2\ \ \ \ \ \ \ \ \ \ \ \ \end{array}\right.$

График уравнения ${(x-5)}^2+{(y-4)}^2=4$ - окружность $\omega _1$ с центром $P\ (5;4)$ и радиусом равным 2.

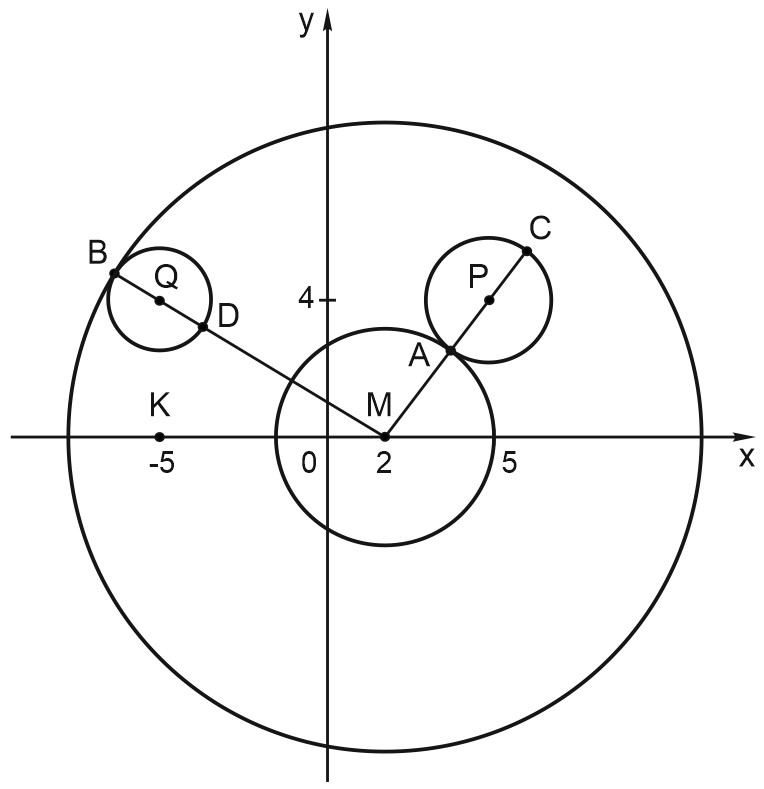
График уравнения ${(\left|x\right|-5)}^2+{(y-4)}^2=4$ - две симметричные окружности $\omega _1$ и $\omega _2$ радиуса 2 c центрами в точках $P\ (5;4)$ и $Q(-5;4)$

Второе уравнение при $a \textgreater 0$ задает окружность $\omega$ с центром в точке $M(2;0)$ и радиусом a.

Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.

Система имеет единственное решение в случаях, когда окружность $\omega$ , задаваемая вторым уравнением, касается только левой окружности $\omega _2$ или только правой $\omega _1 .$

Если a - радиус окружности $\omega$ , то это значит, что $a=MA$ (только правая) или $a=MB$ (только левая).

Пусть А - точка касания окружности $\omega$ и окружности $\omega _1;$

Для точки А:

$MA + AP = MP$ , $MP = 5$ (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4), $MA=\ a=MP-AP=\ 5-2=3.$

В — точка касания окружности $\omega$ и окружности $\omega _2;$

Для точки В:

$MB=MQ+QB;$ длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; $MQ = \sqrt{65}.$ Тогда для точки В получим: $a=MB=\sqrt{65}+2.\$

Есть еще точки С и D, в которых окружность $\omega$ касается окружности $\omega _1$ или окружности $\omega _2$ соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:

$MC=MA+AC=\ 3+4= 7$ , но $\ 7 \textless \sqrt{65}+2$ и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность $\omega _2$ и система будет иметь не одно, а три решения.

Аналогично, для точки D:

$MD=MQ-QD=\sqrt{65}-2\ \textgreater 3,$ и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность $\omega _1$ и система будет иметь три решения.

Ответ: $a=3$ или $a=\sqrt{65}+2.$

4. При каких значениях a система уравнений $\left\{ \begin{array}{c}4\left|y-3\right|=12-3\left|x\right| \\y^2-a^2=3\left(2y-3\right)-x^2 \end{array}\right.\$ имеет 4 решения?

Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)

И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!

$\left\{ \begin{array}{c}3\left|x\right|+4\left|y-3\right|=12 \\x^2+y^2-6y+9=a^2 \end{array}\right.\Longleftrightarrow \left\{ \begin{array}{c}3\left|x\right|+4\left|y-3\right|=12 \\x^2+{\left(y-3\right)}^2=a^2 \end{array}\right.$

Просто выделили полный квадрат во втором уравнении.

Сделаем замену $y-3=t.$ Система примет вид:

$\left\{ \begin{array}{c}3\left|x\right|+4\left|t\right|=12 \\x^2+t^2=a^2 \end{array}\right.$

Вот теперь все видно! Рисовать будем в координатах $(x; t).$

Графиком первого уравнения является ромб, проходящий через точки с координатами $(0; 3); (0; -3); (4; 0)$ и $(-4; 0).$

Графиком второго уравнения является окружность с радиусом $R=\left|a\right|$ и центром в начале координат.

Когда же система имеет ровно 4 решения?

1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.

Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.

Диагонали нашего ромба равны 8 и 6. Значит,

Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

При этом $h=2R.$ Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда $R=\frac{12}{5} = \left|a\right|.$

Мы получили ответ:

$a=\pm \frac{12}{5}$

2) Есть второй случай, и мы его найдем.

Давайте посмотрим — если уменьшить радиус окружности, сделав $R \textless \frac{12}{5}$ , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.

Пусть радиус окружности больше, чем $\frac{12}{5}$ , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.

Пусть радиус окружности равен 3. Тогда система имеет 6 решений.

А что, если $3 \textless R \textless 4$ ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!

Значит, $3 \textless \left|a\right| \textless 4.$ Объединим случаи и запишем ответ:

Ответ: $\left[ \begin{array}{c}\left|a\right|=\frac{12}{5} \\3 \textless \left|a\right| \textless 4 \end{array}\right.$

Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Графический метод решения задач с параметрами» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 08.05.2023

Графический метод решения задач с параметрами

Это полезно