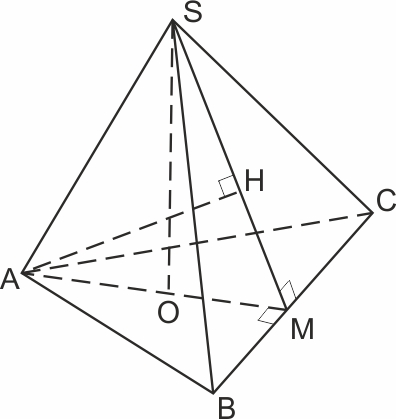
Высота правильной треугольной пирамиды равна 4, а угол между боковой гранью и плоскостью основания равен 60 градусов. Найдите расстояние от вершины основания до плоскости противолежащей ей боковой грани.
Решение:
Обратите внимание на эту задачу. Она содержит базовые схемы для решения очень многих задач по стереометрии.
Прежде всего, определим, где на нашем чертеже угол между плоскостью основания и боковой гранью \(SBC.\) Пусть точка \(M\) — середина \(BC.\)
Проведем \(AM \in (ABC). \ AM\) — медиана и высота правильного треугольника \(ABC\), значит, \(AM \bot BC.\)
Проведем \(SM\in (SBC). \ SM\) — медиана и высота равнобедренного треугольника \(SBC\), значит, \(SM\bot BC.\)
Отсюда следует, что \((ASM)\bot BC\), а угол \( AMS\) — угол между боковой гранью и плоскостью основания, равный \(60^{\circ}\) (по определению угла между плоскостями).
Будем искать расстояние от точки \(A\) до плоскости \((SBC).\)
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.
Нам надо построить прямую, проходящую через точку \(A\) перпендикулярно плоскости \(SBC.\) Вот еще одно определение.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим этой плоскости.
Значит, надо построить отрезок с одним из концов в точке \(A\), перпендикулярный двум пересекающимся прямым в плоскости \((SBC).\)
Проведем \(AH\bot SM\) в плоскости \((ASM).\)
Заметим, что нужно обязательно указывать, в какой плоскости идет построение. Мы не можем провести линию просто в воздухе. Необходима плоскость, в которой лежит эта линия.
Кроме того, \( AH\bot BC,\) так как \(AH \in (ASM), \ (ASM)\bot BC.\)
Получается, что отрезок \(AH\) перпендикулярен двум пересекающимся прямым в плоскости \(SBC\), поэтому \(AH\bot (SBC).\) Значит, \(\left |AH \right | \) — расстояние от \(A\) до плоскости \(SBC.\)
Чтобы найти это расстояние, сделаем плоский чертеж сечения пирамиды плоскостью \(ASM.\)
Пусть точка \(O\) — проекция точки \(S\) на плоскость основания пирамиды. По условию, \(SO=4\) как высота пирамиды.
Из треугольника \(SOM\), где угол \(M\) равен \( 60^\circ\), а угол \(O\) — прямой, найдем \(OM:\)
\(\begin{array}{l} {tg60^{\circ} =\displaystyle \frac{SO}{OM} }; \ {\sqrt{3} =\displaystyle \frac{4}{OM} }; \ {OM=\displaystyle \frac{4}{\sqrt{3} } }. \end{array} \)
Катет, лежащий напротив угла \(OSM\), равного \(30^{\circ}\), равен половине гипотенузы, поэтому \(SM=2OM=\displaystyle \frac{8}{\sqrt{3}} .\)
У правильной пирамиды вершина \(S\) проецируется в центр основания — точку \(O\), которая является центром вписанной и описанной окружностей треугольника \(ABC.\) Также для правильного треугольника \(ABC\) точка \(O\) — точка пересечения его высот, медиан и биссектрис. Значит, по свойству медиан точка \(O\) лежит на \(AM\) и делит \(AM\) в отношении \(2:1\), считая от вершины \(A.\)
Следовательно, \(AM=3OM=\displaystyle \frac{12}{\sqrt{3}} .\)
Воспользуемся методом площадей, записав площадь треугольника \(ABC\) двумя способами.
\(S_{\vartriangle ABC} =\displaystyle \frac{1}{2} AM\cdot SO=\frac{1}{2} SM\cdot AH; \)
\(\displaystyle \frac{12}{\sqrt{3} } \cdot 4=\frac{8}{\sqrt{3} } \cdot AH; \)
\(AH=6. \)
Ответ: 6.
Второй способ решения этой задачи:
Покажем, как решить данную задачу методом объемов. Суть метода — в том, чтобы разными способами записать объем нашей пирамиды, а затем найти неизвестное расстояние от вершины до противоположной грани, которое является высотой пирамиды. Ведь в качестве основания пирамиды мы можем выбрать любую ее грань.
Из прямоугольного треугольника \(SOM\) найдем \(OM =\displaystyle \frac{4}{\sqrt{3}}.\)
Тогда \(SM = \displaystyle \frac{8}{\sqrt{3}}\) и \(AM = \displaystyle \frac{12}{\sqrt{3}}\), так как \(OM = \displaystyle \frac{1}{3} AM\) (по свойству правильного треугольника).
Отсюда \(AB = AC = BC = 8 , \ S_{ABC} = 16{\sqrt{3}}.\) Мы нашли площадь основания пирамиды.
Объем пирамиды \( V = \displaystyle \frac{1}{3} \cdot S_{ABC} \cdot SO = \displaystyle \frac{64}{\sqrt{3}}.\)
С другой стороны, объем пирамиды \(V = \displaystyle \frac{1}{3} \cdot S_{SBC} \cdot AH\), где \(AH\) — неизвестное нам расстояние от вершины \(A\) до плоскости \(SBC\), которое мы и хотим найти.
\( S_{SBC} = \displaystyle \frac{1}{2} \cdot BC \cdot SM = \displaystyle \frac{32}{\sqrt{3}}. \)
Отсюда \(AH = 6. \)