Асимптота – это прямая, к которой график функции подходит бесконечно близко, но не сливается с ней. Чуть позже мы подробно поговорим об этом определении. А для начала покажем на примере, что это такое.
На рисунке изображен график функции \(y=f(x)\).
У этого графика есть интересная особенность: чем больше \(x\), тем ближе подходит график к прямой \(y=3\).
При \(x\to +\infty\) график функции \(y=f(x)\) не пересекает эту прямую, но и не остается параллельным ей.
Если бы мы двигались по графику функции, увеличивая \(x\), мы бы видели, как расстояние до прямой \(y=3\) становится меньше и меньше.
Прямая \(y=3\) – это асимптота для графика функции \(y=f(x)\).
Есть два варианта произнесения этого слова: асимпто́та, или аси́мптота, и оба варианта считаются правильными.
Возможно, это слово для вас пока непривычно. А вот сами асимптоты вы видели много раз.
1. Вспомним, как выглядит знакомый вам с 7-го класса график \(y=\displaystyle \frac{1}{x}.\)
Решение:
Как вы думаете – почему он такой?
Чем больше \(x\), тем меньше \(\displaystyle \frac{1}{x}.\) Если \(x=10,\) то \(y=\displaystyle \frac{1}{10}.\) Если \(x=100,\) то \(y=\displaystyle \frac{1}{100}. \)
Если \(x\) стремится к бесконечности, то \(y\) стремится к нулю.
Сейчас мы все объясним.
Что значит: «\(x\) стремится к бесконечности?» Это значит, что какую бы сколь угодно большую величину мы ни взяли, \(x\) будет больше этой величины. Больше тысячи, больше миллиона и больше \(100\) миллиардов.
Так вот, если \(x\) стремится к бесконечности, то \(y=\displaystyle \frac{1}{x}\) стремится к нулю.
Кратко это записывается так: Если \(x \rightarrow \infty,\) то \(\displaystyle \frac{1}{x} \rightarrow 0.\)
И если \(x\) стремится к бесконечности, то график функции \(y=\displaystyle \frac{1}{x}\) ближе и ближе подходит к оси абсцисс, но не пересекает ее и не сливается с ней.
В этом случае прямая \(y=0\), то есть ось абсцисс, - горизонтальная асимптота для графика функции \(y=\displaystyle \frac{1}{x}\) при \(x\) стремящемся к бесконечности.
А теперь другая ситуация.
Пусть \(x\) стремится к нулю. Это значит, что мы берем значения переменной \(x\) все меньше и меньше. И в какой-то момент увидим, что \(x\) меньше \(\displaystyle \frac{1}{100}\), меньше \(\displaystyle \frac{1}{1000}\dots\)
Какую бы сколь угодно малую величину мы ни взяли, \(x\) будет меньше этой величины.
Кратко это записывается так: \(x \rightarrow 0\). Тогда значение переменной \(y\) стремится к бесконечности, \(\displaystyle \frac{1}{x} \rightarrow \infty.\)
Запишем кратко: Если \(x \rightarrow 0,\) то \(\displaystyle \frac{1}{x} \rightarrow \infty.\)
Это мы и видим на графике.
В самом деле, \(1:\displaystyle\frac{1}{100}=100; \; 1:\frac{1}{1000}=1000\), и чем ближе \(x\) к нулю, тем дальше в бесконечность уходит величина \(\displaystyle \frac{1}{x}.\)
Прямая \(x=0\), или ось ординат, - вертикальная асимптота графика функции \(\displaystyle \frac{1}{x}.\)
2. Еще один пример: функция \(y=\displaystyle \frac{1}{x-2}+3.\)
Решение:
График этой функции получается из графика функции \(y=\displaystyle \frac{1}{x}\) сдвигом на \(2\) единицы вправо и на \(3\) единицы вверх.
Вместе с графиком двигаются и асимптоты.
В этом случае вертикальная асимптота – это прямая \(x=2\), а горизонтальная – прямая \(y=3\).
Обратим внимание, что вертикальная асимптота соответствует значению \(x=2\), при котором знаменатель обращается в ноль.
В точке \(x=2\) функция \(y=\displaystyle \frac{1}{x-2}+3\) не определена. Но всегда ли точка, в которой функция не определена, соответствует вертикальной асимптоте?
3. Рассмотрим функцию \(y=\displaystyle \frac{x^2-9}{x-3}.\) Будет ли у нее вертикальная асимптота \(x=3\)?
Решение:
Чтобы ответить на этот вопрос, разложим выражение в числителе по формуле разности квадратов.
Получим: \(y=\displaystyle \frac{(x-3)(x+3)}{x-3}=x+3\) при \(x \neq 3\).
Никаких вертикальных асимптот здесь нет.
График – прямая \(y=x+3\), причем точка с абсциссой \(3\) на этой прямой – выколотая.
4. Построим эскиз графика функции \(y=\displaystyle \frac{x^2+3x}{x-2}.\)
Решение:
Нули этой функции: \(x=0\) и \(x=-3\).
Запишем формулу функции в виде \(y=\displaystyle \frac{x(x+3)}{x-2}.\)
Точки \(-3; \; 0; \; 2\) разбивают числовую прямую на интервалы, на каждом из которых функция \(y=\displaystyle \frac{x(x+3)}{x-2}\) сохраняет свой знак.
Функция не определена при \(x=2.\) Прямая \(x=2\) – вертикальная асимптота графика этой функции.
Есть ли у функции другие асимптоты? Посмотрим, каким будет ее поведение при \(x \rightarrow \infty.\)
Однако сделать это не так-то просто: с увеличением \(x\) растут и числитель, и знаменатель дроби \(\displaystyle \frac{x^2+3x}{x-2}.\)
Математики говорят, что мы получили неопределенность вида \(\displaystyle \frac{\infty}{\infty}.\) Что делать?
Выделим целую часть в формуле функции: \(\displaystyle \frac{x^2+3x}{x-2}=\frac{x^2-2x+5x}{x-2}=\frac{x(x-2)}{x-2}+\frac{5x}{x-2}=x+\frac{5x}{x-2}.\)
В выражении \(\displaystyle \frac{5x}{x-2}\) разделим и числитель, и знаменатель на \(x\).
Мы можем себе это позволить, поскольку \(x\) стремится к бесконечности и точно не обратится в ноль.
Получим: \(\displaystyle \frac{5x}{x-2}=\frac{5}{1-\frac{2}{x}}.\)
При больших значениях \(x\) величина \(\displaystyle \frac{2}{x}\) стремится к нулю, и мы можем ею пренебречь.
Получим, что чем больше \(x\), тем ближе график функции \(\displaystyle \frac{x^2+3x}{x-2}\) подходит к прямой \(y=x+5\).
Прямая \(y=x+5\) является наклонной асимптотой для графика данной функции.
Вот эскиз графика:
Уравнение наклонной асимптоты, как и всякое уравнение прямой, имеет вид \(y=kx+b\).
В высшей математике существуют специальные формулы для нахождения \(k\) и \(b\) (через пределы).
5. Построим эскиз графика функции \(y=\sqrt{x^2+1}\).
Решение:
Эта функция определена при всех \(x\), так как \(x^2+1>0\) всегда.
Более того, \(x^2+1\geqslant 1\), и значит, область значений функции: \(y \geq1\).
Функция четная, ее график симметричен относительно оси \(Y\).
Поскольку \(x^2+1\geqslant 1\), наименьшее значение функции равно \(1\) и достигается при \(x=0\).
Как же ведет себя эта функция, если \(x \rightarrow \infty\)?
В этом случае \(y=\sqrt{x^2+1}=|x|\cdot\sqrt{1+\displaystyle \frac{1}{x^2}}.\)
Мы вынесли из-под корня \(|x|\), поскольку \(\sqrt{x^2}=|x|.\)
Если \(x \rightarrow \infty ,\) то \(\displaystyle \frac{1}{x^2} \rightarrow 0,\) и график функции \(y=\sqrt{x^2+1}\) ведет себя как \(y=|x|.\)
Это значит, что при \(x \rightarrow +\infty\) наклонной асимптотой будет прямая \(y=x\), а при \(x \rightarrow -\infty\) наклонной асимптотой будет \(y=-x\).
Это наше первое знакомство с асимптотами. Обобщим то, что мы узнали:
Асимптота – такая прямая, к которой график функции подходит бесконечно близко, но не сливается с ней.
Представим себе, что мы движемся по графику функции. Если мы приближаемся к точке, в которой функция не определена, и при этом график функции уходит в бесконечность, приближаясь к некой вертикальной прямой, то эта прямая – вертикальная асимптота.
Если существует такая прямая, что при увеличении \(x\) расстояние от точки на графике функции до этой прямой стремится к нулю, то такая прямая будет горизонтальной или наклонной асимптотой.
Вертикальную асимптоту график функции пересекать не может. А вот горизонтальную или наклонную – может. Такой пример показан на самом первом рисунке в этой главе. Здесь нет противоречия, поскольку о приближении к горизонтальной или наклонной асимптоте имеет смысл говорить, когда значение \(x\) стремится к бесконечности.
Можно сказать, что асимптота кривой – это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность. Расстояние от точки \((x_0; y_0)\) кривой до этой прямой стремится к нулю при движении вдоль ее ветви к бесконечности.
6. Запишите формулы вертикальных и горизонтальных асимптот гипербол:
а) \(y=\displaystyle \frac{3}{x-2}+3;\)
б) \(y=1-\displaystyle \frac{2}{2x+1};\)
в) \(y=\displaystyle \frac{3}{x-2};\)
г) \(y=\displaystyle \frac{10}{x}.\)
Решение:
а) График гиперболы \(y=\displaystyle \frac{3}{x-2}+3\) сдвинут относительно графика \(y=\displaystyle \frac{3}{x}\) на \(2\) вправо и на \(3\) вверх (и растянут в \(3\) раза по вертикали). Значит, вертикальная асимптота \(x=2,\) горизонтальная асимптота \(y=3.\)
б) Преобразуем формулу: \(y=1-\displaystyle \frac{2}{2x+1}=1-\frac{2}{2(x+\frac{1}{2})}=1-\frac{1}{x+\frac{1}{2}}.\)
Вертикальная асимптота \(x=-\displaystyle \frac{1}{2}\), горизонтальная асимптота \(y=1.\)
в) Формула \(y=\displaystyle \frac{3}{x-2}\) задает гиперболу.
Функция определена при \(x \neq 2\), т. е. функция имеет точку разрыва с абсциссой \(2\).
Значит, вертикальная асимптота имеет формулу \(x = 2\).
Так как график функции \(y=\displaystyle \frac{3}{x-2}\) не сдвинут ни вверх, ни вниз, горизонтальная асимптота имеет формулу \(y=0.\)
г) Функция \(y=\displaystyle \frac{10}{x}\) определена при \(x \neq 0\), т. е. функция имеет точку разрыва с абсциссой \(0\).
Значит, вертикальная асимптота \(x=0\), горизонтальная асимптота \(y=0.\)
Ответ: а) \(x=2; \; y=3;\) б) \(x=-\displaystyle \frac{1}{2}; \; y=1;\) в) \(x=2; \; y=0;\) г) \(x=0; \; y=0.\)
7. На каких из рисунков изображены асимптоты графиков функций?
Решение:
Асимптота – это прямая, к которой график функции подходит бесконечно близко, но не сливается с ней.
Вертикальная асимптота соответствует точке, в которой функция не определена. Горизонтальные и наклонные асимптоты – прямые, к которым бесконечно близко подходит график функции, если аргумент стремится к бесконечности.
Асимптоты графиков функции изображены на рисунках 2, 3, 4.
Обратите внимание, что на рисунке 4 график пересекает асимптоту. Но происходит это не в бесконечности, а при некотором \(x<0\). И если \(x \rightarrow \infty\), то график бесконечно близко подходит к асимптоте, но не сливается с ней.
На рисунке 1 график функции приближается к пунктирной прямой на ограниченном участке, но не в бесконечности, поэтому эта прямая не является асимптотой. Значит, асимптоты изображены только на рисунках 2, 3 и 4.
Посмотрим на графики знакомых элементарных функций.
Прямая \(y=0\) – горизонтальная асимптота показательной функции при \(x \rightarrow -\infty\).
График логарифмической функции имеет вертикальную асимптоту \(x=0.\)
График функции \(y=tgx\) имеет бесконечно много асимптот.
Это вертикальные прямые \(x=\displaystyle \frac{\pi}{2}+\pi n,\) где \(n \in Z.\) При таких значениях переменной \(x\) тангенс не определен.
Об элементарных функциях и их графиках читайте здесь.
Посмотрим, как асимптоты помогают строить графики функций.
Подробно о построении графиков функций здесь.
8. Построим график функции \(y=\displaystyle \frac{4x^2}{(x-1)(x+2)}.\)
Решение:
Это дробно-рациональная функция.
Область определения \(D(y): x \neq 1; \; x \neq -2.\)
Нули функции: \(x=0.\)
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: \(x=1; \; x=-2.\)
Если \(x\) стремится к бесконечности, \(y=\displaystyle \frac{4x^2}{(x-1)(x+2)}=\frac{4x^2}{x^2(1-\frac{1}{x})(1+\frac{2}{x})}=\frac{4}{(1-\frac{1}{x})(1+\frac{2}{x})}.\)
Мы сократили числитель и знаменатель в формуле функции на \(x^2\). Мы можем сделать это, поскольку \(x\) стремится к бесконечности и значит, не равен нулю.
Получаем, что чем больше \(x\), тем меньше значения выражений \(\displaystyle \frac{1}{x}\) и \(\displaystyle \frac{2}{x}.\)
Если \(x\) стремится к бесконечности, то этими выражениями можно пренебречь. Тогда \(y\) стремится к \(4\).
Значит, \(y=4\) — горизонтальная асимптота.
Вот эскиз графика:
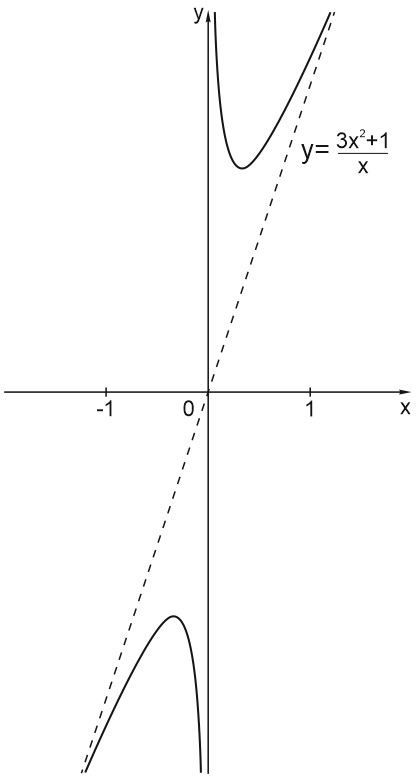
9. Построим график функции \(y=\displaystyle \frac{3x^2+1}{x}.\)
Решение:
В этой задаче нам помогут несколько приемов: выделение целой части, сложение графиков, асимптоты.
Область определения: \(x \neq 0.\)
Выделим целую часть: \(y=\displaystyle \frac{3x^2+1}{x}=3x+\frac{1}{x}.\)
Функция является суммой двух элементарных функций, \(y_1=3x\) и \(y_2=\displaystyle \frac{1}{x}.\)
Если \(x \rightarrow 0\), то \(y \rightarrow \infty\), значит, \(x = 0\) - вертикальная асимптота.
При \(x \rightarrow \infty\) слагаемым \(\displaystyle \frac{1}{x}\) можно пренебречь, и функция ведет себя как \(y=3x.\) Значит, \(y=3x\) – наклонная асимптота. Вот эскиз графика:
10. Построим график функции \(y=\displaystyle \frac{\sin x}{x}.\)
Решение:
Запишем формулу функции в виде \(y=\sin x\cdot \displaystyle \frac{1}{x}.\)
Функция определена при \(x \neq 0.\) Она четная, поскольку является произведением двух нечетных функций \(y=\sin x\) и \(\displaystyle \frac{1}{x}.\) График симметричен относительно оси ординат.
Нули функции – в точках, где \(\sin x =0,\) то есть при \(x =\pi n, \; n \in Z, \; n \neq 0.\) Отметим эти точки на оси \(X\).
Отметим также точки с абсциссой \(x =\displaystyle \frac{\pi}{2}+2\pi n, \; n \in Z.\)
В этих точках значение синуса равно \(1\). Значение функции \(y=\displaystyle \frac{\sin x}{x}\) в этих точках такое же, как и у функции \(\displaystyle \frac{1}{x}.\)
Аналогично для точек, в которых значение синуса равно \(-1\). В них значение функции \(y=\displaystyle \frac{\sin x}{x}\) равно \(\displaystyle -\frac{1}{x}.\)
Если \(x\) стремится к бесконечности, \(y=\displaystyle \frac{\sin x}{x}\) стремится к нулю, то есть при \(x \rightarrow \infty, y \rightarrow 0.\)
Для этой функции ось абсцисс – горизонтальная асимптота, несмотря на то, что график функции пересекает ее бесконечное число раз. График функции подходит ближе и ближе к оси абсцисс, но не сливается с ней.
Соединим полученные точки плавной кривой. График почти готов.
Но что же будет, если \(x\) стремится к нулю? Ведь и \(x\), и \(\sin x\) будут становиться меньше и меньше. Как же будет вести себя частное \(y=\displaystyle \frac{\sin x}{x}\)?
Оказывается, что если \(x\) стремится к нулю, то \(y=\displaystyle \frac{\sin x}{x}\) стремится к единице. В математике это утверждение носит название «Первый замечательный предел».
Интуитивно это можно объяснить так: при малых \(x\) график функции \(y=\sin x\) ведет себя как \(y=x\).
Поэтому, если \(x\) стремится к нулю, то частное \(y=\displaystyle \frac{\sin x}{x}\) стремится к единице.
Конечно, при \(x=0\) наша функция не определена. На графике появится пустая точка.
В итоге получим:
Запишем две полезные формулы для нахождения \(k\) и \(b\) в формуле наклонной асимптоты \(y=kx+b.\)
Эти формулы - для тех, кто знаком с понятием предела функции.
\(k=\displaystyle \lim\limits_{x \to \infty}\frac{f(x)}{x}, b = \lim\limits_{x\to \infty}(f(x)-kx).\)