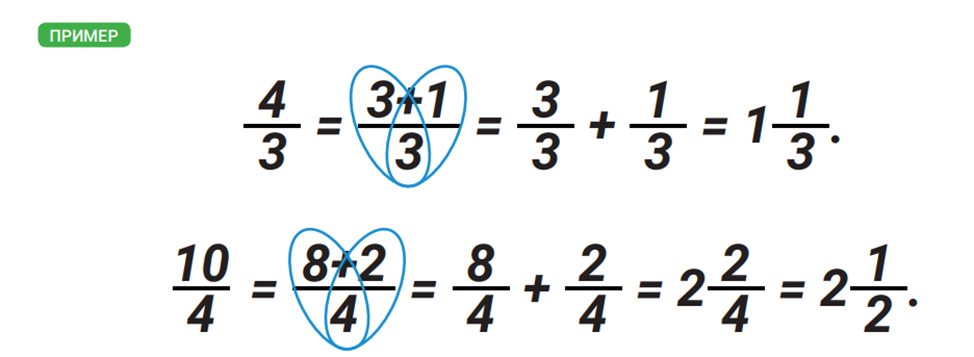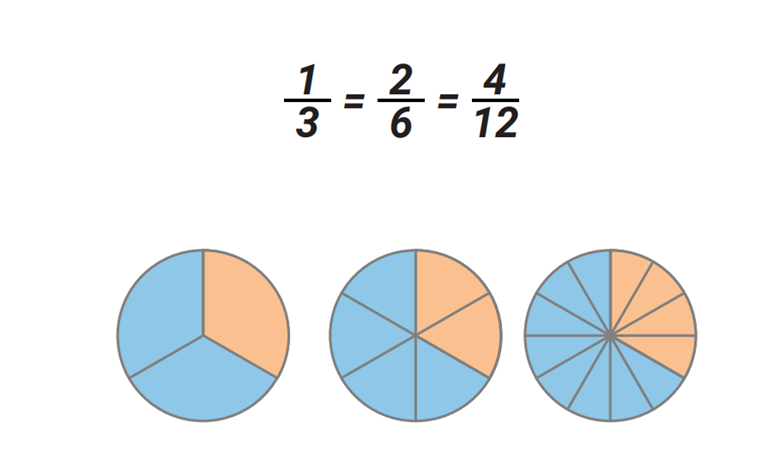Oбыкновенные дроби

Обыкновенные дроби. Действия с дробями. Сложение и вычитание дробей, умножение и деление дробей

Выражение вида \(\frac{a}{b}\) – это обыкновенная дробь.

Число \(a\) над дробной чертой – это числитель, а число \(b\) под дробной чертой – знаменатель.

Правильной обыкновенной дробью называется такая дробь, у которой числитель меньше знаменателя, например,  \(\frac{3}{4}\). А неправильной – когда числитель больше знаменателя: \(\frac{4}{3}\) или \(\frac{9}{7}\).

Если дробь неправильная, ее можно перевести в смешанное число. Такое, где есть и целая, и дробная часть.

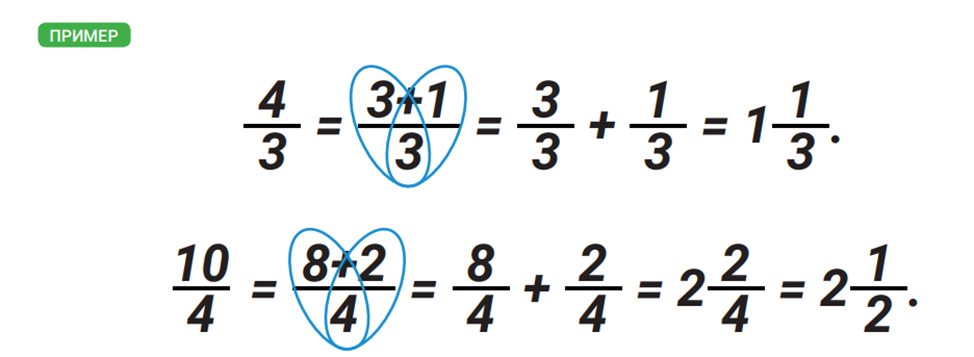
Основное свойство дроби.

Если числитель и знаменатель дроби умножить на одно и то же число, не равное нулю, то получится дробь, равная данной.

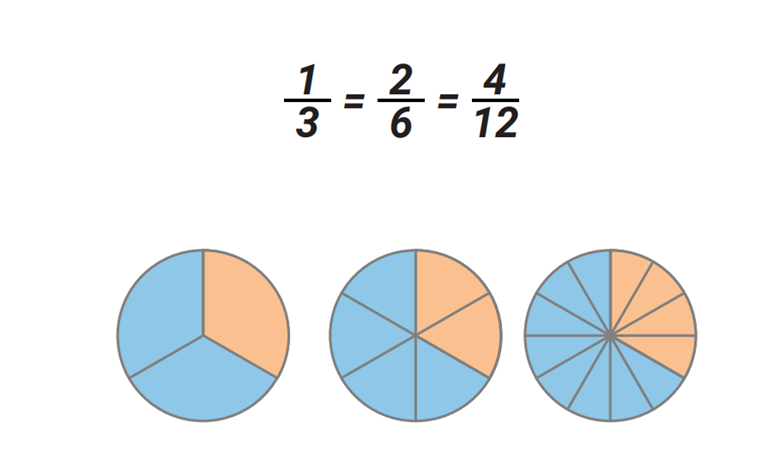
Сокращение дробей

Сократить дробь – значит разложить числитель и знаменатель на множители и вычеркнуть одинаковые множители в числителе и знаменателе.

Действия с дробями

Проще всего складывать дроби с одинаковыми знаменателями.

Мы складываем числители этих дробей, а знаменатель остается прежним.

\(\frac{2}{5}+\frac{1}{5}=\frac{3}{5}\);

\(\frac{6}{7}+\frac{1}{7}=\frac{7}{7}=1\);

\(\frac{5}{8}+\frac{7}{8}=\frac{12}{8}=1 \frac{4}{8}=1 \frac{1}{2}\).

Как быть, если знаменатели разные? В этом случае мы приводим дроби к одинаковому знаменателю. Это то же самое, что и наименьшее общее кратное чисел (кратко НОК).

Наименьшее общее кратное, или НОК, двух и более чисел – это наименьшее натуральное число, которое делится без остатка на каждое из этих чисел. Внимание: оно на них делится.

Например, НОК чисел 15 и 21 равно 105. Вот как мы его нашли:

\(15=3\cdot5\),

\(21=3\cdot7\),

НОК \((15; 21)=3\cdot5\cdot7=105\).

Мы выписали общий множитель чисел 15 и 21, это число 3. И добавили множители 5 и 7, каждый из которых есть только в одном из чисел.

Сложим дроби  \(\frac{2}{3}+\frac{5}{7}\).

НОК \((3;7)=21\), значит, наименьшим общим знаменателем будет число 21. Приведем каждую дробь к этому общему знаменателю. Для этого домножим числитель и знаменатель каждой дроби на дополнительный множитель.

У дроби \(\frac{2}{3}\) знаменатель равен 3, а дополнительный множитель для нее 7 (т.к. \(3\cdot7=21\)). Получим: \( \frac{2\cdot 7}{3\cdot 7}=\frac{14}{21}\). Мы привели первую дробь к знаменателю 21, что нам и нужно для сложения.

Теперь приведем вторую дробь к знаменателю 21.

У дроби \(\frac{5}{7}\) знаменатель равен 7,  дополнительный множитель 3 (потому что \(7\cdot3=21)\),  \(\frac{5\cdot3}{7\cdot3}=\frac{15}{21}\).

Теперь складываем дроби с равными знаменателями.

\(\frac{2}{3}+\frac{5}{7}=\frac{14}{21}+\frac{15}{21}=\frac{29}{21}=1 \frac{8}{21}\).

Выполним вычитание двух дробей с разными знаменателями.

Найдем значение выражения \(\frac{1}{2}-\frac{49}{20}\):

\(\frac{1}{2}-\frac{49}{20}=\frac{10}{20}-\frac{49}{20}=-\frac{39}{20}=-1 \frac{19}{20}=-1 \frac{19\cdot5}{20\cdot5}=-1 \frac{95}{100}=-1,95\).

Сложим три дроби с разными знаменателями. Можно складывать по очереди, либо найти общий знаменатель всех трех дробей и выполнить сложение одновременно:

\(\frac{3}{8}+\frac{1}{6}+\frac{5}{12}=\frac{3\cdot3}{24}+\frac{1\cdot4}{24}+\frac{5\cdot2}{24}=\frac{9+4+10}{24}=\frac{23}{24}\).

Умножить одну обыкновенную дробь на другую очень просто: над дробной чертой будет произведение числителей, а под дробной чертой – произведение знаменателей. Числитель умножаем на числитель, знаменатель умножаем на знаменатель. 

\(\frac{3}{5}\cdot\frac{1}{2}=\frac{3\cdot1}{5\cdot2}=\frac{3}{10}=0,3\).

 
Пример 1.

Перемножим дроби: \(\frac{10}{15}\cdot\frac{9}{2}\).

Решение:

\(\frac{10}{15}\cdot\frac{9}{2}=\frac{2}{3}\cdot\frac{9}{2}=\frac{9}{3}=3\).

Сначала сократили дробь \(\frac{10}{15}\), а затем выполняли умножение. Запомним: если вычисления можно упростить, упрощаем их.

Пример 2.

Найдем значение выражения: \(\Big(\frac{10}{13}+\frac{15}{4}\Big)\cdot \frac{26}{5}.\).

Решение:

\(\Big(\frac{10}{13}+\frac{15}{4}\Big)\cdot \frac{26}{5}=\Big(\frac{40}{52}+\frac{195}{52}\Big)\cdot \frac{26}{5}=\frac{235}{52}\cdot \frac{26}{5}=\frac{47}{2}=23,5.\)

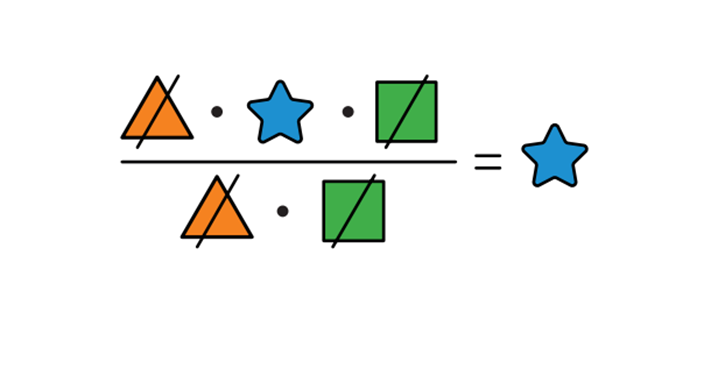
Теперь деление дробей. Как поделить одну дробь на другую?

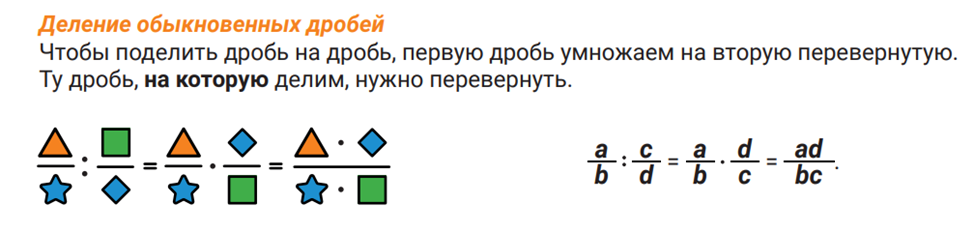
Очень просто – первую дробь умножаем на вторую перевернутую.
Ту дробь, на которую делим, нужно перевернуть.

Пример 3.

\(\frac{12}{5} : \frac{15}{2}=\frac{12}{5}\cdot\frac{2}{15}=\frac{4\cdot2}{5\cdot5}=\frac{8}{25}=0,32\).

Пример 4.

\(\frac{3}{5} : \frac{4}{25}=\frac{3}{5}\cdot\frac{25}{4}=\frac{3\cdot5}{4}=\frac{15}{4}=3 \frac{3}{4}=3,75\).

Пример 5.

Найдите значение выражения: \(\Big(\frac{18}{25}-\frac{9}{11}\Big): \frac{6}{11}.\)

Решение:

Выполним действие в скобках:

\(\frac{18}{25}-\frac{9}{11}=\frac{198}{275}-\frac{225}{275}=-\frac{27}{275}\).

А теперь второе действие – делим обыкновенные дроби

\(-\frac{27}{275}:\frac{6}{11}=-\frac{27}{275}\cdot \frac{11}{6}=-\frac{9}{2}\cdot\frac{1}{25}=-\frac{9}{50}=-0,18\).

Примеры решения задач ОГЭ по теме: Обыкновенные дроби

1. Найдите значение выражения: \(\Big(\frac{19}{8}+\frac{11}{12}\Big): \frac{5}{48}.\)

Решение:

Сначала выполним действие в скобках.

\(\frac{19}{8}+\frac{11}{12}=\frac{19\cdot3}{24}+\frac{11\cdot2}{24}=\frac{57+22}{24}=\frac{79}{24}\).

Сделали действие - проверьте, можно ли сократить дробь. А выделять целую часть пока не надо, потому что следующее действие – деление на дробь.

\(\frac{79}{24}\div\frac{5}{48}=\frac{79}{24}\cdot\frac{48}{5}=\frac{79}{1}\cdot\frac{2}{5}=\frac{158}{5}=31 \frac{3}{5}=31,6\).

2. Найдите значение выражения:

\(\frac{1}{\frac{1}{18}-\frac{1}{21}}.\)

Решение:

Первое действие – найдем разность в знаменателе:

\(\frac{1}{18}-\frac{1}{21}=\frac{7}{126}-\frac{6}{126}=\frac{1}{126}.\)

Трехэтажные дроби стараемся не писать.

\(1: \frac{1}{126}=\frac{1}{1}:\frac{1}{126}=\frac{1}{1}\cdot\frac{126}{1}=126.\)