ЕГЭ-2025 Задача 14 — 1. Решение

В правильной треугольной призме \(ABCA_{1}B_{1}C_{1}\) отметили точки \(M\) и \(K\) на ребрах \(AA_{1}\) и \(A_{1}B_{1}\) соответственно. Известно, что \(AM=5MA_{1}, \; A_{1}K=KB_{1}.\) Через точки \(M\) и \(K\) провели плоскость \(\alpha\) перпендикулярно плоскости \(ABB_{1}.\)

а) Докажите, что плоскость \(\alpha\) проходит через вершину \(C_{1}.\)

б) Найдите площадь сечения призмы \(ABCA_{1}B_{1}C_{1}\) плоскостью \(\alpha\), если все ребра призмы равны 12.

Решение:

а) Построим \(\alpha \perp (AA_{1}B_{1}).\)

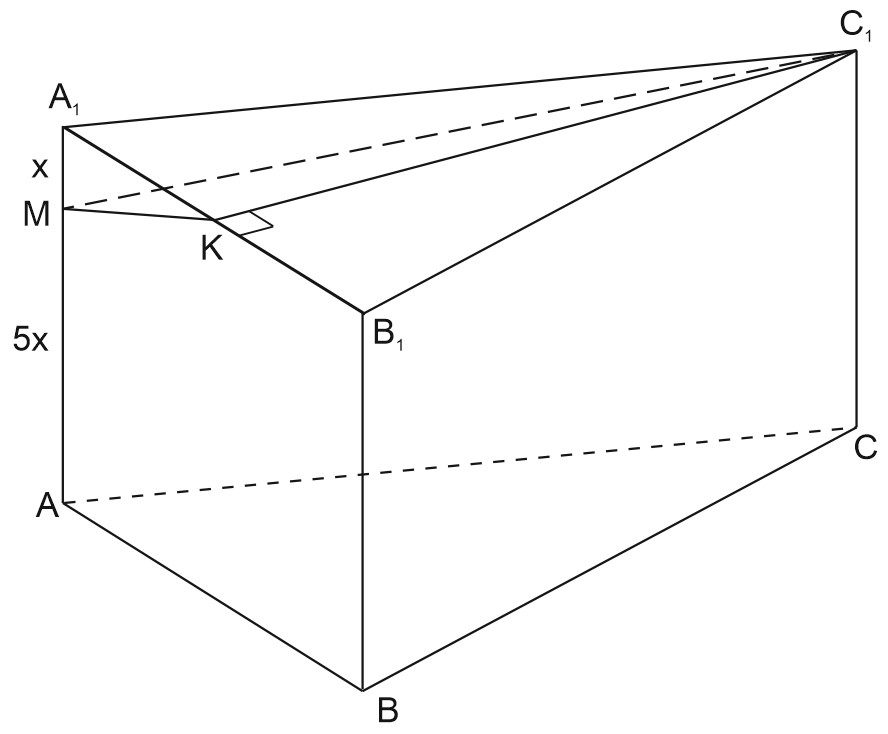
\(\left.\begin{matrix} C_{1}K\perp A_{1}B_{1} \\C_{1}K\perp AA_{1} \end{matrix}\right\}\Rightarrow C_{1}K\perp (ABB_{1})\) по признаку перпендикулярности прямой и плоскости.

Тогда \((MKC_{1})\perp (ABB_{1})\) по признаку перпендикулярности плоскостей.

Из точки \(C_{1}\) можно провести единственный перпендикуляр на прямую \(A_{1}B_{1}.\)

Плоскость построена, \(C_{1}\in \alpha .\)

б) \(C_{1}K\) - высота, медиана и биссектриса правильного треугольника \(A_{1}B_{1}C_{1}.\)

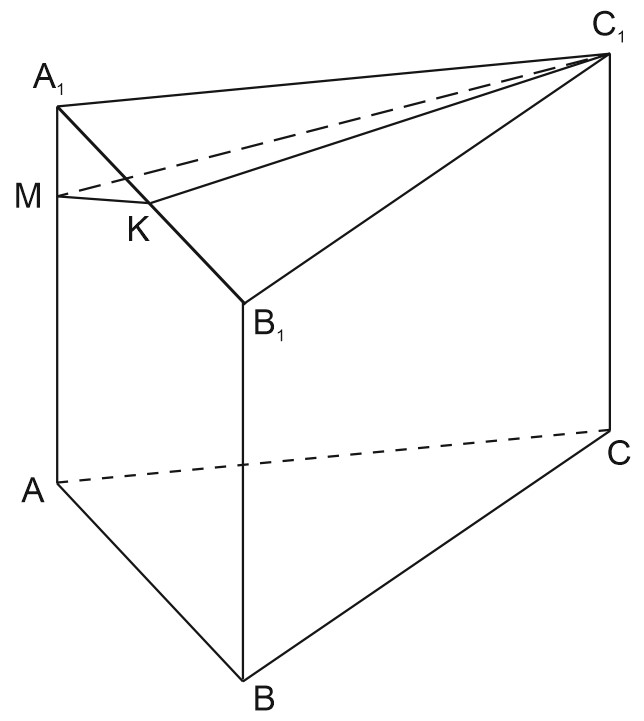
\(C_{1}K=A_{1}B_{1}\cdot \displaystyle \frac{\sqrt{3}}{2}=6\sqrt{3}.\)

\(C_{1}K\perp (ABB_{1})\Rightarrow C_{1}K\perp MK, \; \triangle MKC_{1}\) - прямоугольный.

Также \(\triangle A_{1}MK\) - прямоугольный, \(\angle A_{1}=90^{\circ}.\)

\(A_{1}K=6, \; A_{1}M=\displaystyle \frac{1}{6}AA_{1}=2.\)

По теореме Пифагора, \(MK=\sqrt{A_{1}K^{2}+A_{1}M^{2}}=\sqrt{36+4}=2\sqrt{10}.\)

\(S_{\triangle MKC_{1}}=\displaystyle \frac{1}{2}C_{1}K\cdot MK=\displaystyle \frac{1}{2}\cdot 6\sqrt{3}\cdot 2\sqrt{10}=6\sqrt{30}.\)

Ответ: б) \(6\sqrt{30}.\)