ЕГЭ-2025 Задача 14 — 2. Решение

В правильной четырехугольной пирамиде \(SABCD\) известно, что \(AB=1.\) Через точку \(O\) пересечения диагоналей основания перпендикулярно ребру \(SC\) провели плоскость \(\alpha.\)

а) Докажите, что плоскость \(\alpha\) проходит через вершины \(B\) и \(D.\)

б) В каком отношении плоскость \(\alpha\) делит ребро \(SC\), считая от вершины \(S\), если площадь сечения равна \(\displaystyle\frac{\sqrt{2}}{3}\)?

Решение:

а) Проведем \(BH\perp SC, \; \triangle BCH=\triangle DCH\) по углу и 2 сторонам \(\Rightarrow DH\) - высота \(\triangle DCH, \; DH\perp SC.\)

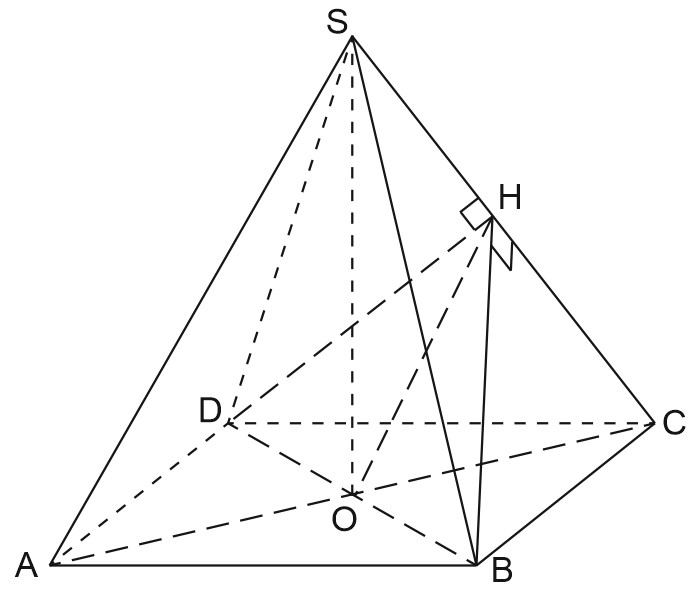
\((BDH)\perp SC\) по признаку перпендикулярности прямой и плоскости.

\(O\in (BDH), \; (BDH)\) совпадает с \(\alpha.\)

б) Найдем \(SH:HC.\)

По условию, \(S_{\triangle BDH}=\displaystyle \frac{1}{2}BD\cdot OH=\displaystyle \frac{\sqrt{2}}{3}.\)

Из \(\triangle ABD: \; BD=\sqrt{AB^{2}+AD^{2}}\) по теореме Пифагора.

\(BD=\sqrt{2},\) тогда \(\displaystyle \frac{1}{2}\cdot \sqrt{2}\cdot OH=\displaystyle \frac{\sqrt{2}}{3}, \; OH=\displaystyle \frac{2}{3}.\)

\(OH\in (BDH) \Rightarrow OH\perp SC.\)

Из \(\triangle OCH\) по теореме Пифагора: \(HC^{2}=\sqrt{OC^{2}-OH^{2}}=\displaystyle \frac{1}{2}-\frac{4}{9}=\frac{1}{18}.\)

\(HC=\displaystyle \frac{\sqrt{2}}{6}.\)

Рассмотрим \(\triangle OSC\) - прямоугольный.

По свойству высоты прямоугольного треугольника, \(OH^{2}=SH\cdot HC \Rightarrow SH=\displaystyle \frac{OH^{2}}{HC}=\frac{4\cdot 6}{9 \cdot \sqrt{2}}=\frac{4\sqrt{2}}{3};\)

\(SH:HC=\displaystyle \frac{4\sqrt{2}}{3}:\frac{\sqrt{2}}{6}=\frac{4\cdot 6}{3}=8:1.\)

Ответ: б) \(8:1.\)