Дана правильная четырехугольная пирамида \(SABCD\) с основанием \(ABCD.\) Плоскость \(\alpha\) проходит через ребро \(AB\) и пересекает ребра \(SC\) и \(SD\) в точках \(M\) и \(N\) соответственно. Известно, что \(AB=AN=BM=5MN.\)
а) Докажите, что \(SM:MC=SN:ND=1:4.\)
б) Найдите косинус угла между плоскостью \(\alpha\) и плоскостью основания пирамиды.
Решение:
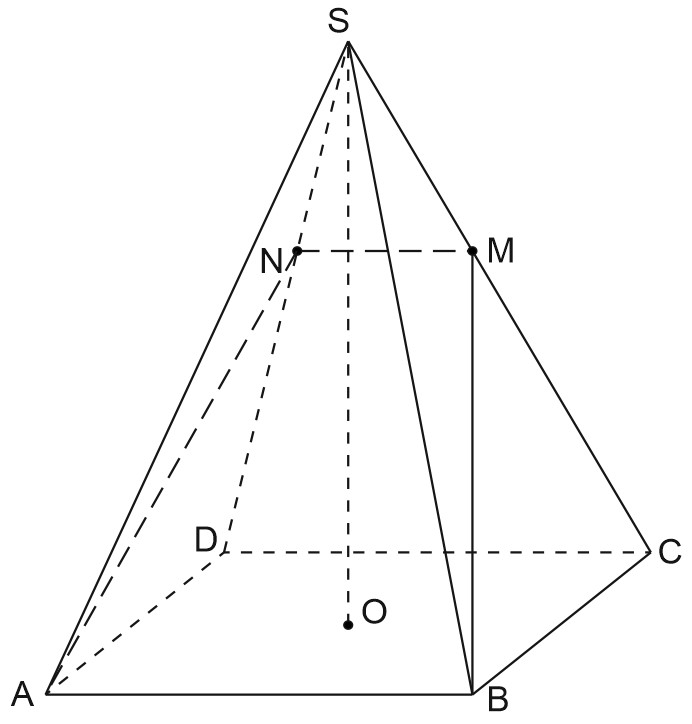
а) Докажем что \(SM:MC=SN:ND=1:4.\)
\(AB\parallel CD\Rightarrow AB\parallel (SCD)\) по принципу параллельности прямой и плоскости.
\(AB\in (ABM); \; (ABM)\cap (SCD)=MN.\)
По теореме о прямой и параллельной ей плоскости, \(MN\parallel AB \Rightarrow MN\parallel CD.\)
\(\triangle SNM \sim \triangle SAB \;\) по 2 сторонам, \(\Rightarrow \displaystyle \frac{SN}{SD}=\frac{SM}{SC},\) тогда \(\displaystyle \frac{SD}{SN}=\frac{SC}{SM};\)
\(\displaystyle \frac{SN+ND}{SN}=\frac{SM+MC}{SM}\Rightarrow 1+\frac{ND}{SN}=1+\frac{MC}{SM};\)
\(\displaystyle \frac{ND}{SN}=\frac{MC}{SM}.\)
\(SM:MC=SN:ND.\)
б) Пусть \(M_{1}\) и \(N_{1}\) - проекция точек \(M\) и \(N\) на плоскость основания.
\(ABM_{1}N_{1}\) - проекция трапеции \(ABMN\) на плоскость \((ABC).\)
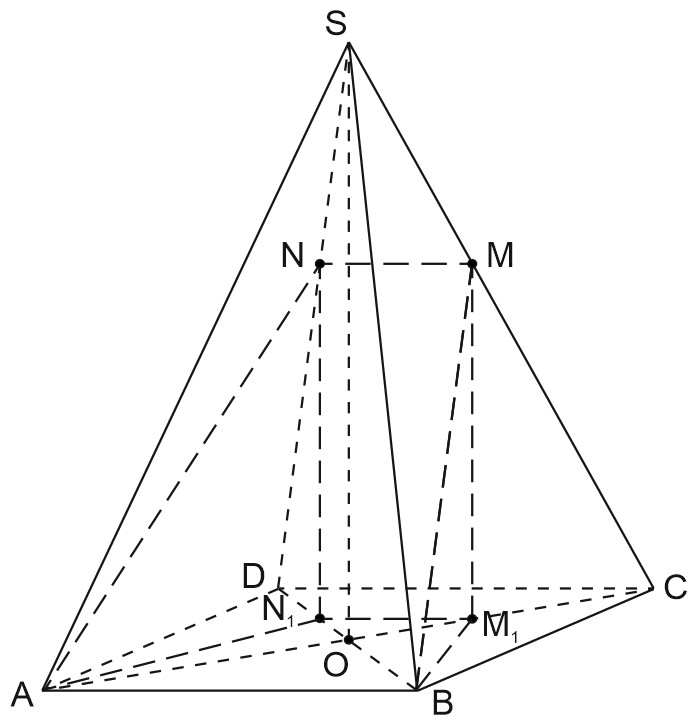
По формуле площади прямоугольной проекции фигуры, \(S_{ABM_{1}N_{1}}=S_{ABMN}\cdot cos\varphi ,\) где \(\varphi \) - угол между плоскостью \((ABM)\) и плоскостью \((ABC).\)
Пусть \(AB=AN=BM=5x, \; MN=x.\)
Проведем \(NH\perp AB, \; MK\perp AB,\) тогда \(AH=BK=2x.\)
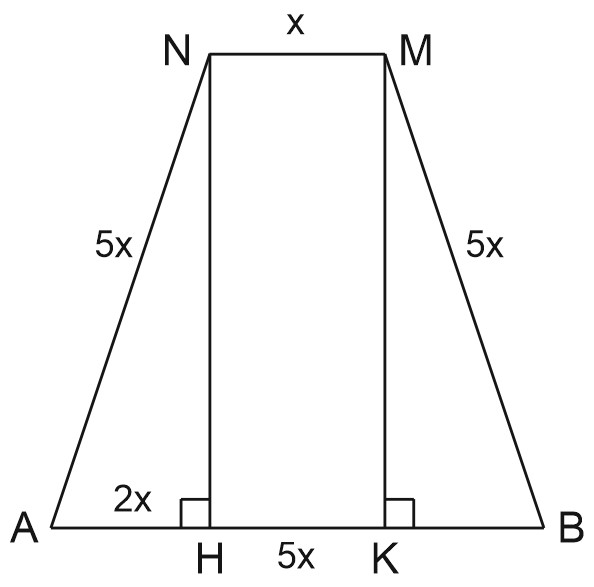
Из \(\triangle ANH: \; NH=\sqrt{AN^{2}-AH^{2}}=\sqrt{21x^{2}}=x\sqrt{21}.\)
\(S_{ABMN}=\displaystyle \frac{1}{2}(AB+MN)\cdot NH=3\sqrt{21}x^{2}.\)
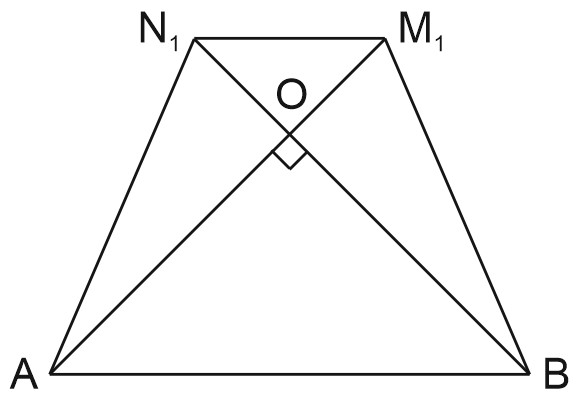
В трапеции \(ABM_{1}N_{1}: \; BN_{1}\perp AM_{1}; \; S_{ABM_{1}N_{1}}=\displaystyle \frac{1}{2}AM_{1}\cdot BN_{1}.\)
\(\triangle SOC \sim \triangle MM_{1}C\) по 2 углам \(\Rightarrow \displaystyle \frac{SM}{SC}=\frac{OM_{1}}{OC}=\frac{1}{5}.\)
\( OM_{1}=\displaystyle \frac{1}{5}OC; \; AM_{1}=BN_{1}=\displaystyle \frac{6}{5}OC.\)
\( OC=\displaystyle \frac{1}{2}\cdot 5x\sqrt{2}, \; AM_{1}=3x\sqrt{2}.\)
\(S_{ABM_{1}N_{1}}=\displaystyle \frac{1}{2}9x^{2}\cdot 2=9x^{2}.\)
\(cos\varphi = \displaystyle \frac{S_{ABM_{1}N_{1}}}{S_{ABMN}}=\displaystyle \frac{9x^{2}}{3\sqrt{21}x^{2}}=\frac{3}{\sqrt{21}}=\frac{\sqrt{21}}{7}.\)
Ответ: б) \(\displaystyle \frac{\sqrt{21}}{7}.\)
В варианте ЕГЭ 2026 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
