Плоскость \(\alpha\) перпендикулярна плоскости основания \(ABCD\) правильной четырехугольной пирамиды \(SABCD\) и пересекает ребро \(SA\) в точке \(K.\) Сечение пирамиды плоскостью \(\alpha\) является правильным треугольником площадью \(2\sqrt{3}.\)
а) Докажите, что плоскость \(\alpha\) перпендикулярна прямой \(AC.\)
б) В каком отношении точка \(K\) делит ребро \(SA\), считая от точки \(S\), если объем пирамиды равен \(36\sqrt{6}.\)
Решение:
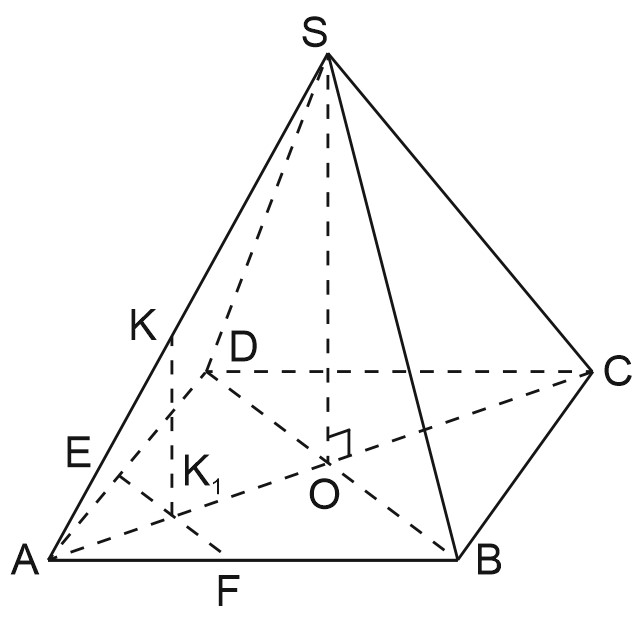
а) Пусть \(SO\) - высота пирамиды. В плоскости \((ASC)\) проведем \(KK_{1}\parallel SO,\) тогда \(KK_{1}\perp (ABC).\)
Пусть \(E\in AD, \; F\in AB, \; K_{1}\in EF.\)
Рассмотрим \(\triangle KEF\) - сечение пирамиды.
По условию, \(\triangle KEF\) - правильный, \(KE=KF,\) тогда \(\triangle KK_{1}E=\triangle KK_{1}F\) по 2 сторонам, \(\Rightarrow K_{1}E=K_{1}F.\)
\(AK_{1}\) - биссектриса \(\angle BAD. \)
\(AK_{1}\) -биссектриса и медиана \(\triangle AEF\Rightarrow \triangle AEF\) - равнобедренный, \(AE=AF.\)
Тогда \(AK_{1}\) - высота \(\triangle AEF, \; AK_{1} \perp AC.\)
Также \(KK_{1}\perp AC \Rightarrow (KEF)\perp AC \) по признаку перпендикулярности прямой и плоскости.
б) \(\triangle KEF\) - правильный. Пусть \(EF=x.\)
\(S_{\triangle KEF}=2\sqrt{3}=\displaystyle \frac{x^{2}\sqrt{3}}{4}\Rightarrow x^{2}=8.\)
\(x=EF=2\sqrt{2}; \; KK_{1}=\displaystyle \frac{x\sqrt{3}}{2}=\sqrt{6}.\)
\(EF\perp AC \Rightarrow EF\parallel BD.\)
\((KEF)\parallel (SBD)\) по признаку параллельности плоскостей, тогда \(KF\parallel SB, \; KE\parallel SD\) (как линии пересечения параллельных плоскостей третьей плоскостью).
\(\triangle AKF \sim \triangle ASB, \; \triangle AK_{1}F \sim \triangle AOB.\)
\(\displaystyle \frac{KF}{SB}=\frac{K_{1}F}{OB}=\frac{EF}{BD}\Rightarrow \triangle SBD\) - правильный.
Пусть \(BD=a,\) тогда \(SO=\displaystyle \frac{a\sqrt{3}}{2}.\)
\(V_{SABCD}=\displaystyle \frac{1}{3}\cdot \frac{a^{2}}{2}\cdot SO=\frac{1}{6}\cdot \frac{a^{3}\sqrt{3}}{2}=\frac{a^{3}\sqrt{3}}{12};\)
\(\displaystyle \frac{a^{3}\sqrt{3}}{12}=36\sqrt{6};\)
\(a^{3}=36\cdot 12\cdot \sqrt{2}=6^{3}\cdot (\sqrt{2})^{3};\)
\(a=6\sqrt{2}=BD.\)
\(\displaystyle \frac{EF}{BD}=\frac{KK_{1}}{SO}=\frac{AK}{SA}\) (из подобия треугольников \(KEF\) и \(SBD, \; AKK_{1}\) и \(ASO\)).
\(\displaystyle \frac{AK}{SA}=\frac{x}{a}=\frac{2\sqrt{2}}{6\sqrt{2}}=\frac{1}{3};\)
\(AK=\displaystyle \frac{1}{3}SA; \; AK:SK=1:2.\)
Ответ: б) \(1:2.\)
В варианте ЕГЭ 2026 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
