ЕГЭ-2025 Задача 14 — 5. Решение

Дана правильная призма \(ABCA_{1}B_{1}C_{1}.\) Точка \(K\) лежит на ребре \(AB\) и делит его в отношении \(AK:KB=3:1.\) Точка \(L\) - середина ребра \(BC.\) Плоскость \(\alpha\) проходит через точки \(K\) и \(L\) и пересекает ребра \(B_{1}C_{1}\) и \(A_{1}B_{1}\) в точках \(M\) и \(N\) соответственно. Известно, что \(B_{1}M:MC_{1}=3:1.\)

а) Докажите что \(MN\perp AB.\)

б) Найдите угол между плоскостью \(\alpha\) и плоскостью основания призмы, если все ребра призмы равны.

Решение:

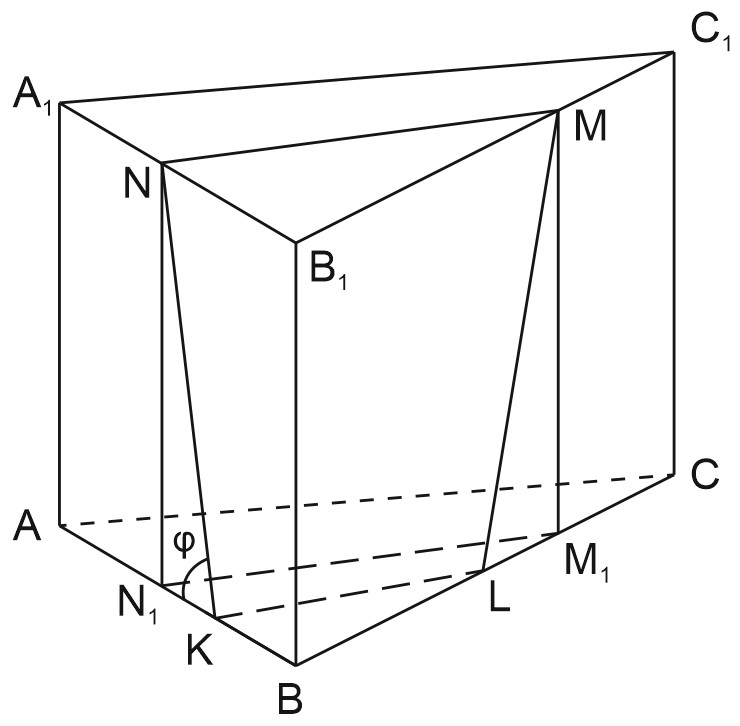
а) \(MN\parallel KL\) как линии пересечения параллельных плоскостей третьей плоскостью.

Пусть \(H\) - середина \(AB, \; CH\) - высота \(\triangle ABC.\)

\(\triangle CBH\sim \triangle LBK\) по 2 сторонам и углу, \(LK\parallel CH, \; CH\perp AB \Rightarrow LK \perp CH.\)

Так как \(MN\parallel LK\Rightarrow MN \perp AB.\)

б) Пусть \(N_{1}\) и \(M_{1}\) - проекция точек \(N\) и \(M\) на плоскость \(ABC.\)

\((MNK) \cap (ABC)=KL, \; N_{1}K\perp KL, \; N_{1}K\) - проекция \(NK\) на \((ABC).\)

По теореме о трех перпендикулярах, \(NK\perp KL.\)

\(\angle NKN_{1}=\varphi \) - угол между \((MNK)\) и \((ABC).\)

Пусть \(AB=BC=AC=AA_{1}=4x.\)

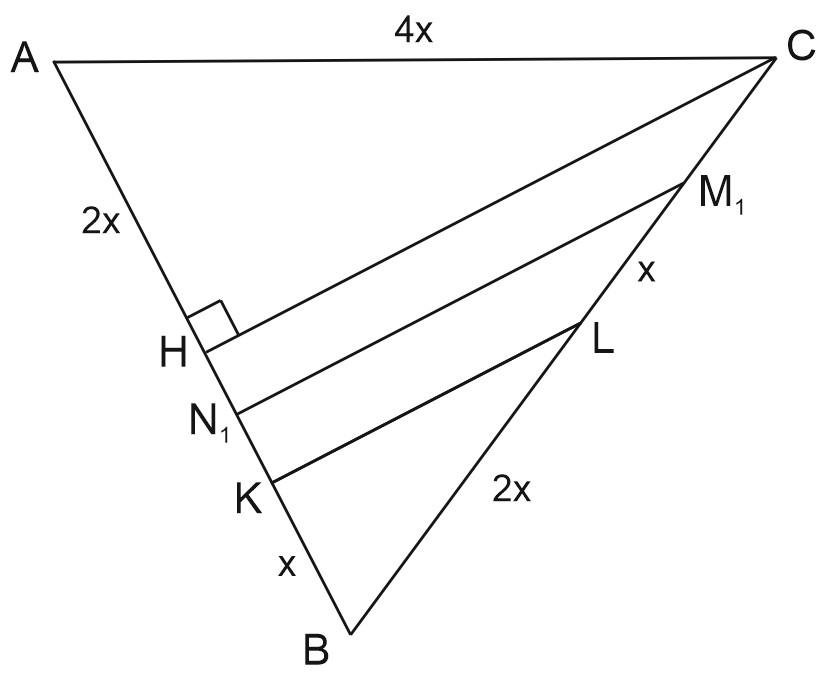
Из \(\triangle NKN_{1}\) найдем \(tg\varphi = \displaystyle \frac{NN_{1}}{N_{1}K}.\)

\(\triangle BN_{1}M_{1}\sim \triangle BKL\) по двум углам, \(\displaystyle \frac{BN_{1}}{BK}=\frac{BM_{1}}{BL}=\frac{3}{2};\)

\(BN_{1}=\displaystyle \frac{3}{2}BK=\frac{3}{2}x,\) тогда \(N_{1}K=\displaystyle \frac{3}{2}x-x=\frac{x}{2}.\)

Из \(\triangle NN_{1}K: \; tg\varphi = \displaystyle \frac{NN_{1}}{N_{1}K}=4x:\frac{x}{2}=8;\)

\(\varphi = arctg8.\)

Ответ: б) \(arctg8.\)