ЕГЭ-2025 Задача 17 — 1. Решение

Дан оcтроугольный треугольник \(ABC.\) Известно, что \(\angle BAC=2\angle ABC.\) Точка \(O\) - центр описанной окружности треугольника \(ABC.\) Вокруг треугольника \(AOC\)описана окружность, которая пересекает сторону \(BC\) в точке \(P.\)

а) Докажите, что треугольники\(ABC\) и \(PAC\) подобны.

б) Найдите \(AB\), если \(BC=6\) и \(AC=4.\)

Решение:

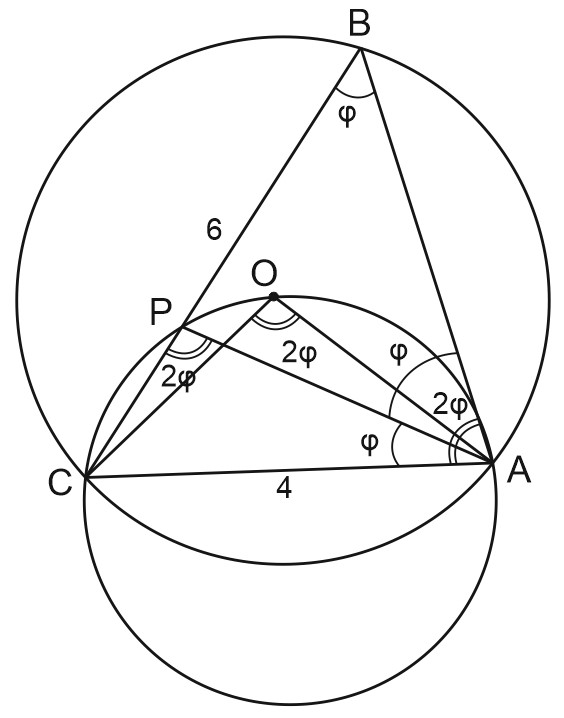
а) Докажем, что \(\triangle ABC\) и \(\triangle PAC\) подобны.

Пусть \(\angle ABC=\varphi.\)

\(\angle ABC\) - вписанный, \(\angle AOC\) - центральный \(\Rightarrow \angle AOC=2\varphi.\)

\(\angle APC=\angle AOC=2\varphi\), так как опираются на общую дугу \(\breve{AC}.\)

\(\triangle APC\sim \triangle BAC\) по двум углам (\(\angle C\) - общий, \(\angle APC=\angle BAC\)), чтд.

б) Найдем \(AB,\) если \(BC=6\) и \(AC=4.\)

Из подобия \(\triangle APC\) и \(\triangle BAC\) следует, что \(\angle PAC=\angle ABC=\varphi.\)

Но \(\angle CAB=2\varphi,\) тогда \(\angle PAB=\varphi\) и \(AP\) - биссектриса \(\angle CAB.\)

По свойству биссектрисы: \(\displaystyle \frac{PC}{PB}=\frac{AC}{AB}.\) (1)

Из подобия \(\triangle APC\sim \triangle BAC\) следует:

\(\displaystyle \frac{AC}{BC}=\frac{CP}{AC}\Rightarrow PC=\frac{AC^{2}}{BC}=\frac{16}{6}=\frac{8}{3},\) подставим в (1).

\(\displaystyle \frac{8}{3}:\Big(6-\frac{8}{3}\Big)=4:AB;\)

\(\displaystyle \frac{8}{3}\cdot \frac{3}{10}=\frac{4}{AB};\)

\(\displaystyle \frac{4}{5}=\frac{4}{AB};\)

\(AB=5.\)

Ответ: б) 5.