ЕГЭ-2025 Задача 17 — 2. Решение

Биссектриса угла \(B\) параллелограмма \(ABCD\) пересекает его сторону \(AD\) в точке \(M\). Диагонали \(AC\) и \(BD\) параллелограмма пересекаются в точке \(O\). Окружность, описанная вокруг треугольника \(ABM\), касается прямых \(BC\) и\(OM.\)

а) Докажите, что \(AB\perp BD.\)

б) Отрезки \(AC\) и \(BM\) пересекаются в точке \(K.\) Найдите площадь четырехугольника \(KODM\), если \(OM=2.\)

Решение:

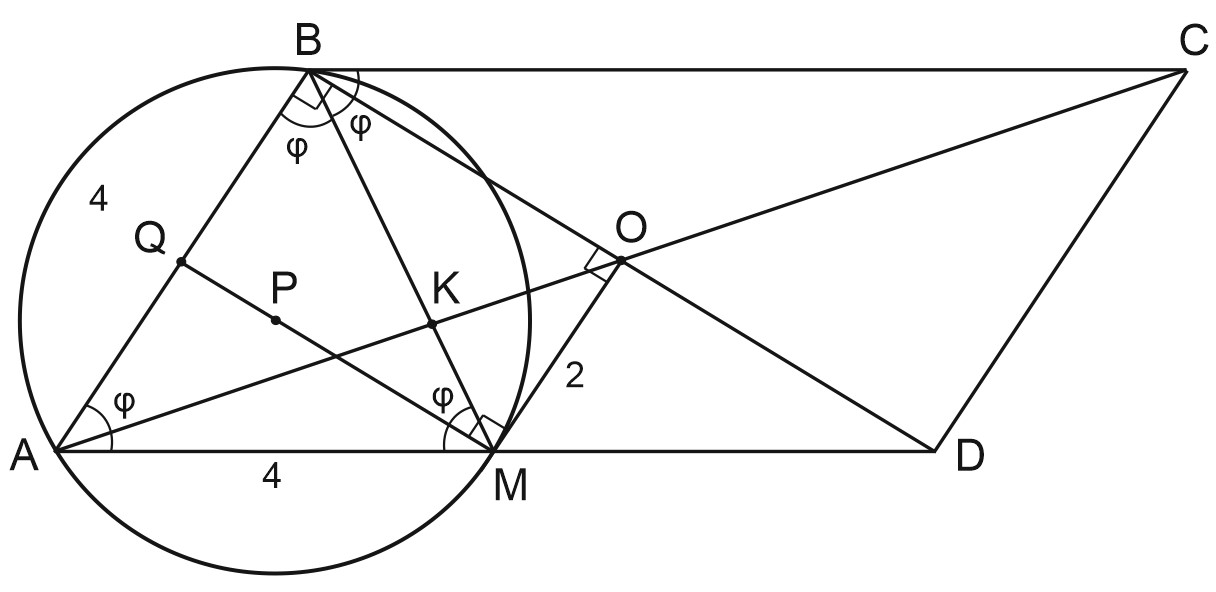
а) Докажем, что \(AB\perp BD.\)

\(BM\) - биссектриса \(\angle ABC\Rightarrow \angle ABM=\angle MBC=\varphi.\)

\(\angle CBM=\angle AMB=\varphi\) (как накрест лежащие углы при параллельных прямых \(BC\) и \(AD\) и секущей \(BM\)).

Тогда \(\triangle ABM\) - равнобедренный.

\(\angle CBM=\varphi\) - угол между касательной и хордой.

\(\angle CBM=\displaystyle \frac{1}{2}\breve{BM}=\angle BAM=\varphi \Rightarrow \triangle ABM\) - правильный.

Пусть \(P\) - центр окружности, описанной около \(\triangle ABM.\)

\(MP\cap AB=Q,\) тогда \(MP\) - медиана, биссектриса и высота \(\triangle ABM.\)

Тогда \(\angle BMQ=30^{\circ}.\)

\(\angle OMQ=90^{\circ}\) (\(OM\) - касательная).

\(MQ\perp AB, \; MQ\perp OM\Rightarrow OM\parallel AB.\)

\(O\) - середина \(BD \Rightarrow OM\) - средняя линия \(\triangle ABD\Rightarrow M\) - середина \(AD,\) значит, \(AM=MD.\)

Но \(AM=BM \Rightarrow BM=MD,\) т. е. \(\triangle BMD\) - равнобедренный, \(O\) - середина \(BD\Rightarrow MO\) - медиана и высота \(\triangle BMD.\)

То есть \(MO\perp BD, \; MO\parallel AB\Rightarrow AB\perp BD.\) чтд.

б) \(AC\cap BM=K.\)

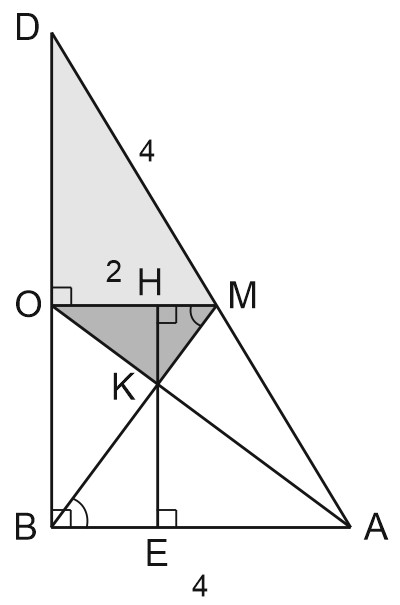
Найдем \(S_{KODM},\) если \(OM=2, \; OM\) - средняя линия \(\triangle ABD\Rightarrow AB=4, \; DM=AB=4.\)

В прямоугольном треугольнике \(ODM\) по теореме Пифагора:

\(OD=\sqrt{DM^{2}-OM^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}.\)

\(S_{\triangle ODM}=\displaystyle \frac{1}{2}OD\cdot OM=\frac{1}{2}\cdot 2\sqrt{3}\cdot 2=2\sqrt{3}.\)

\(OB=OD= 2\sqrt{3}.\)

\(EH\) - высота трапеции \(AMOB, \; EH=OB= 2\sqrt{3}.\)

\(\triangle OKM\sim \triangle AKB\) (по двум углам: \(\angle OKM=\angle AKB\) - вертикальные, \(\angle OMK=\angle KBA\) - накрест лежащие при параллельных прямых \(OM, \; AB\) и секущей \(BM\)).

\(S_{\triangle OMK}=\displaystyle \frac{1}{2}OM\cdot HK;\)

\(\displaystyle \frac{HK}{KE}=\displaystyle \frac{OM}{AB}=\frac{1}{2};\)

\(HK=\displaystyle \frac{1}{3}EH=\frac{2\sqrt{3}}{3}.\)

\(S_{\triangle OMK}=\displaystyle \frac{1}{2}\cdot 2\cdot \frac{2\sqrt{3}}{3}=\frac{2\sqrt{3}}{3}.\)

\(S_{KODM}=S_{\triangle ODM}+S_{\triangle OMK}=2\sqrt{3}+\displaystyle \frac{2\sqrt{3}}{3}=\frac{8\sqrt{3}}{3}.\)

Ответ: б) \(\displaystyle \frac{8\sqrt{3}}{3}.\)