В треугольнике \(ABC\) проведена высота \(AH\) и медиана \(AM\), угол \(ACB\) равен \(30^{\circ}.\) Точка \(H\) лежит на отрезке \(BM.\) В треугольнике \(ACM\) проведена высота \(MQ.\) Прямые \(MQ\) и \(AH\) пересекаются в точке \(F.\) Известно, что \(AM\) - биссектриса угла \(HAC.\)
а) Докажите, что треугольник \(ABC\) прямоугольный.
б) Найдите площадь треугольника \(CFM\) если \(AB=10.\)
Решение:
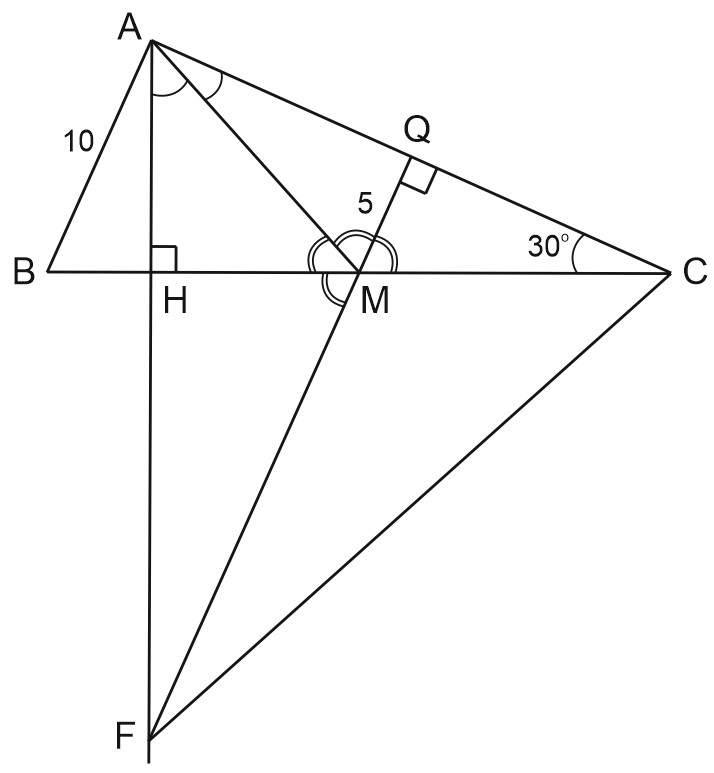
а) Докажем, что \(\triangle ABC\) - прямоугольный.
\(\triangle AHM=\triangle AQM\) по гипотенузе и острому углу \(\Rightarrow \angle AMH=\angle AMQ, \; HM=MQ.\)
\(\angle ACB=30^{\circ}\Rightarrow\) из \(\triangle QMC: \; \angle QMC=60^{\circ},\) значит, смежный \(\angle BMQ=120^{\circ}.\)
Тогда \(\angle AMH=\angle AMQ=60^{\circ}\Rightarrow \angle CAM=30^{\circ}=\angle HAM\Rightarrow \triangle AMC\) - равнобедренный.
\(MQ\perp AC\Rightarrow MQ\) - высота и медиана равнобедренного \(\triangle AMC.\)
То есть \(Q\) - середина \(AC, \; M\) - середина \(BC\Rightarrow MQ\) - средняя линия \(\triangle ABC\Rightarrow MQ \parallel AB\Rightarrow\)
\(\Rightarrow\angle CQM=\angle CAB\) (как соответственные при параллельных прямых \(AB\) и \(MQ\) и секущей \(AC\)).
Тогда \(\angle CAB=90^{\circ},\) то есть \(\triangle ABC\) - прямоугольный.
б) Найдем \(S_{\triangle CFM},\) если \(AB=10.\)
\(AB=10\Rightarrow QM=5\) (как средняя линия).
Из прямоугольного \(\triangle CMQ: \; CM=2QM=10\) (катет против угла в \(30^{\circ}\)).
\(\angle CMF=\angle QMB=120^{\circ}\) (вертикальные); \(HM=MQ=5.\)
\(\angle HMF=\angle QMC=60^{\circ}\) (вертикальные) \(\Rightarrow MFH=30^{\circ}\Rightarrow FM=2HM=10.\)
\(S_{\triangle CFM}=\displaystyle \frac{1}{2}MF\cdot MC\cdot sin\angle CMF=\frac{1}{2}\cdot 10^{2}\cdot sin120^{\circ}=\frac{\sqrt{3}\cdot 100}{2\cdot 2}=25\sqrt{3}.\)
Ответ: \(25\sqrt{3}.\)
В варианте ЕГЭ 2026 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
