В четырехугольник \(KLMN\) вписана окружность с центром \(O.\) Эта окружность касается стороны \(MN\) в точке \(A.\) Известно, что \(\angle MNK=90^{\circ}, \; \angle NKL=\angle KLM=120^{\circ}.\)
а) Докажите, что точка \(A\) лежит на прямой \(LO.\)
б) Найдите длину стороны \(MN,\) если \(LA=1.\)
Решение:
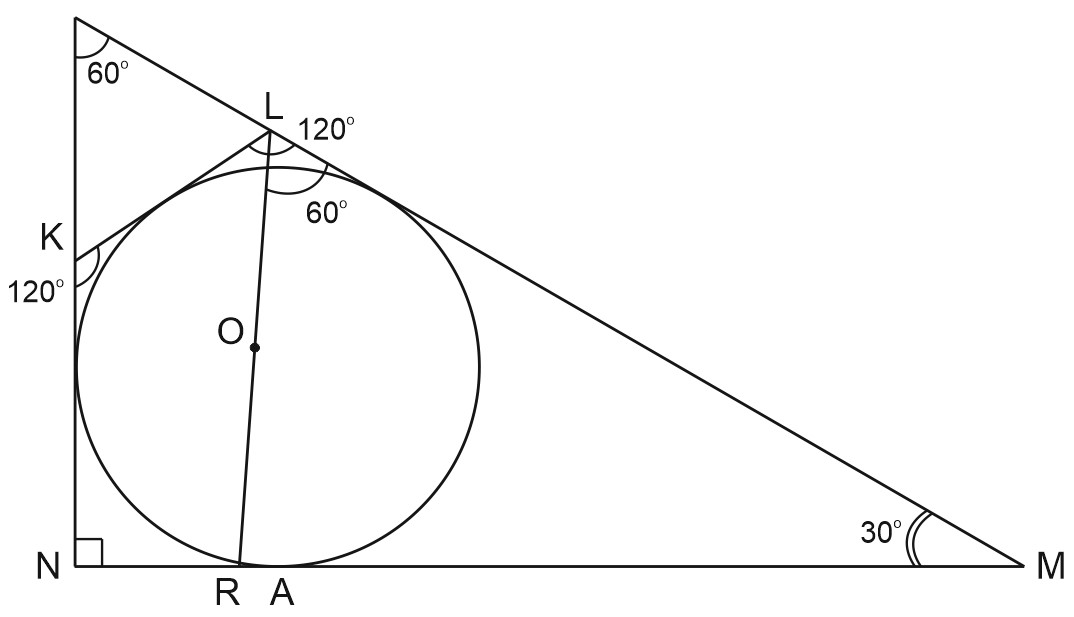
а) Докажем, что \(A\in LO.\)
\(LO\) - биссектриса \(\angle KLM\) (центр окружности, вписанной в угол, лежит на биссектрисе угла).
\(LO\cap MN=R.\) Тогда \(\angle MLR=60^{\circ}.\)
В \(\triangle MLR: \; \angle LRM=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}.\)
Тогда \(OR\perp MN,\) также \(OA\perp MN,\) так как \(OA\) - радиус, \(MN\) - касательная \(\Rightarrow R\) совпадает с \(A\), так как из точки, лежащей на прямой, можно провести единственный перпендикуляр к данной прямой. Значит, \(A\in LO.\)
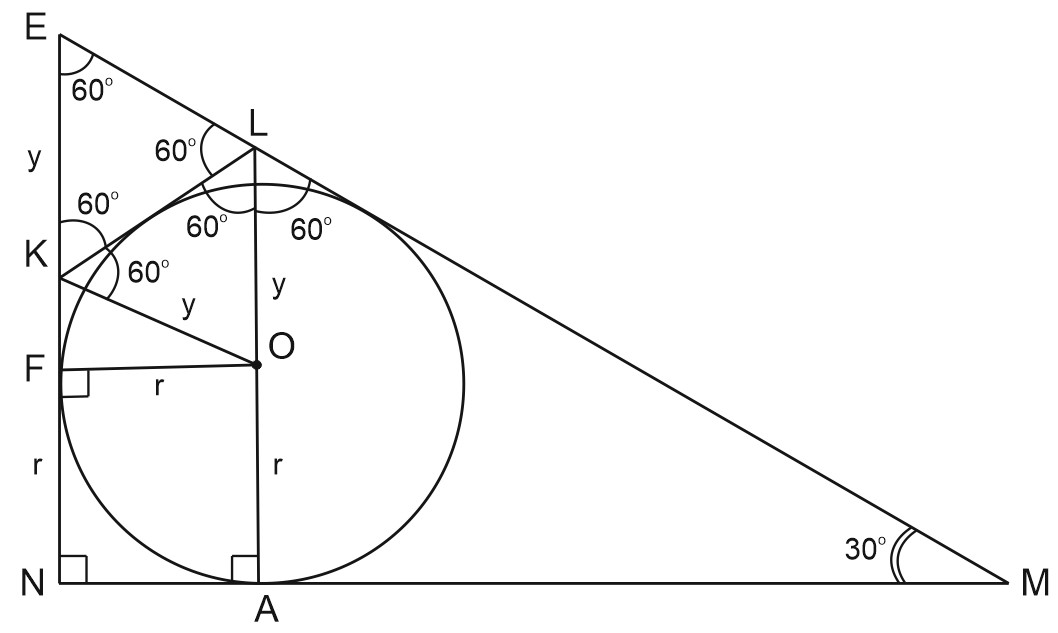
б) Найдем \(MN,\) если \(LA=1.\)
\(NK\cap ML=E; \; \angle EKL=\angle ELK=\angle KEL=60^{\circ} \Rightarrow \triangle EKL\) - правильный.
\(LA=1=OA+OL.\) Пусть \(OA=r, \; OL=y.\)
\(OF\perp NE, \; FOAN\) - квадрат, так как \(\angle A=\angle N=\angle F=90^{\circ}, \; OA=OF=r \Rightarrow FN=r.\)
\(KO\) - биссектриса \(\angle NKL \Rightarrow \angle OKL=60^{\circ}\Rightarrow \triangle OKL\) - правильный, тогда \(KO=EK=OL=y.\)
Тогда \(\angle OKF=60^{\circ}\Rightarrow\) в прямоугольном \(\triangle OKF \angle KOF=30^{\circ}\Rightarrow KF=\displaystyle \frac{y}{2}.\)
\(\displaystyle \frac{r}{y}=sin60^{\circ};\)
\(\displaystyle \frac{r}{y}=\frac{\sqrt{3}}{2};\)
\(y=\displaystyle \frac{2r}{\sqrt{3}}.\)
\(AL=r+y;\)
\(r+\displaystyle \frac{2r}{\sqrt{3}}=1;\)
\((\sqrt{3}+2)r=\sqrt{3}\Rightarrow r=\displaystyle \frac{\sqrt{3}}{\sqrt{3}+2}.\)
Тогда \(ME=r+\displaystyle \frac{y}{2}+y=r+\frac{r}{\sqrt{3}}+\frac{2r}{\sqrt{3}}=\frac{(\sqrt{3}+3)r}{\sqrt{3}}=\frac{\sqrt{3}(1+\sqrt{3})r}{\sqrt{3}}=\)
\(=\displaystyle \frac{(1+\sqrt{3})\sqrt{3}}{(\sqrt{3}+2)}=\frac{3+\sqrt{3}}{\sqrt{3}+2}=\frac{(3+\sqrt{3})(\sqrt{3}-2)}{(\sqrt{3}+2)(\sqrt{3}-2)}=3-\sqrt{3}.\)
Из \(\triangle EMN: \; \displaystyle \frac{NE}{MN}=tg30^{\circ}.\)
\(MN=\sqrt{3}NE=3\sqrt{3}-3.\)
Другой способ: Построим \(OM.\) В прямоугольном треугольнике \(\triangle OMA: \; MA=\displaystyle \frac{r}{tg15^{\circ}}.\)
Ответ: \(3\sqrt{3}-3.\)
В варианте ЕГЭ 2026 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
