ЕГЭ-2025 Задача 18 — 2. Решение

Найдите все значения \(a\), при каждом из которых уравнение

\(a\Big(x+\displaystyle \frac{4}{x}\Big)^{2}+2\Big(x+\displaystyle \frac{4}{x}\Big)-49a+14=0\) имеет ровно два различных корня.

Решение:

Сделаем замену: \(t=x+\displaystyle \frac{4}{x}.\)

Уравнение примет вид: \(at^{2}+2t-(49a-14)=0.\)

Построим эскиз графика функции \(t=f(x)=x+\displaystyle \frac{4}{x}.\)

\(D(f): \; x\neq 0.\) Функция нечетная.

Знаки на интервалах:

• если \(x> 0,\) то \(y> 0;\)
• если \(x< 0,\) то \(y< 0.\)

Нули функции: \(x+\displaystyle \frac{4}{x}=0; \; \frac{x^{2}+4}{x}=0\) - нет решений, не пересекает ось \(Ox.\)

Асимптоты:

• если \(x\to 0,\) то \(t\to \infty , \; x=0\) - вертикальная асимптота;
• если \(x\to \infty ,\) то \(t\sim x , \; t=x\) - наклонная асимптота.

\(f'(x)=\Big(x+\displaystyle \frac{4}{x}\Big)'=1-\displaystyle \frac{4}{x^{2}}=\frac{x^{2}-4}{x^{2}}.\)

\(f'(x)=0\) при \(x=-2\) или \(x=2;\)

\(f(2)=4; \; f(-2)=-4.\)

Знаки производной функции:

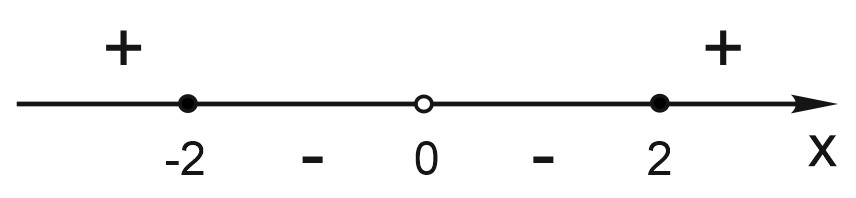
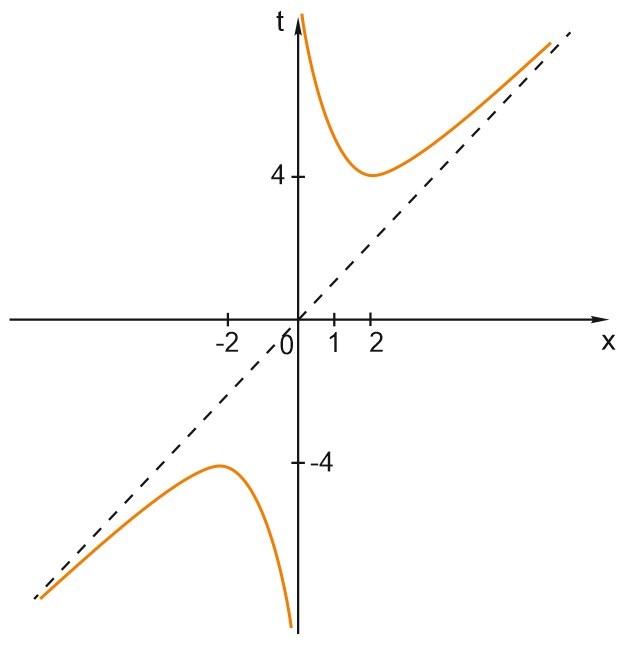
Каждому \(t> 4\) или \(t< -4\) соответствует два значения \(x.\)

\(t=4\) или \(t=-4\) соответствует одно значение \(x.\)

\(-4< t< 4 \; \; \varnothing .\)

Исходное уравнение имеет ровно два различных корня, если уравнение \(at^{2}+2t-(49a-14)=0\) имеет единственное решение.

Это достигается в следующих случаях:

1) \(a=0; \; t> 4\) или \(t< -4;\)

\(2t+14=0;\)

\(t=-7\) - подходит.

2) \(a\neq 0; \; t=4\) или \(t=-4\) - каждому соответствует одно значение \(x.\)

\(at^{2}+2t-(49a-14)=0.\)

Корни \(t_{1}=-4\) и \(t_{2}=4\) не могут быть одновременно, так как по теореме Виета:

\(t_{1}+t_{2}=-\displaystyle \frac{2}{a};\)

\(-4+4=0\neq -\displaystyle \frac{2}{a}.\)

3) \(at^{2}+2t-(49a-14)=0\) - корни \(t_{1}\) и \(t_{2}.\)

\(t_{1}> 4; \; -4< t_{2}< 4\) или \(t_{1}< -4; \; -4< t_{2}< 4.\)

\(D=4+4a(49a-14)=4\cdot 49a^{2}-4\cdot 14a+4=(14a-2)^{2}.\)

\(t_{1}=\displaystyle \frac{-2+(14a-2)}{2a}=7-\frac{2}{a};\)

\(t_{2}=\displaystyle \frac{-2-(14a-2)}{2a}=-7;\)

\(t_{2}=-7< -4,\) тогда \(-4< t_{2}< 4;\)

\(-4< 7-\displaystyle \frac{2}{a}< 4\Leftrightarrow \left\{\begin{matrix} 7-\displaystyle \frac{2}{a}+4> 0, \\7-\displaystyle \frac{2}{a}-4< 0; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \displaystyle \frac{7a-2+4a}{a}> 0, \\\displaystyle \frac{7a-2-4a}{a}< 0; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \displaystyle \frac{11a-2}{a}> 0, \\\displaystyle \frac{3a-2}{a}< 0. \end{matrix}\right.\)

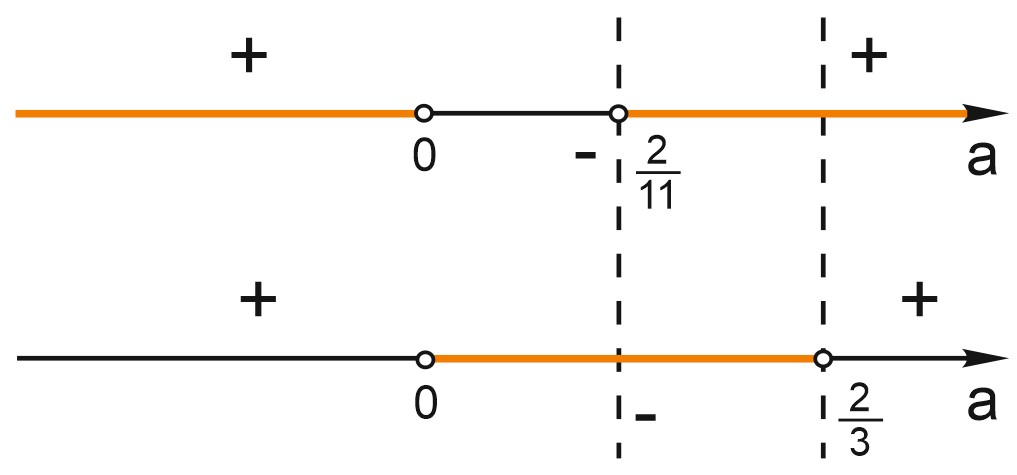
\(a\in \Big(\displaystyle \frac{2}{11};\frac{2}{3}\Big).\)

4) Корни \(7-\displaystyle \frac{2}{a}\) и -7 совпадают:

\(14=\displaystyle \frac{2}{a}; \; a=\frac{1}{7}.\)

При этом \(t=-7< -4\) - подходит.

Ответ: \(a\in \begin{Bmatrix} 0; \displaystyle \frac{1}{7}\end{Bmatrix}\cup \Big(\displaystyle \frac{2}{11};\frac{2}{3}\Big).\)