ЕГЭ-2025 Задача 18 — 4. Решение

Найдите все значения параметра \(a\), при каждом из которых уравнение \((\left | x-a-2\right |+\left | x-a+2\right |)^{2}-a\cdot (\left | x-a-2\right |+\left | x-a+2\right |)+a^{2}-64=0\) имеет ровно два различных корня.

Решение:

Сделаем замену: \(t=\left | x-a-2\right |+\left | x-a+2\right |.\)

Уравнение примет вид: \(t^{2}-at+(a^{2}-64)=0.\)

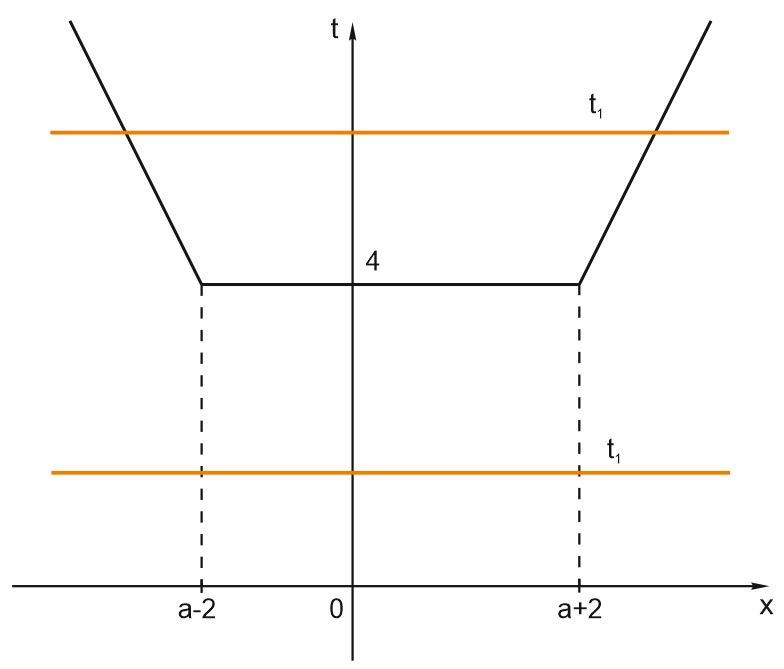
\(t(a-2)=\left | a-2-a-2\right |=4.\)

Исходное уравнение будет иметь два различных корня, если уравнение \(t^{2}-at+(a^{2}-64)=0\) имеет единственное решение.

Это достигается в следующих случаях:

1) Уравнение имеет два корня, таких, что \(\left\{\begin{matrix} t_{1}> 4, \\t_{2}< 4. \end{matrix}\right. (1)\)

2) \(t_{1}=t_{2}> 4.\)

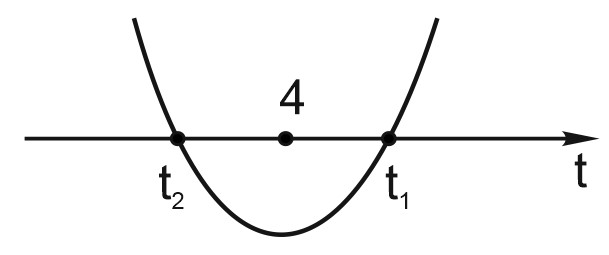
1) Рассмотрим функцию \(f(t)=t^{2}-at+(a^{2}-64)\) - парабола, ветви вверх.

Условия (1) выполняется, если \(f(4)<0.\)

\(16-4a+a^{2}-64<0;\)

\(a^{2}-4a-48<0;\)

\((a-(2-2\sqrt{13}))(a+(2+2\sqrt{13}))< 0.\)

2) \(t_{1}=t_{2}> 4.\)

\(t^{2}-at+(a^{2}-64)=0;\)

\(D=a^{2}-4(a^{2}-64)=-3a^{2}+4\cdot 64=0;\)

\(a=-\displaystyle \frac{16\sqrt{3}}{3}\) или \(a=\displaystyle \frac{16\sqrt{3}}{3}.\)

\(t=\displaystyle \frac{a}{2}.\)

При \(a=-\displaystyle \frac{16\sqrt{3}}{3} \; \; t=-\frac{16\sqrt{3}}{6}<4\) - не подходит.

Сравним \(\displaystyle \frac{16\sqrt{3}}{6}\) и 4.

\(8\sqrt{3}\vee 12;\)

\(2\sqrt{3}\vee 3;\)

\(\sqrt{12}> \sqrt{9}.\)

Следовательно, \(\displaystyle \frac{16\sqrt{3}}{6}> 4.\)

При \(a=\displaystyle \frac{16\sqrt{3}}{3} \; \; t=\frac{16\sqrt{3}}{6}> 4\) - подходит.

Ответ: \((2-2\sqrt{13};2+2\sqrt{13})\cup \begin{Bmatrix} \displaystyle \frac{16\sqrt{3}}{3}\end{Bmatrix}.\)