Часть 1. Задания с кратким ответом
1. Елена Любецкая Петр изготавливает проволочные треугольники со стороной 6,5 см и равными углами. Проволока продается в упаковках по 2 метра. Сколько треугольников получится из 1 упаковки?
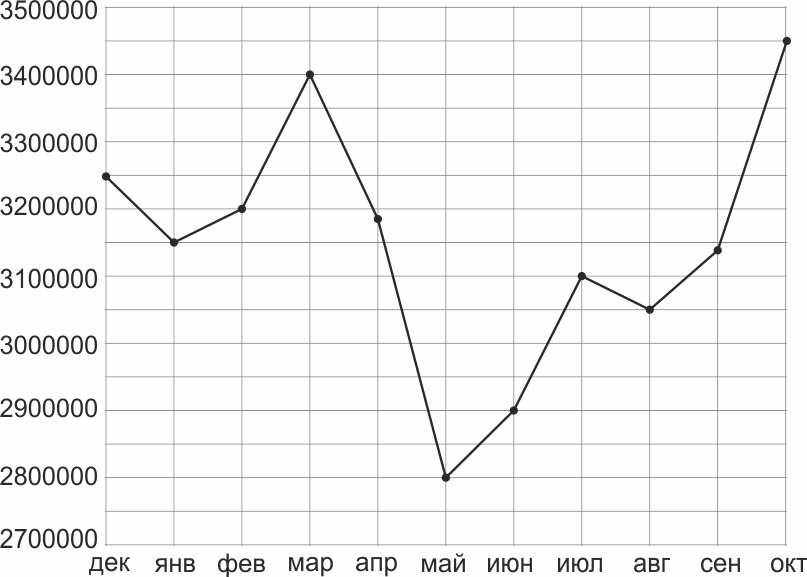
2. На рисунке точками показана аудитория поискового сайта Ya.ru во все месяцы с декабря 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество посетителей сайта хотя бы раз в данном месяце. Для наглядности точки на рисунке соединены линией. Определите по рисунку разность между наибольшей и наименьшей аудиторией сайта Ya.ru в указанный период.
3. Елена Любецкая Пусть \(A (0; 2), B (1; 4), D (2; 0)\). Найдите \(\sqrt{10} \cdot cos BAD\)
4. Елена Любецкая С какой вероятностью синус угла, лежащего в первой четверти, не менее ![]() ?
?
5. Решите уравнение:
\(log_{113} (log_{2} (log_{5} x))=0\)
6. Елена Любецкая В трапеции ABCD ВС и AD – меньшее и большее основания, боковая сторона CD равна 5 и перпендикулярна диагонали АС, диагонали пересекаются в точке О. Найдите АО, зная, что \(tgCOD=2,5\) и \(tgCAD=1,25\).
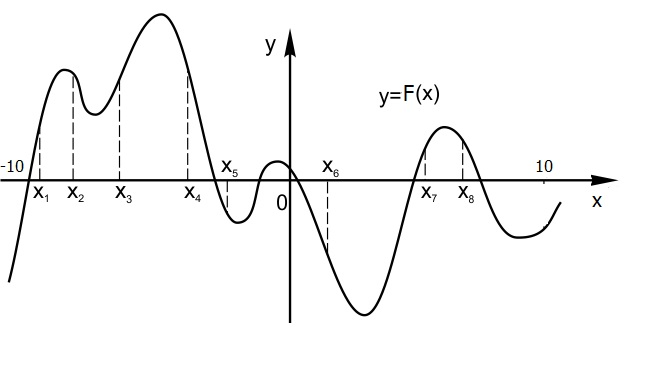
7. На рисунке изображен график \(F(x)\) – первообразной некоторой функции \(f(x)\). На оси абсцисс отмечено 8 точек: \(x_1,x_2, x_3,x_4,x_5, x_6, x_7, x_8\). В скольких из этих точек функция \(f(x)\) принимает положительные значения? В ответ запишите количество точек.
8. Дан куб \(ABCDA_1B_1 C_1 D_1\). Найдите косинус угла \(A_1C_1 D\).
9. Елена Любецкая Вычислите \(tg10^{\circ} \cdot tg20^{\circ} \cdot tg30^{\circ} \cdot \dots \cdot tg80^{\circ}\)
10. Завиcимоcть температуры (в градуcах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экcпериментально и на иccледуемом интервале температур определяетcя выражением \(T(t) = T_0 + bt + at^2\), где t — время в минутах, \(T_0 = 1400 K\), a = −10 К/мин, b = 200 К/мин. Извеcтно, что при температуре нагревателя cвыше 1760 К прибор может иcпортитьcя, поэтому его нужно отключать. Определите, через какое наибольшее время поcле начала работы нужно отключать прибор. Ответ выразите в минутах.
11. От пристани A к пристани B, расстояние между которыми равно 108 км, отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью, на 3 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт B он прибыл одновременно с первым. Ответ дайте в км/ч.
12. Найдите наибольшее значение функции \(y=x^{3}-192x+11\) на отрезке \([-9; 1]\)
Часть 2. Задания с развернутым ответом
13.
а) Решите уравнение \(\left ( \sqrt{2}sin^2 x+ cos x -\sqrt{2} \right )\sqrt{-6 sin x}=0\).
б) Укажите корни этого уравнения, принадлежащие отрезку \([2 \pi ; \frac{7\pi}{2}]\).
14. В пирамиде SABC рёбра AB и SC перпендикулярны. Известно, что \(AC=CS=BS=10\), \(AB=14\); \(BC=8\sqrt{2}\); \(AS=6\sqrt{2}\); точка M принадлежит отрезку AB.
а) Докажите, что площадь сечения CSM минимальна, если плоскость CSM перпендикулярна AB.
б) Найдите объём пирамиды SABC.
15. Решите неравенство: \((3^{\frac{x-2}{2}}-1) \sqrt{3^{x}-10\sqrt{3^{x} }+9} \geq 0.\)
Посмотреть решение Посмотреть ответ
16. Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K.
При этом AK:KC=1:2.
а) Докажите, что \(\angle BAC =30^{\circ}\).
б) Пусть прямые MK и BC пересекаются в точке P, а прямые AP и BK – в точке Q. Найдите KQ, если \(BC=\sqrt{21}\) .
17. В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы:
— каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите x, если известно, что наибольший платёж по кредиту составит не более 1,9 млн рублей, а наименьший — не менее 0,5 млн рублей.
18. Найдите все значения параметра а, при каждом из которых следующая система уравнений имеет хотя бы одно решение (x; y; z)
\(
\left\{\begin{matrix}(x-4sin z)^2+(y+4cos z)^2=1
\\ |x| + |y| =a \hfill
\end{matrix}\right.
\)
19. На доске написано число 2045 и ещё несколько (не менее двух) натуральных чисел, не превосходящих 5000. Все написанные на доске числа различны. Сумма любых двух из написанных чисел делится на какое-нибудь из остальных.
а) Может ли на доске быть написано ровно 1024 числа?
б) Может ли на доске быть написано ровно пять чисел?
в) Какое наименьшее количество чисел может быть написано на доске?
ВНИМАНИЕ преподавателям и владельцам образовательных сайтов. Мы настоятельно просим вас НЕ ВЫКЛАДЫВАТЬ в интернет условия и тем более решения задач. Мы хотим, чтобы участники имели возможность честно решить задачи.