Электрический ток в металлах
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ
Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: носители свободных электрических зарядов в металлах.
В этом листке мы приступаем к подробному изучению того, как осуществляется прохождение электрического тока в различных проводящих средах — твёрдых телах, жидкостях и газах.
Напомним, что необходимым условием возникновения тока является наличие в среде достаточно большого количества свободных зарядов, которые могут начать упорядоченное движение под действием электрического поля. Такие среды как раз и называются проводниками электрического тока.
Наиболее широко распространены металлические проводники. Поэтому начинаем мы с вопросов распространения электрического тока в металлах.
Мы много раз говорили о свободных электронах, которые являются носителями свободных зарядов в металлах. Вам хорошо известно, что электрический ток в металлическом проводнике образуется в результате направленного движения свободных электронов.
к оглавлению ▴
Свободные электроны
Металлы в твёрдом состоянии имеют кристаллическую структуру: расположение атомов в пространстве характеризуется периодической повторяемостью и образует геометрически правильный рисунок, называемый кристаллической решёткой.
Атомы металлов имеют небольшое число валентных электронов, расположенных на внешней электронной оболочке. Эти валентные электроны слабо связаны с ядром, и атом легко может их потерять.
Когда атомы металла занимают места в кристаллической решётке, валентные электроны покидают свои оболочки — они становятся свободными и отправляются «гулять» по всему кристаллу (а именно, свободные электроны перемещаются по внешним орбиталям соседних атомов. Эти орбитали перекрываются друг с другом вследствие близкого расположения атомов в кристаллической решётке, так что свободные электроны оказываются «общей собственностью» всего кристалла). В узлах кристаллической решётки металла остаются положительные ионы, пространство между которыми заполнено «газом» свободных электронов (рис. 1).
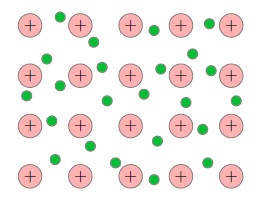
Рис. 1. Свободные электроны
Свободные электроны и впрямь ведут себя подобно частицам газа (другой адекватный образ — электронное море, которое «омывает» кристаллическую решётку) — совершая тепловое движение, они хаотически снуют туда-сюда между ионами кристаллической решётки. Суммарный заряд свободных электронов равен по модулю и противоположен по знаку общему заряду положительных ионов, поэтому металлический проводник в целом оказывается электрически нейтральным.
Газ свободных электронов является «клеем», на котором держится вся кристаллическая структура проводника. Ведь положительные ионы отталкиваются друг от друга, так что кристаллическая решётка, распираемая изнутри мощными кулоновскими силами, могла бы разлететься в разные стороны. Однако в тоже самое время ионы металла притягиваются к обволакивающему их электронному газу и, как ни в чём не бывало, остаются на своих местах, совершая лишь тепловые колебания в узлах кристаллической решётки вблизи положений равновесия.
Что произойдёт, если металлический проводник включить в замкнутую цепь, содержащую источник тока? Свободные электроны продолжают совершать хаотическое тепловое движение, но теперь — под действием возникшего внешнего электрического поля — они вдобавок начнут перемещаться упорядоченно. Это направленное течение электронного газа, накладывающееся на тепловое движение электронов, и есть электрический ток в металле (поэтому свободные электроны называются также электронами проводимости). Скорость упорядоченного движения электронов в металлическом проводнике, как нам уже известно, составляет приблизительно 0,1мм/с.
к оглавлению ▴
Опыт Рикке
Почему мы решили, что ток в металлах создаётся движением именно свободных электронов? Положительные ионы кристаллической решётки также испытывают на себе действие внешнего электрического поля. Может, они тоже перемещаются внутри металлического проводника и участвуют в создании тока?
Упорядоченное движение ионов означало бы постепенный перенос вещества вдоль направления электрического тока. Поэтому надо просто пропускать ток по проводнику на протяжении весьма длительного времени и посмотреть, что в итоге получится. Такого рода эксперимент и был поставлен Э. Рикке в 1901 году.
В электрическую цепь были включены три прижатых друг к другу цилиндра: два медных по краям и один алюминиевый между ними (рис. 2). По этой цепи пропускался электрический ток в течение года.
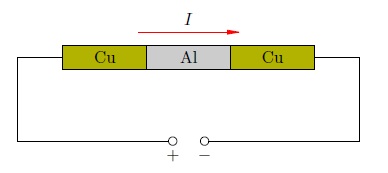
Рис. 2. Опыт Рикке
За год сквозь цилиндры прошёл заряд более трёх миллионов кулон. Предположим, что каждый атом металла теряет по одному валентному электрону, так что заряд иона равен элементарному заряду \(e = 1,6 \cdot 10^{19}\) Кл. Если ток создаётся движением положительных ионов, то нетрудно подсчитать (сделайте это сами!), что такая величина прошедшего по цепи заряда соответствует переносу вдоль цепи около 2кг меди.
Однако после разъединения цилиндров было обнаружено лишь незначительное проникновение металлов друг в друга, обусловленное естественной диффузией их атомов (и не более того). Электрический ток в металлах не сопровождается переносом вещества, поэтому положительные ионы металла не принимают участия в создании тока.
к оглавлению ▴
Опыт Стюарта–Толмена
Прямое экспериментальное доказательство того, что электрический ток в металлах создаётся движением свободных электронов, было дано в опыте Т. Стюарта и Р. Толмена (1916 год).
Эксперименту Стюарта–Толмена предшествовали качественные наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И. Мандельштамом и Н.Д. Папалекси. Они обратили внимание на так называемый электроинерционный эффект: если резко затормозить движущийся проводник, то в нём возникает кратковременный импульс тока. Эффект объясняется тем, что в течение небольшого времени после торможения проводника его свободные заряды продолжают двигаться по инерции.
Однако никаких количественных результатов Мандельштам и Папалекси не получили, и наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит Стюарту и Толмену, которые не только наблюдали указанный электроинерционный эффект, но и произвели необходимые измерения и расчёты.
Установка Стюарта и Толмена показана на рис. 3.
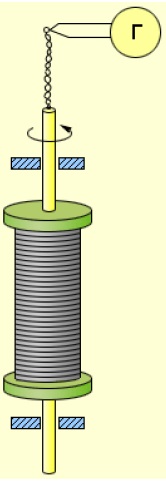
Рис. 3. Опыт Стюарта–Толмена
Катушка большим числом витков металлического провода приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью скользящих контактов были подсоединены к специальному прибору — баллистическому гальванометру, который позволяет измерять проходящий через него заряд.
После резкого торможения катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по цепи, Стюарт и Толмен вычислили отношение \(q/m\) заряда одной частицы к её массе. Оно оказалось равно отношению \(e/m\) для электрона, которое в то время уже было хорошо известно.
Так было окончательно выяснено, что носителями свободных зарядов в металлах являются свободные электроны. Как видите, этот давно и хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что металлические проводники к тому моменту уже более столетия активно использовались в самых разнообразных экcпериментах по электромагнетизму (сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако, заключается в том, что сам электрон был открыт лишь в 1897 году).
к оглавлению ▴
Зависимость сопротивления от температуры
Опыт показывает, что при нагревании металлического проводника его сопротивление увеличивается. Как это объяснить?
Причина проста: с повышением температуры тепловые колебания ионов кристаллической решётки становятся более интенсивными, так что число соударений свободных электронов с ионами возрастает. Чем активнее тепловое движение решётки, тем труднее электронам пробираться сквозь промежутки между ионами (Представьте себе вращающуюся проходную дверь. В каком случае труднее проскочить через неё: когда она вращается медленно или быстро? :-)). Скорость упорядоченного движения электронов уменьшается, поэтому уменьшается и сила тока (при неизменном напряжении). Это и означает увеличение сопротивления.
Как опять-таки показывает опыт, зависимость сопротивления \(R\) металлического проводника от температуры \(t\) с хорошей точностью является линейной:
\(R = R_0(1 + \alpha t).\) (1)
Здесь \(R_0\) — сопротивление проводника при \(0^{\circ}\rm C\). График зависимости (1) является прямой линией (рис. 4).

Рис. 4. \(R = R(t)\)
Множитель \(\alpha\) называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.
Длина проводника \(l\) и его площадь поперечного сечения \(S\) при изменении температуры меняются несущественно. Выразим \(R\) и \(R_0\) через удельное сопротивление:
\(R = \rho \frac{\displaystyle l}{\displaystyle S \vphantom{1^a}}, \ \ R_0 = \rho_0 \frac{\displaystyle l}{\displaystyle S \vphantom{1^a}},\)
и подставим эти формулы в (1). Получим аналогичную зависимость удельного сопротивления от температуры:
\(\rho = \rho_0(1 + \alpha t).\)
Коэффициент \(\alpha\) весьма мал (для меди, например, \(\alpha = 0,0043\)), так что температурной зависимостью сопротивления металла часто можно пренебречь. Однако в ряде случаев считаться с ней приходиться. Например, вольфрамовая спираль электрической лампочки раскаляется до такой степени, что её вольт-амперная характеристика оказывается существенно нелинейной.
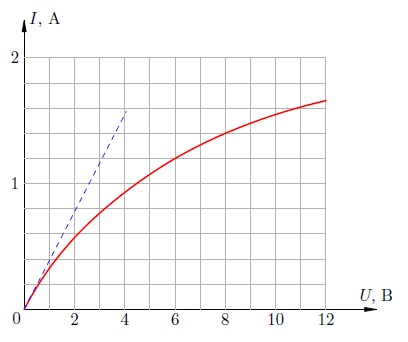
Рис. 5. Вольт-амперная характеристика лампочки
Так, на рис. 5 приведена вольт-амперная характеристика автомобильной лампочки. Если бы лампочка представляла собой идеальный резистор, её вольт-амперная характеристика была прямой линией в соответствии с законом Ома. Эта прямая изображена синим пунктиром.
Однако по мере роста напряжения, приложенного к лампочке, график отклоняется от этой прямой всё сильнее и сильнее. Почему? Дело в том, что с увеличением напряжения ток через лампочку возрастает и больше разогревает спираль; сопротивление спирали поэтому также увеличивается. Следовательно, сила тока хотя и продолжит возрастать, но будет иметь всё меньшее и меньшее значение по сравнению с тем, которое предписывается «пунктирной» линейной зависимостью тока от напряжения.
Разберем задание из вариантов ЕГЭ по физике по теме «Электрический ток в металлах, металлы и диэлектрики в электрическом поле».
Задача 1.
Два незаряженных пластмассовых кубика 1 и 2 сблизили вплотную и поместили в электрическое поле, напряжённость которого направлена горизонтально вправо, как показано в левой части рисунка. То же самое проделали с двумя незаряженными стальными кубиками 3 и 4. Затем кубики быстро раздвинули и уже потом убрали электрическое поле (правая часть рисунка).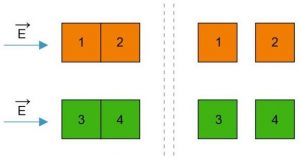
Выберите два верных утверждения, описывающих данный процесс.
1) После разделения кубик 3 имеет отрицательный заряд.
2) При помещении пластмассовых кубиков в электрическое поле наблюдается явление поляризации.
3) В электрическом поле кубики 1 и 2 приобретают суммарный отрицательный заряд.
4) В электрическом поле кубики 3 и 4 приобретают суммарный отрицательный заряд.
5) После разделения кубик 2 имеет положительный заряд.
Решение:
Пластмассовые кубики 1 и 2 – диэлектрики. При помещении их в однородное электростатическое поле в них происходит поляризация – поворот молекул вдоль силовых линий поля. Утверждение 2 – верное. При этом эти кубики не приобретают никакого заряда и после отключения поля возвращаются в исходное состояние, оставаясь незаряженными. Утверждения 3 и 5 – неверные.
Кубики 3 и 4 стальные, то есть металлические. В них происходит перераспределение электронов – электризация. При этом электроны смещаются против силовой линии, то есть влево. Поэтому кубик 3 приобретает отрицательный заряд, так как в нём будет избыток электронов. А кубик 4 приобретает положительный заряд, так как в нём будет недостаток электронов. Суммарный же заряд остаётся неизменным и равным нулю, каким он и был до включения поля, по закону сохранения заряда. Утверждение 1 – верное. Утверждение 4 – неверное.
Ответ:
- 1
- 2
Задача 2.
Два незаряженных алюминиевых кубика 1 и 2 сблизили вплотную и поместили в электрическое поле, напряжённость которого направлена горизонтально вправо, как показано в левой части рисунка. То же самое проделали с двумя незаряженными эбонитовыми кубиками 3 и 4. Затем кубики быстро раздвинули и уже потом убрали электрическое поле (правая часть рисунка).
Выберите два верных утверждения, описывающих данный процесс.
1) После разделения кубик 3 имеет отрицательный заряд.
2) В электрическом поле кубики 1 и 2 приобретают суммарный отрицательный заряд.
3) При помещении алюминиевых кубиков в электрическое поле в них происходит
перераспределение свободных электронов.
4) В электрическом поле кубики 3 и 4 приобретают суммарный отрицательный заряд.
5) После разделения кубик 2 имеет положительный заряд.
Решение:
Алюминиевые кубики 1 и 2 – проводники. В них происходит перераспределение электронов – электризация. При этом электроны смещаются против силовой линии, то есть влево. Поэтому кубик 1 приобретает отрицательный заряд, так как в нём будет избыток электронов. А кубик 2 приобретает положительный заряд, так как в нём будет недостаток электронов. Суммарный же заряд остаётся неизменным и равным нулю, каким он и был до включения поля, по закону сохранения заряда. Утверждение 2 – неверное. Утверждение 3 – верное. Утверждение 5 – верное.
Кубики 3 и 4 эбонитовые, то есть диэлектрики. При помещении их в однородное электростатическое поле в них происходит поляризация – поворот молекул вдоль силовых линий поля. При этом эти кубики не приобретают никакого заряда и после отключения поля возвращаются в исходное состояние, оставаясь незаряженными. Утверждения 1 и 4 – неверные.
Ответ:
- 3
- 5




























