Интерференция волн.

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: интерференция света.

В предыдущем листке, посвящённом принципу Гюйгенса, мы говорили о том, что общая картина волнового процесса создаётся наложением вторичных волн. Но что это значит - "наложением"? В чём состоит конкретный физический смысл наложения волн? Что вообще происходит, когда в пространстве одновременно распространяются несколько волн? Этим вопросам и посвящён данный листок.

к оглавлению ▴

Сложение колебаний.

 

Сейчас мы будем рассматривать взаимодействие двух волн. Природа волновых процессов роли не играет - это могут быть механические волны в упругой среде или электромагнитные волны (в частности, свет) в прозрачной среде или в вакууме.

Опыт показывает, что волны складываются друг с другом в следующем смысле.

Принцип суперпозиции. Если две волны накладываются друг на друга в определённой области пространства, то они порождают новый волновой процесс. При этом значение колеблющейся величины в любой точке данной области равно сумме соответствующих колеблющихся величин в каждой из волн по отдельности.

Например, при наложении двух механических волн перемещение частицы упругой среды равно сумме перемещений, создаваемых в отдельности каждой волной. При наложении двух электромагнитных волн напряжённость электрического поля в данной точке равна сумме напряжённостей в каждой волне (и то же самое для индукции магнитного поля).

Разумеется, принцип суперпозиции справедлив не только для двух, но и вообще для любого количества накладывающихся волн. Результирующее колебание в данной точке всегда равно сумме колебаний, создаваемых каждой волной по отдельности.

Мы ограничимся рассмотрением наложения двух волн одинаковой амплитуды и частоты. Этот случай наиболее часто встречается в физике и, в частности, в оптике.

Оказывается, на амплитуду результирующего колебания сильно влияет разность фаз складывающихся колебаний. В зависимости от разности фаз в данной точке пространства две волны могут как усиливать друг друга, так и полностью гасить!

Предположим, например, что в некоторой точке фазы колебаний в накладывающихся волнах совпадают (рис. 1).

Рис. 1. Волны в фазе: усиление колебаний

 

Мы видим, что максимумы красной волны приходятся в точности на максимумы синей волны, минимумы красной волны - на минимумы синей (левая часть рис. 1). Складываясь в фазе, красная и синяя волны усиливают друг друга, порождая колебания удвоенной амплитуды (справа на рис. 1).

Теперь сдвинем синюю синусоиду относительно красной на половину длины волны. Тогда максимумы синей волны будут совпадать с минимумами красной и наоборот - минимумы синей волны совпадут с максимумами красной (рис. 2, слева).

Рис. 2. Волны в противофазе: гашение колебаний

 

Колебания, создаваемые этими волнами, будут происходить, как говорят, в противофазе - разность фаз колебаний станет равна \(\pi\). Результирующее колебание окажется равным нулю, т. е. красная и синяя волны попросту уничтожат друг друга (рис. 2, справа).

к оглавлению ▴

Когерентные источники.

 

Пусть имеются два точечных источника, создающие волны в окружающем пространстве. Мы полагаем, что эти источники согласованы друг с другом в следующем смысле.

Когерентность. Два источника называются когерентными, если они имеют одинаковую частоту и постоянную, не зависящую от времени разность фаз. Волны, возбуждаемые такими источниками, также называются когерентными.

Итак, рассматриваем два когерентных источника \(S_{1}\) и \(S_{2}\). Для простоты считаем, что источники излучают волны одинаковой амплитуды, а разность фаз между источниками равна нулю. В общем, эти источники являются "точными копиями" друг друга (в оптике, например, источник \(S_{2}\) служит изображением источника \(S_{1}\) в какой-либо оптической системе).

Наложение волн, излучённых данными источниками, наблюдается в некоторой точке \(P\). Вообще говоря, амплитуды этих волн в точке \(P\) не будут равны друг другу - ведь, как мы помним, амплитуда сферической волны обратно пропорциональна расстоянию до источника, и при разных расстояниях \(S_{1}P\) и \(S_{2}P\) амплитуды пришедших волн окажутся различными. Но во многих случаях точка \(P\) расположена достаточно далеко от источников - на расстоянии гораздо большем, чем расстояние между самими источниками. В такой ситуации различие в расстояниях \(S_{1}P\) и \(S_{2}P\) не приводит к существенному отличию в амплитудах приходящих волн. Следовательно, мы можем считать, что амплитуды волн в точке \(P\) также совпадают.

к оглавлению ▴

Условие максимума и минимума.

 

Однако величина \(d=|S_{1}P-S_{2}P|\), называемая разностью хода, имеет важнейшее значение. От неё самым решительным образом зависит то, какой результат сложения приходящих волн мы увидим в точке \(P\).

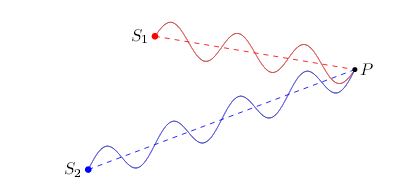Рис. 3. Усиление колебаний в точке P

 

В ситуации на рис. 3 разность хода равна длине волны \((d=\lambda )\). Действительно, на отрезке \(S_{1}P\) укладываются три полных волны, а на отрезке \(S_{2}P\) - четыре (это, конечно, лишь иллюстрация; в оптике, например, длина таких отрезков составляет порядка миллиона длин волн). Легко видеть, что волны в точке \(P\) складываются в фазе и создают колебания удвоенной амплитуды - наблюдается, как говорят, интерференционный максимум.

Ясно, что аналогичная ситуация возникнет при разности хода, равной не только длине волны, но и любому целому числу длин волн.

Условие максимума. При наложении когерентных волн колебания в данной точке будут иметь максимальную амплитуду, если разность хода равна целому числу длин волн:

\(d=n\lambda (n=0,1,2,,...).\) (1)

Теперь посмотрим на рис. 4. На отрезке \(S_{1}P\) укладываются две с половиной волны, а на отрезке \(S_{2}P\) -три волны. Разность хода составляет половину длины волны (d=\lambda /2\)).

Рис. 4. Гашение колебаний в точке P

 

Теперь нетрудно видеть, что волны в точке \(P\) складываются в противофазе и гасят друг друга - наблюдается интерференционный минимум. То же самое будет, если разность хода окажется равна половине длины волны плюс любое целое число длин волн.

Условие минимума.
Когерентные волны, складываясь, гасят друг друга, если разность хода равна полуцелому числу длин волн:

\(d=n\lambda+\frac{\displaystyle \lambda }{\displaystyle 2}.\) (2)

Равенство (2) можно переписать следующим образом:

\(d=(2n+1)\frac{\displaystyle \lambda }{\displaystyle 2}\).

Поэтому условие минимума формулируют ещё так: разность хода должна быть равна нечётному числу длин полуволн.

к оглавлению ▴

Интерференционная картина.

 

А что, если разность хода принимает какое-то иное значение, не равное целому или полуцелому числу длин волн? Тогда волны, приходящие в данную точку, создают в ней колебания с некоторой промежуточной амплитудой, расположенной между нулём и удвоенным значением 2A амплитуды одной волны. Эта промежуточная амплитуда может принимать все значения от 0 до 2A по мере того, как разность хода меняется от полуцелого до целого числа длин волн.

Таким образом, в той области пространства, где происходит наложение волн когерентных источников \(S_{1}\) и \(S_{2}\) , наблюдается устойчивая интерференционная картина - фиксированное не зависящее от времени распределение амплитуд колебаний. А именно, в каждой точке \(S_{1}P\) данной области амплитуда колебаний принимает своё значение, определяемое разностью хода \(d=|S_{1}P-S_{2}P|\) приходящих сюда волн, и это значение амплитуды не меняется со временем.

Такая стационарность интерференционной картины обеспечивается когерентностью источников. Если, например, разность фаз источников будет постоянно меняться, то никакой устойчивой интерференционной картины уже не возникнет.

Теперь, наконец, мы можем сказать, что такое интерференция.

Интерференция - это взаимодействие волн, в результате которого возникает устойчивая интерференционная картина, то есть не зависящее от времени распределение амплитуд результирующих колебаний в точках области, где волны накладываются друг на друга.

Если волны, перекрываясь, образуют устойчивую интерференционную картину, то говорят попросту, что волны интерферируют. Как мы выяснили выше, интерферировать могут только когерентные волны. Когда, например, разговаривают два человека, то мы не замечаем вокруг них чередований максимумов и минимумов громкости; интерференции нет, поскольку в данном случае источники некогерентны.

На первый взгляд может показаться, явление интерференции противоречит закону сохранения энергии - например, куда девается энергия, когда волны полностью гасят друг друга? Но никакого нарушения закона сохранения энергии, конечно же, нет: энергия просто перераспределяется между различными участками интерференционной картины. Наибольшее количество энергии концентрируется в интерференционных максимумах, а в точки интерференционных минимумов энергия не поступает совсем.

На рис. 5 показана интерференционная картина, созданная наложением волн двух точечных источников \(S_{1}\) и \(S_{2}\). Картина построена в предположении, что область наблюдения интерференции находится достаточно далеко от источников. Пунктиром отмечена ось симметрии интерференционной картины.

Рис. 5. Интерференция волн двух точечных источников

 

Цвета точек интерференционной картины на этом рисунке меняются от чёрного до белого через промежуточные оттенки серого. Чёрный цвет - интерференционные минимумы, белый цвет - интерференционные максимумы; серый цвет - промежуточное значение амплитуды, и чем больше амплитуда в данной точке, тем светлее сама точка.

Обратите внимание на прямую белую полосу, которая идёт вдоль оси симметрии картины. Здесь расположены так называемые центральные максимумы. Действительно, любая точка данной оси равноудалена от источников (разность хода равна нулю), так что в этой точке будет наблюдаться является интерференционный максимум.

Остальные белые полосы и все чёрные полосы слегка искривлены; можно показать, что они являются ветвями гипербол. Однако в области, расположенной на большом расстоянии от источников, кривизна белых и чёрных полос мало заметна, и выглядят эти полосы почти прямыми.

к оглавлению ▴

Интерференционный опыт, изображённый на рис. 5, вместе с соответствующим методом расчёта интерференционной картины называется схемой Юнга. Эта схема лежит в основе знаменитного
опыта Юнга (речь о котором пойдёт в теме Дифракция света). Многие эксперименты по интерференции света так или иначе сводятся к схеме Юнга.

В оптике интерференционную картину обычно наблюдают на экране. Давайте ещё раз посмотрим на рис. 5 и представим себе экран, поставленный перпендикулярно пунктирной оси.
На этом экране мы увидим чередование светлых и тёмных интерференционных полос.

На рис. 6 синусоида показывает распределение освещённости вдоль экрана. В точке O, расположенной на оси симметрии, находится центральный максимум. Первый максимум в верхней части экрана, соседний с центральным, находится в точке A. Выше идут второй, третий (и такдалее) максимумы.

Рис. 6. Интерференционная картина на экране

 

Расстояние \(\Delta x=OA\), равное расстоянию между любыми двумя соседними максимумами или минимумами, называется шириной интерференционной полосы. Сейчас мы займёмся нахождением этой величины.

Пусть источники находятся на расстоянии \(a\) друг от друга, а экран расположен на расстоянии \(L\) от источников (рис. 7 ). Экран заменён осью \(OX\); начало отсчёта \(O\), как и выше, отвечает центральному максимуму.

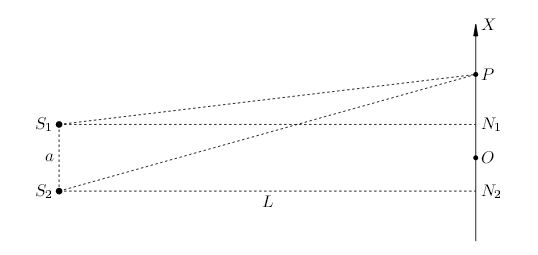Рис. 7. Вычисление координат максимумов

 

Точки \(N_{1}\) и \(N_{2}\) служат проекциями точек \(S_{1}\) и \(S_{2}\) на ось \(OX\) и расположены симметрично относительно точки \(O\). Имеем: \(ON_{1}=ON_{2}=a/2\).

Точка наблюдения \(P\) может находиться на оси \(OX\) (на экране) где угодно. Координату точки
\(P\) мы обозначим \(x\). Нас интересует, при каких значениях \(x\) в точке \(P\) будет наблюдаться интерференционный максимум.

Волна, излучённая источником \(S_{1}\), проходит расстояние:

\(S_{1}P=\sqrt{\displaystyle S_{\displaystyle 1}N_{\displaystyle 1}^{\displaystyle 2}+PN_{\displaystyle 1}^{\displaystyle 2}}=\sqrt{L^{2}+(x-\frac{\displaystyle a}{\displaystyle 2})^{\displaystyle 2}}=L\sqrt{1+(\frac{\displaystyle 2x-a}{\displaystyle 2L})^{\displaystyle 2}}\). (3)

Теперь вспомним, что расстояние между источниками много меньше расстояния от источников до экрана: \(a\leq L\). Кроме того, в подобных интерференционных опытах координата \(x\) точки наблюдения также гораздо меньше \(L\). Это означает, что второе слагаемое под корнем в выражении (3) много меньше единицы:

\((\frac{\displaystyle 2x-a}{\displaystyle 2L})^{\displaystyle 2}\leq 1\).

Раз так, можно использовать приближённую формулу:

\(\sqrt{1+\alpha }=1+\frac{\displaystyle \alpha }{\displaystyle 2}, \alpha \leq 1\) (4)

Применяя её к выражению (4), получим:

\(S_{1}P=L(1+\frac{1}{2}(\frac{\displaystyle 2x-a}{\displaystyle 2L})^{\displaystyle 2})=L+\frac{(\displaystyle 2x-a)^{\displaystyle 2}}{\displaystyle 8L}\) (5)

Точно так же вычисляем расстояние, которое проходит волна от источника \(S_{2}\) до точки наблюдения:

\(S_{2}P=\sqrt{\displaystyle S_{\displaystyle 1}N_{\displaystyle 2}^{\displaystyle 2}+PN_{\displaystyle 2}^{\displaystyle 2}}=\sqrt{L^{2}+(x+\frac{\displaystyle a}{\displaystyle 2})^{\displaystyle 2}}=L\sqrt{1+(\frac{\displaystyle 2x+a}{\displaystyle 2L})^{\displaystyle 2}}\). (6)

Применяя к выражению (6) приближённую формулу (4), получаем:

\(S_{2}P=L(1+\frac{1}{2}(\frac{\displaystyle 2x+a}{\displaystyle 2L})^{\displaystyle 2})=L+\frac{(\displaystyle 2x+a)^{\displaystyle 2}}{\displaystyle 8L}\). (7)

Вычитая выражения (7) и (5), находим разность хода:

\(d=S_{2}P-S_{1}P=\frac{(\displaystyle 2x+a)^{\displaystyle 2}-(\displaystyle 2x-a)^{\displaystyle 2}}{\displaystyle 8L}=\frac{\displaystyle ax}{\displaystyle L}\). (8)

Пусть \(\lambda \) - длина волны, излучаемой источниками. Согласно условию (1), в точке \(P\) будет наблюдаться интерференционный максимум, если разность хода равна целому числу длин волн:

\(d=\frac{\displaystyle ax}{\displaystyle L}=n\lambda (n=0,1,2,3,...).\)

Отсюда получаем координаты максимумов в верхней части экрана (в нижней части максимумы идут симметрично):

\(\displaystyle x_{\displaystyle n}=\frac{\displaystyle n\lambda L}{\displaystyle a} (n=0,1,2,3,...).\)

При \(n=0\) получаем, разумеется, \(\displaystyle x_{\displaystyle n}=0\) (центральный максимум). Первый максимум рядом с центральным соответствует значению \(n=1\) и имеет координату \(\displaystyle x_{\displaystyle 1}=\lambda L/a\).Такой же будет и ширина интерференционной полосы:

\(\Delta x=\displaystyle x_{\displaystyle n+1}-\displaystyle x_{\displaystyle n}=\frac{(\displaystyle n+\displaystyle 1)\lambda L}{\displaystyle a}-\frac{\displaystyle n\lambda L}{\displaystyle a}=\frac{\displaystyle \lambda L}{\displaystyle a}\).