Линзы. Ход лучей.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: линзы

Преломление света широко используется в различных оптических приборах: фотоаппаратах, биноклях, телескопах, микроскопах. . . Непременной и самой существенной деталью таких приборов является линза.

Линза - это оптически прозрачное однородное тело, ограниченное с двух сторон двумя сферическими (или одной сферической и одной плоской) поверхностями.

Линзы обычно изготавливаются из стекла или специальных прозрачных пластмасс. Говоря о материале линзы, мы будем называть его стеклом - особой роли это не играет.

Двояковыпуклая линза.

Рассмотрим сначала линзу, ограниченную с обеих сторон двумя выпуклыми сферическими поверхностями (рис. 1). Такая линза называется двояковыпуклой. Наша задача сейчас - понять ход лучей в этой линзе.

Рис. 1. Преломление в двояковыпуклой линзе

Проще всего обстоит дело с лучом, идущим вдоль главной оптической оси - оси симметрии линзы. На рис. 1 этот луч выходит из точки . Главная оптическая ось перпендикулярна обеим сферическим поверхностям, поэтому данный луч идёт сквозь линзу, не преломляясь.

Теперь возьмём луч , идущий параллельно главной оптической оси. В точке падения
луча на линзу проведена нормаль к поверхности линзы; поскольку луч переходит из воздуха в оптически более плотное стекло, угол преломления меньше угла падения . Следовательно, преломлённый луч приближается к главной оптической оси.

В точке выхода луча из линзы также проведена нормаль . Луч переходит в оптически менее плотный воздух, поэтому угол преломления больше угла падения ; луч
преломляется опять-таки в сторону главной оптической оси и пересекает её в точке .

Таким образом, всякий луч, параллельный главной оптической оси, после преломления в линзе приближается к главной оптической оси и пересекает её. На рис. 2 изображена картина преломления достаточно широкого светового пучка, параллельного главной оптической оси.

Рис. 2. Сферическая аберрация в двояковыпуклой линзе

Как видим, широкий пучок света не фокусируется линзой: чем дальше от главной оптической оси расположен падающий луч, тем ближе к линзе он пересекает главную оптическую ось после преломления. Это явление называется сферической аберрацией и относится к недостаткам линз - ведь хотелось бы всё же, чтобы линза сводила параллельный пучок лучей в одну точку.

Весьма приемлемой фокусировки можно добиться, если использовать узкий световой пучок, идущий вблизи главной оптической оси. Тогда сферическая аберрация почти незаметна - посмотрите на рис. 3.

Рис. 3. Фокусировка узкого пучка собирающей линзой

Хорошо видно, что узкий пучок, параллельный главной оптической оси, после прохождения линзы собирается приблизительно в одной точке . По этой причине наша линза носит название собирающей.

Точка называется фокусом линзы. Вообще, линза имеет два фокуса, находящиеся на главной оптической оси справа и слева от линзы. Расстояния от фокусов до линзы не обязательно равны друг другу, но мы всегда будем иметь дело с ситуациями, когда фокусы расположены симметрично относительно линзы.

Двояковогнутая линза.

Теперь мы рассмотрим совсем другую линзу, ограниченную двумя вогнутыми сферическими поверхностями (рис. 4). Такая линза называется двояковогнутой. Так же, как и выше, мы проследим ход двух лучей, руководствуясь законом преломления.

Рис. 4. Преломление в двояковогнутой линзе

Луч, выходящий из точки и идущий вдоль главной оптической оси, не преломляется - ведь главная оптическая ось, будучи осью симметрии линзы, перпендикулярна обеим сферическим поверхностям.

Луч , параллельный главной оптической оси, после первого преломления начинает удаляться от неё (так как при переходе из воздуха в стекло ), а после второго преломления удаляется от главной оптической оси ещё сильнее (так как при переходе из стекла в воздух ).

Двояковогнутая линза преобразует параллельный пучок света в расходящийся пучок (рис. 5) и называется поэтому рассеивающей.

Здесь также наблюдается сферическая аберрация: продолжения расходящихся лучей не пересекаются в одной точке. Мы видим, что чем дальше от главной оптической оси расположен падающий луч, тем ближе к линзе пересекает главную оптическую ось продолжение преломлённого луча.

Как и в случае двояковыпуклой линзы, сферическая аберрация будет практически незаметна для узкого приосевого пучка (рис. 6). Продолжения лучей, расходящихся от линзы, пересекаются приблизительно в одной точке - в фокусе линзы .

Если такой расходящийся пучок попадёт в наш глаз, то мы увидим за линзой светящуюся точку! Почему? Вспомните, как возникает изображение в плоском зеркале: наш мозг обладает способностью продолжать расходящиеся лучи до их пересечения и создавать в месте пересечения иллюзию светящегося объекта (так называемое мнимое изображение). Вот именно такое мнимое изображение, расположенное в фокусе линзы, мы и увидим в данном случае.

Рис. 5. Сферическая аберрация в двояковогнутой линзе

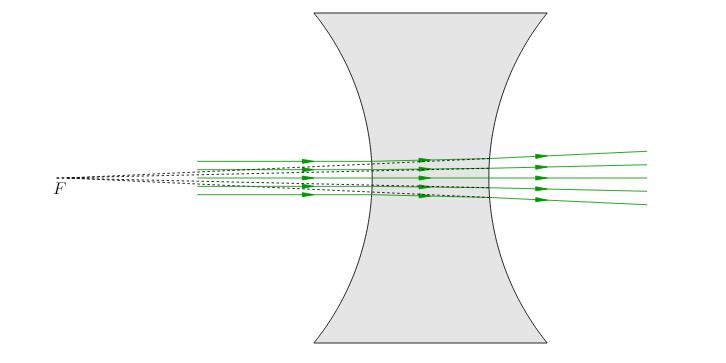Рис. 6. Преломление узкого пучка в рассеивающей линзе

Виды собирающих и рассеивающих линз.

Мы рассмотрели две линзы: двояковыпуклую линзу, которая является собирающей, и двояковогнутую линзу, которая является рассеивающей. Существуют и другие примеры собирающих и рассеивающих линз.

Полный набор собирающих линз представлен на рис. 7.

Помимо известной нам двояковыпуклой линзы, здесь изображены:плосковыпуклая линза, у которой одна из поверхностей плоская, и вогнуто-выпуклая линза, сочетающая вогнутую и выпуклую граничные поверхности. Обратите внимание, что у вогнуто-выпуклой линзы выпуклая поверхность в большей степени искривлена (радиус её кривизны меньше); поэтому собирающее действие выпуклой преломляющей поверхности перевешивает рассеивающее действие вогнутой поверхности, и линза в целом оказывается собирающей.

Все возможные рассеивающие линзы изображены на рис. 8.

Наряду с двояковогнутой линзой мы видим плосковогнутую (одна из поверхностей которой плоская) и выпукло-вогнутую линзу. Вогнутая поверхность выпукло-вогнутой линзы искривлена в большей степени, так что рассеивающее действие вогнутой границы преобладает над собирающим действием выпуклой границы, и в целом линза оказывается рассеивающей.

Рис. 7. Собирающие линзы

Рис. 8. Рассеивающие линзы

Попробуйте самостоятельно построить ход лучей в тех видах линз, которые мы не рассмотрели, и убедиться, что они действительно являются собирающими или рассеивающими. Это отличное упражнение, и в нём нет ничего сложного - ровно те же самые построения, которые мы проделали выше!