Отражение света.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: закон отражения света, построение изображений в плоском зеркале.
Когда световой луч падает на границу раздела двух сред, происходит отражение света: луч изменяет направление своего хода и возвращается в исходную среду.
На рис. 1 изображены падающий луч \(AO\), отражённый луч \(OB\), а также перпендикуляр \(OC\), проведённый к отражающей поверхности \(KL\) в точке падения \(O\).
 |
| Рис. 1. Закон отражения |
Угол \(AOC\) называется углом падения. Обратите внимание и запомните: угол падения отсчитывается от перпендикуляра к отражающей поверхности, а не от самой поверхности! Точно так же угол отражения - это угол \(BOC\), образованный отражённым лучом и перпендикуляром к поверхности.
Закон отражения.
Сейчас мы сформулируем один из самых древних законов физики. Он был известен грекам ещё в античности!
Закон отражения.
1) Падающий луч, отражённый луч и перпендикуляр к отражающей поверхности, проведённый в точке падения, лежат в одной плоскости.
2) Угол отражения равен углу падения.
Таким образом, \(\angle AOC=\angle BOC\), что и показано на рис. 1.
Закон отражения имеет одно простое, но очень важное геометрическое следствие. Давайте посмотрим на рис. 2. Пусть из точки \(A\) исходит световой луч. Построим точку \({A}'\), симметричную точке \(A\) относительно отражающей поверхности \(KL\).
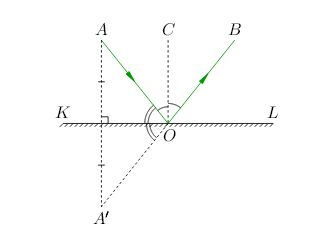 |
| Рис. 2. Отражённый луч выходит из точки \({A}'\) |
Из симметрии точек \(A\) и \({A}'\) ясно, что \(\angle AOK=\angle {A}'OK\). Кроме того, \(\angle AOK+\angle AOC=90^{\circ}\). Поэтому \(\angle {A}'OB=2(\angle AOK+\angle AOC)=180^{\circ}\), и, следовательно, точки \({A}', O , B\) лежат на одной прямой! Отражённый луч \(OB\) как бы выходит из точки \({A}'\), симметричной точке \(A\) относительно отражающей поверхности. Данный факт нам чрезвычайно пригодится в самом скором времени.
Закон отражения описывает ход отдельных световых лучей - узких пучков света. Но во многих случаях пучок является достаточно широким, то есть состоит из множества параллельных лучей. Картина отражения широкого пучка света будет зависеть от свойств отражающей поверхности.
Если поверхность является неровной, то после отражения параллельность лучей нарушится. В качестве примера на рис. 3 показано отражение от волнообразной поверхности. Отражённые лучи, как видим, идут в самых разных направлениях.
 |
| Рис. 3. Отражение от волнообразной поверхности |
Но что значит "неровная" поверхность? Какие поверхности являются "ровными"? Ответ таков: поверхность считается неровной, если размеры её неровностей не меньше длины световых волн. Так, на рис. 3 характерный размер неровностей на несколько порядков превышает величину длин волн видимого света.
Поверхность с микроскопическими неровностями, соизмеримыми с длинами волн видимого света, называется матовой. В результате отражения параллельного пучка от матовой поверхности получается рассеянный свет - лучи такого света идут во всевозможных направлениях. (Именно поэтому мы видим окружающие предметы: они отражают рассеянный свет, который мы и наблюдаем с любого ракурса.)
Само отражение от матовой поверхности называется поэтому рассеянным или диффузным. (Латинское слово diffusio как раз и означает распространение, растекание, рассеивание.)
Если же размер неровностей поверхности меньше длины световой волны, то такая поверхность называется зеркальной. При отражении от зеркальной поверхности параллельность пучка сохраняется: отражённые лучи также идут параллельно (рис. 4)
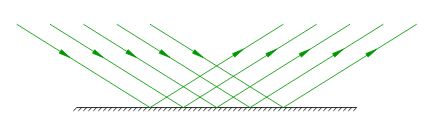 |
| Рис. 4. Отражение от зеркальной поверхности |
Приблизительно зеркальной является гладкая поверхность воды, стекла или отполированного металла. Отражение от зеркальной поверхности называется соответственно зеркальным. Нас будет интересовать простой, но важный частный случай зеркального отражения - отражение в плоском зеркале.
Плоское зеркало.
Плоское зеркало - это часть плоскости, зеркально отражающая свет. Плоское зеркало - привычная вещь; таких зеркал несколько в вашем доме. Но теперь мы сможем разобраться, почему, смотрясь в зеркало, вы видите в нём отражение себя и находящихся рядом с вами предметов.
Точечный источник света \(S\) на рис. 5 испускает лучи в разных направлениях; давайте возьмём два близких луча, падающих на плоское зеркало. Мы уже знаем, что отражённые лучи пойдут так, будто они исходят из точки \(S{}'\) , симметричной точке \(S\) относительно плоскости зеркала.
 |
| Рис. 5. Изображение источника света в плоском зеркале |
Самое интересное начинается, когда расходящиеся отражённые лучи попадают к нам в глаз. Особенность нашего сознания состоит в том, что мозг достраивает расходящийся пучок, продолжая его за зеркало до пересечения в точке \(S{}'\). Нам кажется, что отражённые лучи исходят из точки \(S{}'\) - мы видим там светящуюся точку!
Эта точка служит изображением источника света \(S\) Конечно, в реальности ничего за зеркалом не светится, никакая энергия там не сосредоточена - это иллюзия, обман зрения, порождение нашего сознания. Поэтому точка \(S{}'\) называется мнимым изображением источника \(S\). В точке \(S{}'\) пересекаются не сами световые лучи, а их мысленные продолжения "в зазеркалье".
Ясно, что изображение \(S{}'\) будет существовать независимо от размеров зеркала и от того, находится ли источник непосредственно над зеркалом или нет (рис. 6). Важно только, что-бы отражённые от зеркала лучи попадали в глаз - а уж глаз сам сформирует изображение источника.
 |
| Рис. 6. Источник не над зеркалом: изображение есть всё равно |
От расположения источника и размеров зеркала зависит область видения - пространственная область, из которой видно изображение источника. Область видения задаётся краями \(K\) и \(L\) зеркала \(KL\). Построение области видения изображения \(S{}'\) ясно из рис. 7; искомая область видения выделена серым фоном.
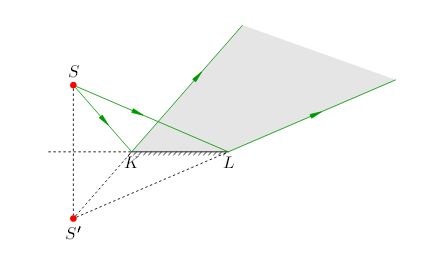 |
| Рис. 7. Область видения изображения источника S |
Как построить изображение произвольного предмета в плоском зеркале? Для этого достаточно найти изображение каждой точки этого предмета. Но мы знаем, что изображение точки симметрично самой точке относительно зеркала. Следовательно, изображение предмета в плоском зеркале симметрично предмету относительно плоскости зеркала (рис. 8).
 |
| Рис. 8. Изображение предмета AB в плоском зеркале |
Расположение предмета относительно зеркала и размеры самого зеркала не влияют на изображение (рис. 9).
 |
| Рис. 9. Изображение не зависит от взаимного расположения предмета и зеркала |

































