Преломление света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.

На границе раздела двух прозрачных сред наряду с отражением света наблюдается его преломление - свет, переходя в другую среду, меняет направление своего распространения.

Преломление светового луча происходит при его наклонном падении на поверхность раздела (правда, не всегда - читайте дальше про полное внутреннее отражение). Если же луч падает перпендикулярно поверхности, то преломления не будет - во второй среде луч сохранит своё направление и также пойдёт перпендикулярно поверхности.

Закон преломления (частный случай).

Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.

Предположим, что луч света, идущий в воздухе, наклонно падает на поверхность стекла, воды или какой-либо другой прозрачной среды. При переходе в среду луч преломляется, и его дальнейший ход показан на рис. 1.

Рис. 1. Преломление луча на границе "воздух–среда"

В точке падения \(O\) проведён перпендикуляр (или, как ещё говорят, нормаль) \(CD\) к поверхности среды. Луч \(AO\), как и раньше, называется падающим лучом, а угол \(\alpha \) между падающим лучом и нормалью - углом падения. Луч \(OB\) - это преломлённый луч; угол \(\beta \) между преломлённым лучом и нормалью к поверхности называется углом преломления.

Всякая прозрачная среда характеризуется величиной \(n\), которая называется показателем преломления этой среды. Показатели преломления различных сред можно найти в таблицах. Например, для стекла \(n=1,6\), а для воды \(n=1,33\). Вообще, у любой среды \(n \textgreater 1\); показатель преломления равен единице только в вакууме. У воздуха \(n=1,0003\), поэтому для воздуха с достаточной точностью можно полагать в задачах \(n=1\) (в оптике воздух не сильно отличается от вакуума).

Закон преломления (переход "воздух–среда").

1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:

\(\frac{\displaystyle sin\alpha }{\displaystyle sin\beta }=n\). (1)

Поскольку \(n \textgreater 1\) из соотношения (1) следует, что \(sin\alpha \textgreater sin\beta \), то есть \(\alpha \textgreater \beta \) - угол преломления меньше угла падения. Запоминаем: переходя из воздуха в среду, луч после преломления идёт ближе к нормали.

Показатель преломления непосредственно связан со скоростью \(v\) распространения света в данной среде. Эта скорость всегда меньше скорости света в вакууме: \(v \textless c\). И вот оказывается,что

\(n=\frac{\displaystyle c }{\displaystyle v }\). (2)

Почему так получается, мы с вами поймём при изучении волновой оптики. А пока скомбинируем формулы . (1) и (2):

\(\frac{\displaystyle sin\alpha }{\displaystyle sin\beta }=\frac{\displaystyle c }{\displaystyle v }\). (3)

Так как показатель преломления воздуха очень близок единице, мы можем считать, что скорость света в воздухе примерно равна скорости света в вакууме \(c\). Приняв это во внимание и глядя на формулу . (3), делаем вывод: отношение синуса угла падения к синусу угла преломления равно отношению скорости света в воздухе к скорости света в среде.

Обратимость световых лучей.

Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.

Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.

Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.

Рис. 2. Преломление луча на границе "среда–воздух"

Раз геометрическая картинка не изменилась, той же самой останется и формула (1): отношение синуса угла \(\alpha\) к синусу угла \(\beta \) по-прежнему равно показателю преломления среды. Правда, теперь углы поменялись ролями: угол \(\beta \) стал углом падения, а угол \(\alpha\) - углом преломления.

В любом случае, как бы ни шёл луч - из воздуха в среду или из среды в воздух - работает следующее простое правило. Берём два угла - угол падения и угол преломления; отношение синуса большего угла к синусу меньшего угла равно показателю преломления среды.

Теперь мы целиком подготовлены для того, чтобы обсудить закон преломления в самом общем случае.

Закон преломления (общий случай).

Пусть свет переходит из среды 1 с показателем преломления \(n_{\displaystyle 1}\) в среду 2 с показателем преломления \(n_{\displaystyle 2}\). Среда с большим показателем преломления называется оптически более плотной; соответственно, среда с меньшим показателем преломления называется оптически менее плотной.

Переходя из оптически менее плотной среды в оптически более плотную, световой луч после преломления идёт ближе к нормали (рис. 3). В этом случае угол падения больше угла преломления: \(\alpha \textgreater \beta \).

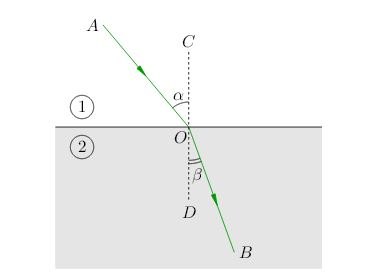Рис. 3. \(n_{1} \textless n_{2}\Rightarrow \alpha \textgreater \beta \)

Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4). Здесь угол падения меньше угла преломления: \(\alpha \textless \beta \)

Рис. 4. \(n_{1} \textgreater n_{2}\Rightarrow \alpha \textless \beta \)

Оказывается, оба этих случая охватываются одной формулой - общим законом преломления, справедливым для любых двух прозрачных сред.

Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:

\(\frac{\displaystyle sin\alpha }{\displaystyle sin\beta }=\frac{\displaystyle n_{\displaystyle 2}}{\displaystyle n_{\displaystyle 1}}\). (4)

Нетрудно видеть, что сформулированный ранее закон преломления для перехода "воздух–среда" является частным случаем данного закона. В самом деле, полагая в формуле (4) \(n_{\displaystyle 1}=1, n_{\displaystyle 2}=n\), мы придём к формуле (1).

Вспомним теперь, что показатель преломления - это отношение скорости света в вакууме к скорости света в данной среде: \(n_{\displaystyle 1}=c/v_{\displaystyle1}, n_{\displaystyle 2}=c/v_{\displaystyle2}\). Подставляя это в (4), получим:

\(\frac{\displaystyle sin\alpha}{\displaystyle sin\beta }=\frac{\displaystyle v_{\displaystyle 1}}{\displaystyle v_{\displaystyle 2}}\). (5)

Формула (5) естественным образом обобщает формулу (3). Отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде.

Полное внутреннее отражение.

При переходе световых лучей из оптически более плотной среды в оптически менее плотную наблюдается интересное явление - полное внутреннее отражение. Давайте разберёмся, что это такое.

Будем считать для определённости, что свет идёт из воды в воздух. Предположим, что в глубине водоёма находится точечный источник света \(S\), испускающий лучи во все стороны. Мы рассмотрим некоторые из этих лучей (рис. 5).

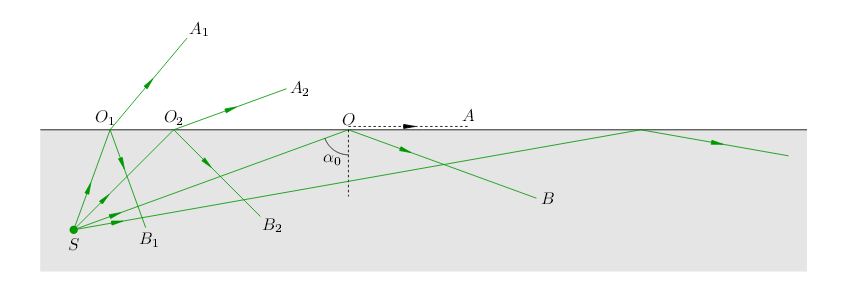Рис. 5. Полное внутреннее отражение

Луч \(SO_{\displaystyle 1}\) падает на поверхность воды под наименьшим углом. Этот луч частично преломляется (луч \(O_{\displaystyle 1} A_{\displaystyle 1}\)) и частично отражается назад в воду (луч \(O_{\displaystyle 1} B_{\displaystyle 1}\)). Таким образом, часть энергии падающего луча передаётся преломлённому лучу, а оставшаяся часть энергии -отражённому лучу.

Угол падения луча \(S O_{\displaystyle 2} \) больше. Этот луч также разделяется на два луча - преломлённый и отражённый. Но энергия исходного луча распределяется между ними по-другому: преломлённый луч \(O_{\displaystyle 2} A_{\displaystyle 2}\) будет тусклее, чем луч \(O_{\displaystyle 1} A_{\displaystyle 1}\) (то есть получит меньшую долю энергии), а отражённый луч \(O_{\displaystyle 2} B_{\displaystyle 2}\) - соответственно ярче, чем луч \(O_{\displaystyle 1} B_{\displaystyle 1}\) (он получит большую долю энергии).

По мере увеличения угла падения прослеживается та же закономерность: всё большая доля энергии падающего луча достаётся отражённому лучу, и всё меньшая - преломлённому лучу. Преломлённый луч становится всё тусклее и тусклее, и в какой-то момент исчезает совсем!

Это исчезновение происходит при достижении угла падения \(\alpha _{0}\), которому отвечает угол преломления \(90^{\circ}\). В данной ситуации преломлённый луч \(OA\) должен был бы пойти параллельно поверхности воды, да идти уже нечему - вся энергия падающего луча \(SO\) целиком досталась отражённому лучу \(OB\).

При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.

Описанное явление и есть полное внутреннее отражение. Вода не выпускает наружу лучи с углами падения, равными или превышающими некоторое значение \(\alpha _{0}\) - все такие лучи целиком отражаются назад в воду. Угол \(\alpha _{0}\) называется предельным углом полного отражения.

Величину \(\alpha _{0}\) легко найти из закона преломления. Имеем:

\(\frac{\displaystyle sin\alpha _{0}}{\displaystyle sin90^{\circ}}=\frac{\displaystyle 1}{\displaystyle n}\).

Но \(sin90^{\circ}=1\), поэтому

\(sin\alpha _{0}=\frac{\displaystyle 1}{\displaystyle n}\),

откуда

\(\alpha _{0}=arcsin\frac{\displaystyle 1}{\displaystyle n}\).

Так, для воды предельный угол полного отражения равен:

\(\alpha _{0}=arcsin\frac{\displaystyle 1}{1,33} \approx 48,8^{\circ} \).

Явление полного внутреннего отражения вы легко можете наблюдать дома. Налейте воду в стакан, поднимите его и смотрите на поверхность воды чуть снизу сквозь стенку стакана. Вы увидите серебристый блеск поверхности - вследствие полного внутреннего отражения она ведёт себя подобно зеркалу.

Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.

Разберем задачи ЕГЭ по теме: Преломление света.

Задача 1. Нижняя грань AC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина \(\alpha = 30^{\circ} \). Луч света падает из воздуха на клин перпендикулярно грани AB, преломляется и выходит в воздух через ту же грань AB, но уэе под углом преломления \(\beta = 90^{\circ}\) Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.

Дано:
\(\alpha = 30^{\circ} \)
\(\beta = 90^{\circ}\)
n-?
Решение. Решение задач по геометрической оптике необходимо начинать с построения чертежа (рисунка), моделирующего условия, описанные в тексте задачи.

Световой луч падает на прозрачный клин перпендикулярно стороне АВ (см.рис.1). В этом случае, световой луч не преломляется на границе раздела воздух-клин, так как угол падения равен 0, соответственно, угол преломления также равен 0. Следовательно, внутри клина световой луч попадает на нижнюю грань АС, которая представляет собой плоское зеркало. Согласно рис.1 величина угла \(\alpha_1=180^{\circ}-(\alpha+90^{\circ})=90^{\circ}-\alpha.\)

\(\alpha_1=90^{\circ}-30^{\circ}=60^{\circ}.\)

Тогда угол падения луча на плоское зеркало будет равен
\(90^{\circ}-\alpha_1=90^{\circ}-60^{\circ}=30^{\circ}.\)

То есть угол падения равен \(\alpha=30^{\circ}\).
Согласно закону отражения света, угол падения светового луча равен углу отражения. В треугольнике МКО угол КОМ образован суммой двух углов α, поэтому он равен 60°. Тогда угол падения светового луча на грань АВ также будет равен \(2\alpha=60^{\circ}\) (равенство накрест лежащих углов).
На следующем этапе задачи надо применить закон преломления света, так как луч переходит из одной среды в другую.
\(\frac{\sin{2\alpha}}{\sin\beta}=\frac{1}{n}\)
При записи этой формулы учтено, что второй средой является воздух с показателем преломления равным 1, а первой средой является материал клина с показателем преломления n, который необходимо определить. Из последней формулы можно выразить и рассчитать n.

\(n=\frac{\sin\beta}{\sin2\alpha}\)

\(n=\frac{\sin90^{\circ}}{\sin(2\cdot 30^{\circ})}=\frac{\sin90^{\circ}}{\sin60^{\circ}}\approx 1,15\)

Ответ: 1,15

Задача 2. На тонкую собирающую линзу от удалённого источника падает пучок параллельных лучей (см. рисунок). Как изменится положение изображения источника, создаваемого линзой, если между линзой и её фокусом поставить
плоскопараллельную стеклянную пластинку с показателем преломления n (на рисунке положение пластинки отмечено пунктиром)? Ответ поясните, указав, какие физические закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной стеклянной пластинки.

Решение. Рассмотрим ход световых лучей от удаленного источника через линзу при отсутствии плоскопараллельной стеклянной пластинки (см.рис.1).

Луч 1-1ʹ проходит через оптический центр линзы и не преломляется. Луч 2-2ʹ идет через фокус и после прохождения через линзу, идет параллельно главной оптической оси. Пересечение этих двух лучей дает действительное изображение удаленного источника, которое расположено в фокальной плоскости линзы. Этот факт также можно доказать, используя формулу тонкой линзы.

\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F} (1)\)

Так как источник света расположен на расстоянии \(d \rightarrow \infty,\) то \(\frac{1}{d}\rightarrow 0.\)

Тогда формула тонкой линзы (1) примет вид \(\frac{1}{f}=\frac{1}{F},\) следовательно, f=F, т.е. изображение формируется в фокальной плоскости линзы.

Рассмотрим ход световых лучей через плоскопараллельную стеклянную пластинку. Для этого необходимо использовать закон преломления света.

Рис.2

Согласно рис.2 угол падения луча на пластину равен α. Закон преломления света на границе раздела воздух-пластинка имеет вид:

\(\frac{\sin\alpha}{\sin\beta}=\frac{n}{1}=n (1).\)

Здесь учтено, что показатель преломления воздуха равен 1, а пластинки n.
При переходе светового луча из пластинки в воздух, закон преломления света будет иметь вид:

\(\frac{\sin\beta}{\sin\gamma}=\frac{1}{n} (2).\)

В этом случае первой средой является пластинка с показателем преломления n, а второй средой будет воздух с показателем преломления равным 1.
Из (1) и (2) выразим \(\sin\alpha\) и \(\sin\gamma\).

\(\sin\alpha=n\sin\beta\) и \(\sin\gamma=n\sin\beta.\)

Так как правые части этих уравнений равны, то \(\sin\alpha=\sin\gamma.\)

Отсюда вытекает равенство углов \(\alpha=\gamma\). Следовательно, луч, падающий на стеклянную пластину, выходит из нее, оставаясь параллельным входящему лучу. Но при этом выходящий луч немного смещается вверх.

Исходя из этого можно сделать вывод, что изображение удаленного источника после прохождения через плоскопараллельную стеклянную пластину, не изменится. Из удаленного источника выходит бесконечное количество параллельных лучей, которые собираются в фокальной плоскости линзы.

Ответ: не изменится.

Задача 3. Ученик провел опыт по преломлению света, представленный на фотографии. Как изменится при уменьшении угла падения угол преломления светового пучка и скорость света, распространяющегося в стекле? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшиться
3) не изменится
Запишите в таблицу выбранные цифры для каждой величины. Цифры в ответе могут повторяться.

Решение. Для ответа на первый вопрос задачи необходимо применить закон преломления света для границы раздела воздух-стекло.

\(\frac{\sin\alpha}{\sin\beta}=\frac{n}{1}=n.\)

Показатель преломления стекла равен n, а воздуха 1.
При уменьшении угла падения α, будет уменьшаться и значение \(\sin\alpha.\) Так как показатель преломления стекла не изменяется, то значение \(\sin\beta\) так же будет уменьшаться. Поэтому угол преломления уменьшится.

Для ответа на второй вопрос надо учесть, что скорость света в данной среде определяется значением показателя преломления \(v_{cp}=\frac{c}{n},\) где с – скорость света в вакууме, а n – показатель преломления среды (стекла). Так как эти обе величины не изменяются, то скорость света в стекле так же не изменяется.

Ответ: 23.

Задача 4. Чему равен синус предельного угла полного внутреннего отражения при переходе света из вещества с \(n_1=1,5\) в вещество с \(n_2=1,2\)?

Решение.

Явление полного внутреннего отражения наблюдается при переходе светового луча из оптически более плотной среды в оптически менее плотную (см.рис.1). Источник света S должен находиться в среде с большим показателем преломления.

Для нахождения синуса угла полного внутреннего отражения необходимо воспользоваться законом преломления света.

\(\frac{\sin\alpha_{np}}{\sin\beta}=\frac{n_2}{n_1} (1)\)

При полном внутреннем отражении преломленный луч скользит по границе раздела двух сред и угол преломления \(\beta=90^{\circ}\). С учетом того, что \(\sin90^{\circ}=1\) уравнение (1) примет вид:

\(\sin\alpha_{np}=\frac{1,2}{1,5}=0,8\)

\(\sin\alpha_{np}=0,8\)

Ответ: 0,8.

Если вам нравятся наши материалы - записывайтесь на курсы подготовки к ЕГЭ по физике онлайн