Принципы СТО.

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: принцип относительности Эйнштейна, инвариантность скорости света.

Принцип относительности Галилея, подробно рассмотренный в предыдущем листке, говорит о том, что никакие лабораторные опыты механики не помогут определить, покоится ли лаборатория или движется равномерно и прямолинейно.

Но возникает закономерный вопрос: а кто заставляет нас ограничиваться лишь механическими явлениями? Давайте перейдём в другие области физики: будем наблюдать в движущейся лаборатории распространение тепла или света, ставить опыты с электромагнитными колебаниями, изучать ядерные процессы. . . Раз уж механика нам не помощник, то, быть может, где-нибудь в молекулярной физике, электродинамике, оптике, атомной или ядерной физике найдутся явления, на протекании которых скажется равномерно-прямолинейное движение лаборатории? Тогда, сопоставив ход таких явлений в неподвижной и в движущейся системах отсчёта, мы зафиксируем факт движения и сможем измерить его скорость.

С развитием электродинамики поначалу казалось, что так оно и есть. Дело в том, что, в отличие от законов механики Ньютона, уравнения Максвелла оказались не инвариантными относительно преобразований Галилея.

Гипотеза о мировом эфире.

 

Из уравнений Максвелла следует, например, что свет в вакууме распространяется со скоростью c= 300000 км/с в любом направлении, причём эта скорость не зависит от того, покоится ли источник света или движется. Физиков данный факт ничуть не удивлял: свет рассматривался как колебания особой всепроникающей среды - неподвижного мирового эфира. Считалось, что электромагнитные волны распространяются в эфире аналогично звуковым волнам в воздухе, а со звуком ведь дело обстоит точно так же: сигнал от бибикнувшего автомобиля бежит в воздухе во все стороны со скоростью примерно 330 м/с вне зависимости от скорости, с которой движется автомобиль.

А теперь представьте себе, что вы находитесь в звездолёте, который мчится в космическом вакууме со скоростью v= 50000км/с относительно удалённых звёзд. Вы сидите лицом по ходу движения звездолёта и смотрите на лампочку, которая находится в его носовой части.

Свет от лампочки, не обращая внимания на её движение, перемещается относительно звёзд со скоростью c. Вы движетесь навстречу свету со скоростью v; стало быть, относительно вас свет имеет скорость
c+v= 350000 км/с. Вы измеряете эту скорость, сопоставляете её с известным значением c и приходите к выводу, что двигаетесь со скоростью 50000 км/с! Таким образом, электромагнитные явления вроде бы позволяют отличить покой от равномерного прямолинейного движения.

У вас, кстати, может возникнуть вопрос: а чем плох аналогичный эксперимент со звуком? Давайте бибикнем в носовой части длинного движущегося лимузина, измерим скорость звука относительно нас и опровергнем принцип относительности Галилея! Ничего не выйдет: если лимузин замкнутый (как и должно быть), то он увлекает свой воздух вместе с собой, и вы ничего не заметите. А вот в звездолёте вам никуда не деться от всепроникающего "эфирного ветра", который несётся вам в лицо и увеличивает тем самым скорость света в описанном выше эксперименте с лампочкой. (Пытаясь спасти принцип относительности Галилея применительно к электродинамике, Герц предположил, что эфир также увлекается движущимися телами. Из этой гипотезы следовало, однако, что струя воды, увлекая эфир, должна увлекать и луч света - а в экспериментах такого не наблюдалось.)

Соответственно, многие учёные (в том числе выдающийся голландский физик Х. Лоренц) считали, что инерциальные системы отсчёта, будучи равноправными с точки зрения механики, в электродинамике перестают быть таковыми. Имеется выделенная, привилегированная система отсчёта, связанная с неподвижным мировым эфиром. Остальные системы отсчёта движутся относительно неё, и возникающий "эфирный ветер" меняет в них величину скорости света.

С целью обнаружения эфирного ветра в 1881 году был поставлен один из самых знаменитых физических экспериментов - опыт Майкельсона. С помощью чувствительного интерферометра производились попытки измерить скорость Земли относительно эфира. А именно, исследовалась интерференционная картина, даваемая двумя когерентными пучками света, имеющими перпендикулярные направления. Интерферометр движется относительно эфира вместе с Землёй; при вращении интерферометра меняется направление эфирного ветра относительно интерферометра, что должно сказываться на скоростях пучков и давать сдвиги интерференционной картины.

Однако никаких сдвигов обнаружено не было! Наблюдения проводились в разное время года (когда скорость Земли ощутимо меняла направление) и неизменно давали отрицательный результат. Интерферометр был настолько точный, что списать отсутствие эфирного ветра на недостаточную чувствительность прибора было нельзя.

Почему же движение Земли относительно эфира не удаётся зафиксировать? Не сомневаясь в существовании эфира, Лоренц заметил, что результаты опыта Майкельсона полностью объясняются, если сделать невероятное предположение: размеры движущегося предмета сокращаются в направлении движения! Так, если стержень длины \(l_{0}\) начинает двигаться вдоль своей оси со скоростью \(v\), то его длина становится равной:

\(l=l_{\displaystyle 0}\sqrt{\displaystyle 1-\frac{\displaystyle v^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}\) (1)Эта гипотеза, названная лоренцевым сокращением, не вытекала на тот момент из каких-либо физических принципов и стояла особняком, будучи призвана лишь справиться с отрицательным результатом опыта. Но тем не менее формула (1) действительно оказалась верна! Её объяснение пришло позже, уже в рамках теории относительности Эйнштейна.

Постулаты Эйнштейна.

 

Альберт Эйнштейн - величайшая фигура в истории физики. Для разрешения трудностей, описанных выше, он отказался от некоторых сложившихся в физике устоев и предпринял весьма радикальные шаги. Сформулируем ещё раз те проблемы, с которыми столкнулась физика, и их решения, предложенные Эйнштейном.

1. Не удаётся обнаружить привилегированную систему отсчёта, связанную с неподвижным мировым эфиром.

Так её и нет вовсе. Никакого эфира не существует. Все инерциальные системы отсчёта полностью равноправны между собой, и никакими физическими опытами нельзя выделить одну из них среди остальных.

Таким образом, Эйнштейн обобщил принцип относительности Галилея с механических на вообще все физические явления.

Принцип относительности Эйнштейна. Всякое физическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта.

Следовательно, если ваша лаборатория находится внутри корабля, то не только механический, но и вообще никакой эксперимент не даст вам ответа на вопрос, покоится ли корабль или движется равномерно и прямолинейно. Вы можете ставить опыты с газами, изучать тепловые явления, наблюдать за распространением электромагнитных волн, следить за атомными и ядерными процессами, анализировать взаимодействия элементарных частиц - и нигде вам не удастся обнаружить каких-либо отклонений в протекании этих явлений, вызванных фактом равномерно-прямолинейного движения корабля.

В предыдущем разделе мы убедились в том, что законы механики имеют одинаковую математическую форму во всех инерциальных системах отсчёта: уравнения, выражающие эти законы, инвариантны относительно преобразований Галилея. Таков смысл принципа относительности Галилея. Обобщающий его принцип относительности Эйнштейна утверждает, что любой физический закон имеет одинаковую математическую форму во всех инерциальных системах отсчёта. Все уравнения, выражающие законы физики, должны быть инвариантны относительно перехода из одной инерциальной системы отсчёта в другую.

В частности, основные уравнения электродинамики - уравнения Максвелла - должны сохранять свою форму при таком переходе. Как же тогда быть со следующей трудностью?

2. Электродинамика противоречит механике в том, что уравнения Максвелла не инвариант-\ны относительно преобразований Галилея.

Что ж, это проблема механики, а не электродинамики. Уравнения Максвелла блестяще работают в области электромагнитных явлений. Если преобразования Галилея не вяжутся с уравнениями Максвелла, то неверны преобразования Галилея, а не уравнения Максвелла.

Но легко сказать - преобразования Галилея неверны! Во-первых, они, казалось бы, совершенно очевидны - вам наверняка не составило труда в них разобраться. Чему там, собственно говоря, быть неверным?

А во-вторых - следствием преобразований Галилея, как мы видели, является закон сложения скоростей. Вы неоднократно пользовались им при решении задач. Что же получается - и закон сложения скоростей объявляется неверным?

Да, именно так - гласил ответ Эйнштейна. Классическая механика Ньютона нуждается в глубоком, коренном пересмотре своих основных принципов. И слабый пункт классической механики состоит в том, что механические законы предполагают мгновенность распространения взаимодействий между телами.

Рассмотрим, например, гравитационное притяжение двух тел. Если одно из тел сместить в сторону, то, согласно закону всемирного тяготения, второе тело "почувствует" этот факт мгновенно, как только изменится расстояние от него до первого тела. Получается, что взаимодействие передаётся от одного тела к другому с бесконечной скоростью.

Эксперименты, однако, показывают, что механизм передачи взаимодействий состоит в следующем: изменение состояния тела меняет поле около него; возникшее возмущение поля начинает бежать во все стороны с некоторой конечной скоростью и лишь спустя определённый промежуток времени достигает другого тела. Мгновенно передающихся взаимодействий ни в каких опытах не наблюдается.

Но если взаимодействия не могут передаваться в бесконечной скоростью, то в природе существует предельная, максимальная скорость распространения взаимодействий. Изменённые законы механики должны учитывать наличие этой предельной скорости и, соответственно, конечность времени передачи взаимодействий между телами.

Второй постулат Эйнштейна отводит исключительную роль скорости света.

Принцип инвариантности скорости света. В каждой инерциальной системе отсчёта свет движется в вакууме с одной и той же скоростью; величина этой скорости не зависит от того, покоится или движется источник света.

Таким образом, вышеописанный опыт с лампочкой в носовой части звездолёта нам провести не удастся: скорость света относительно наблюдателя в звездолёте будет равна c, а не c+v, и наблюдатель не может заметить факт движения звездолёта. Классический закон сложения скоростей применительно к скорости света не работает.

Мы увидим далее, что максимальная скорость распространения взаимодействий, присущая нашему миру, оказывается равной как раз скорости света в вакууме. Никакой сигнал, никакое тело, никакой вообще материальный объект в природе не может двигаться со скоростью, превышающей c. Величина c является фундаментальной константой, отражающей свойства мира, в котором мы живём.

Оба постулата Эйнштейна - принцип относительности и принцип инвариантности скорости света - легли в основу специальной теории относительности (СТО). Эта теория затрагивает глубокие свойства пространства-времени, радикально меняя наши представления об окружающем мире. Механика, построенная Эйнштейном на постулатах СТО, получила название релятивистской (от англ. relativity - относительность).

Новые и удивительные свойства пространства-времени и новые законы, устанавливаемые в СТО, проявляются при больших скоростях движения - и тем ярче, чем ближе мы подходим к скорости света. В повседневной жизни мы не замечаем этих релятивистских эффектов - по той простой причине, что привычные нам скорости чрезвычайно малы по сравнению со скоростью света. Во многих практических задачах можно считать скорость света бесконечной - и тогда прекрасно работает классическая механика.

Итак, классическая механика оказывается приближённой теорией и годится для небольших скоростей. Релятивистская механика используется тогда, когда скорости тел достаточно близки к скорости света - в таких ситуациях классическая механика отказывает совершенно. Классическая механика является предельным случаем релятивистской механики: формулы классической механики получаются из релятивистских формул предельным переходом \(c\rightarrow \infty \).

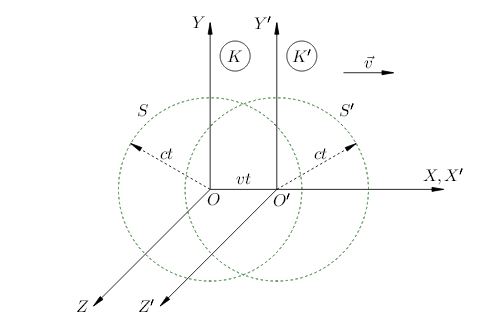Рис. 1. Кажущийся парадокс со световой вспышкой

 

Какие же новые свойства пространства-времени и новые физические законы открыла теория относительности? Мы будем рассказывать о них в двух следующих разделах. Здесь мы покажем лишь, что из постулатов СТО следуют весьма неожиданные и, казалось бы, парадоксальные выводы.

Рассмотрим системы отсчёта \(K\) и \(K{}'\) - те же, что и в предыдущей теме (рис. 1). В момент времени \(t=0\), когда их начала \(O\) и \(O{}'\)находятся в одной точке, в этой точке происходит световая вспышка.

Где окажется волновой фронт вспышки к моменту времени \(t\)?

В системе \(K\) свет распространяется во все стороны со скоростью \(c\). Поэтому в системе \(K\) вспышка достигнет сферы \(S\) радиуса \(ct\) с центром в точке \(O\).

В системе \(K{}'\) скорость света также равна \(c\). Значит, в системе \(K{}'\) вспышка достигнет сферы \(S{}'\) того же радиуса \(ct\), но с центром в точке \(O{}'\).

Однако точки \(O\) и \(O{}'\) к моменту \(t\) разойдутся на расстояние \(vt\). Получается, что волновой фронт в один и тот же момент времени находится на двух разных сферах \(S\) и \(S{}'\). Противоречие?

Противоречия на самом деле нет. Причина кажущегося парадокса кроется в понятии одновременности. На место нашего интуитивного понимания одновременности приходит чёткое определение этого термина, даваемое в СТО.