Релятивистская динамика

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: полная энергия, связь массы и энергии, энергия покоя.

В классической динамике мы начали с законов Ньютона, потом перешли к импульсу, а после него — к энергии. Здесь мы ради простоты изложения поступим ровно наоборот: начнём с энергии, затем перейдём к импульсу и закончим релятивистским уравнением движения — модификацией второго закона Ньютона для теории относительности.

Релятивистская энергия

Предположим, что изолированное тело массы \(m\) покоится в данной системе отсчёта. Одно из самых впечатляющих достижений теории относительности — это знаменитая формула Эйнштейна:

\(E=mc^{2}\) (1)

Здесь \(E\) — энергия тела, \(c\) — скорость света в вакууме. Поскольку тело покоится, энергия \(E\), вычиляемая по формуле (1), называется энергией покоя.

Формула (1) утверждает, что каждое тело само по себе обладает энергией — просто потому, что оно существует в природе. Образно говоря, природа затратила определённые усилия на то, чтобы «собрать» данное тело из мельчайших частиц вещества, и мерой этих усилий служит энергия покоя тела. Энергия эта весьма велика; так, в одном килограмме вещества заключена энергия

\(E=1\cdot (3\cdot 10^{8})^{2}=9\cdot 10^{16}\) Дж.

Интересно, какое количество топлива нужно сжечь, чтобы выделилось столько энергии? Возьмём, например, дерево. Его удельная теплота сгорания равна \(q=10^{7}\) Дж/кг, поэтому находим: \(m= E/q= 9\cdot 10^{9}\) кг. Это девять миллионов тонн!

Ещё для сравнения: такую энергию единая энергосистема России вырабатывает примерно за десять дней.

Почему столь грандиозная энергия, содержащаяся в теле, до сих пор оставалась нами незамеченной? Почему в нерелятивистских задачах, связанных с сохранением и превращением энергии, мы не учитывали энергию покоя? Скоро мы ответим на этот вопрос.

Поскольку энергия покоя тела прямо пропорциональна его массе, изменение энергии покоя на величину \(\Delta E\) приводит к изменению массы тела на

\(\Delta m= \frac{\Delta \displaystyle E}{\displaystyle c^{\displaystyle 2}}\).

Так, при нагревании тела возрастает его внутренняя энергия, и, стало быть, масса тела увеличивается! В повседневной жизни мы не замечаем этого эффекта ввиду его чрезвычайной малости. Например, для нагревания воды массой \(m= 1\) кг на \(\Delta t= 100^{\circ}C\) (удельная теплоёмкость воды равна \(c_{b}= 4200 J/(kg\cdot^{\circ}C)\)) ей нужно передать количество теплоты:

\(Q= c_{b}m\Delta t= 4,2\cdot 10^{5}\) Дж.

Увеличение массы воды будет равно:

\(\Delta m= \frac{Q}{c^{2}}= \frac{4,2\cdot 10^{5}}{9\cdot 10^{16}}\approx 4,7\cdot 10^{-12}\) кг.

Столь ничтожное изменение массы невозможно заметить на фоне погрешностей измерительных приборов.

Формула ( 1) даёт энергию покоящегося тела. Что изменится, если тело движется?

Снова рассмотрим неподвижную систему отсчёта \(K\) и систему \({K}'\), движущуюся относительно \(K\) со скоростью \(\upsilon\). Пусть тело массы \(m\) покоится в системе \({K}'\); тогда энергия тела в системе \({K}'\) есть энергия покоя, вычисляемая по формуле ( 1). Оказывается, при переходе в систему \(K\) энергия преобразуется так же, как и время — а именно, энергия тела в системе \(K\), в которой тело движется со скоростью \(\upsilon \), равна:

\(E= \frac{mc^{2}}{\sqrt{\displaystyle 1-\frac{\upsilon ^{\displaystyle 2}}{c^{\displaystyle 2}}}}\) ( 2)

Формула ( 2) была также установлена Эйнштейном. Величина \(E\) — это полная энергия движущегося тела. Поскольку в данной формуле \(mc^{2}\) делится на «релятивистский корень», меньший единицы, полная энергия движущегося тела превышает энергию покоя. Полная энергия будет равна энергии покоя только при \(\upsilon = 0\).

Выражение для полной энергии ( 2) позволяет сделать важные выводы о возможных скоростях движения объектов в природе.

1. Каждое массивное тело обладает определённой энергией, поэтому необходимо выполнение неравенства

\(1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}\) > \(0\).

Оно означает, что \(\upsilon\) < \(c\): скорость массивного тела всегда меньше скорости света.

2. В природе существуют безмассовые частицы (например, фотоны), несущие энергию. При подстановке \(m= 0\) в формулу ( 2) её числитель обращается в нуль. Но энергия-то фотона ненулевая!

Единственный способ избежать здесь противоречия — это принять, что безмассовая частица обязана двигаться со скоростью света. Тогда и знаменатель нашей формулы обратится в нуль, так что формула ( 2) попросту откажет. Нахождение формул для энергии безмассовых частиц не входит в компетенцию теории относительности. Так, выражение для энергии фотона устанавливается в квантовой физике.

Интуитивно чувствуется, что полная энергия ( 2) состоит из энергии покоя и собственно «энергии движения», т. е. кинетической энергии тела. При малых скоростях движения это показывается явным образом. Используем приближённые формулы, справедливые при \(\alpha \ll 1\):

\(\sqrt{1-\alpha }\approx 1-\frac{\alpha }{2}\) ( 3)
\(\frac{1}{1-\alpha }\approx 1+\alpha \) ( 4)

С помощью этих формул последовательно получаем из ( 2):

\(E= \frac{\displaystyle mc^{\displaystyle 2}}{\sqrt{\displaystyle 1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}\approx \frac{\displaystyle mc^{\displaystyle 2}}{1-\frac{\displaystyle 1}{\displaystyle 2}\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}\approx mc^{2}(1+\frac{\displaystyle 1}{\displaystyle 2}\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}})= mc^{2}+\frac{\displaystyle m\upsilon ^{\displaystyle 2}}{\displaystyle 2}\) ( 5)

Таким образом, при малых скоростях движения полная энергия сводится просто к сумме энергия покоя и кинетической энергии. Это служит мотивировкой для определения понятия кинетической энергии в теории относительности:

\(E_{K}=\frac{mc^{2}}{\sqrt{1-\frac{\upsilon ^{2}}{c^{2}}}}-mc^{2}\). ( 6)

При \(\upsilon \ll c\) формула ( 6) переходит в нерелятивистское выражение \(E_{K}= m\upsilon ^{2}/2\).

Теперь мы можем ответить на заданный выше вопрос о том, почему до сих пор не учитывалась энергия покоя в нерелятивистских энергетических соотношениях. Как видно из ( 5), при малых скоростях движения энергия покоя входит в полную энергию в качестве слагаемого. В задачах, например, механики и термодинамики изменения энергии тел составляют максимум несколько миллионов джоулей; эти изменения столь незначительны по сравнению с энергиями покоя рассматриваемых тел, что приводят к микроскопическим изменениям их масс. Поэтому с высокой точностью можно считать, что суммарная масса тел не меняется в ходе механических или тепловых процессов. В результате суммы энергий покоя тел в начале и в конце процесса попросту сокращаются в обеих частях закона сохранения энергии!

Но такое бывает не всегда. В других физических ситуациях изменения энергии тел могут приводить к более заметным изменениям суммарной массы. Мы увидим, например, что в ядерных реакциях отличия масс исходных и конечных продуктов обычно составляют доли процента.Скажем, при распаде ядра урана \(_{92}^{235}{\cup }\) суммарная масса продуктов распада примерно на \(0,1\%\) меньше массы исходного ядра. Эта одна тысячная доля массы ядра высвобождается в виде энергии, которая при взрыве атомной бомбы способна уничтожить город.

При неупругом столкновении часть кинетической энергии тел переходит в их внутренюю энергию. Релятивистский закон сохранения полной энергии учитывает этот факт: суммарная масса тел после столкновения увеличивается!

Рассмотрим в качестве примера два тела массы \(m\), летящих навстречу друг другу с одинаковой скоростью \(3c/5\). В результате неупругого столкновения образуется тело массы \(M\) , скорость которого равна нулю по закону сохранения импульса (об этом законе речь впереди). Согласно закону сохранения энергии получаем:

\(\frac{\displaystyle mc^{\displaystyle 2}}{\sqrt{\displaystyle 1-\frac{(\displaystyle 3c/5)^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}+\frac{\displaystyle mc^{\displaystyle 2}}{\sqrt{\displaystyle 1-\frac{(\displaystyle 3c/5)^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}= Mc^{2}\),

\(2\cdot \frac{\displaystyle mc^{\displaystyle 2}}{\sqrt{\displaystyle 1-(\frac{\displaystyle 3}{\displaystyle 5})^{\displaystyle 2}}}= Mc^{2}\),

\(\frac{\displaystyle 2m}{\displaystyle 4/5}= M\),

\(M= \frac{\displaystyle 5}{\displaystyle 2}m\).

Мы видим, что, \(M\) > \(2m\) — масса образовавшегося тела превышает сумму масс тел до столкновения. Избыток массы, равный \(m/2\), возник за счёт перехода кинетической энергии сталкивающихся тел во внутреннюю энергию.

Релятивистский импульс.

Классическое выражение для импульса \(\vec{p}= m\vec{\upsilon }\) не годится в теории относительности — оно, в частности, не согласуется с релятивистским законом сложения скоростей. Давайте убедимся в этом на следующем простом примере.

Пусть система \({K}'\) движется относительно системы \(K\) со скоростью \(v = c/2\) (рис. 1). Два тела массы \(m\) в системе \({K}'\) летят навстречу друг другу с одинаковой скоростью \({u}'= c/2\). Происходит неупругое столкновение.

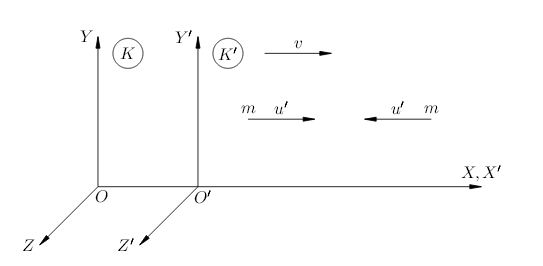Рис. 1. К закону сохранения импульса

В системе \({K}'\) тела после столкновения останавливаются. Давайте, как и выше, найдём массу \(M\) образовавшегося тела:

\(Mc^{2}= 2\frac{\displaystyle mc^{\displaystyle 2}}{\sqrt{\displaystyle 1-\frac{(\displaystyle c/2)^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}= \frac{\displaystyle 2mc^{\displaystyle 2}}{\sqrt{\displaystyle 1-(\frac{\displaystyle 1}{\displaystyle 4})^{\displaystyle 2}}}= \frac{\displaystyle 4mc^{\displaystyle 2}}{\sqrt{\displaystyle 3}}\),

откуда

\(M= \frac{\displaystyle 4m}{\sqrt{\displaystyle 3}}\).

Теперь посмотрим на процесс столкновения с точки зрения системы \(K\). До столкновения левое тело имеет скорость:

\(u_{1}= \frac{\displaystyle \upsilon +{\displaystyle u}'}{\displaystyle 1+\frac{\displaystyle \upsilon {\displaystyle u}'}{\displaystyle c^{\displaystyle 2}}}= \frac{\displaystyle c/2+\displaystyle c/2}{\displaystyle 1+\frac{(\displaystyle c/2)(\displaystyle c/2)}{\displaystyle c^{\displaystyle 2}}}= \frac{\displaystyle 4c}{\displaystyle 5}\).

Правое тело имеет скорость:

\(u_{2}= \frac{\displaystyle \upsilon -{\displaystyle u}'}{1-\frac{\displaystyle \upsilon {\displaystyle u}'}{\displaystyle c^{\displaystyle 2}}}= \frac{\displaystyle c/2-\displaystyle c/2}{1-\frac{(\displaystyle c/2)(\displaystyle c/2)}{\displaystyle c^{\displaystyle 2}}}= 0\).

Нерелятивистский импульс нашей системы до столкновения равен:

\(mu_{1}-mu_{2}= \frac{\displaystyle 4mc}{\displaystyle 5}\).

После столкновения получившееся тело массы \(M\) двигается со скоростью \(\upsilon = c/2\).
Его нерелятивистский импульс равен:

\(M\upsilon = \frac{\displaystyle 4m}{\sqrt{\displaystyle 3}}\frac{\displaystyle c}{\displaystyle 2}= \frac{\displaystyle 2m}{\sqrt{\displaystyle 3}}\).

Как видим, \(mu_{1}-mu_{2}\neq M\upsilon \), то есть нерелятивистский импульс не сохраняется.

Оказывается, правильное выражение для импульса в теории относительности получается делением классического выражения на «релятивистский корень»: импульс тела массы \(m\), двигающегося со скоростью \(\vec{\upsilon }\), равен:

\(\vec{p}= \frac{\displaystyle m\vec{\displaystyle \upsilon }}{\sqrt{\displaystyle 1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}\). 7

Давайте вернёмся к только что рассмотренному примеру и убедимся, что теперь с законом сохранения импульса всё будет в порядке.

Импульс системы до столкновения:

\(p_{before}= \frac{\displaystyle mu_{\displaystyle 1}}{\sqrt{\displaystyle 1-\frac{\displaystyle u_{\displaystyle 1}^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}- \frac{\displaystyle mu_{\displaystyle 2}}{\sqrt{\displaystyle 1-\frac{\displaystyle u_{\displaystyle 2}^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}= \frac{\displaystyle m(\displaystyle 4c/5)}{\displaystyle \sqrt{\displaystyle 1-\frac{(\displaystyle 4c/5)^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}-0= \frac{\displaystyle 4mc/5}{\displaystyle 3/5}= \frac{\displaystyle 4mc}{\displaystyle 3}\).

Импульс после столкновения:

\(p_{after}= \frac{\displaystyle \displaystyle M\upsilon }{\sqrt{\displaystyle 1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}= \frac{\displaystyle Mc/2}{\sqrt{\displaystyle 1-\frac{(\displaystyle c/2)^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}=( \frac{\displaystyle 4m/\sqrt{\displaystyle 3})(\displaystyle c/2)}{\sqrt{\displaystyle 3/2}}= \frac{\displaystyle 4mc}{\displaystyle 3}\)

Вот теперь всё правильно: \(p_{before}= p_{after}\)!

Связь энергии и импульса.

Из формул ( 2) и ( 7) можно получить замечательное соотношение между энергией и импульсом в теории относительности. Возводим обе части этих формул в квадрат:

\(E^{2}= \frac{\displaystyle m^{\displaystyle 2}c^{\displaystyle 4}}{1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}\), \(p^{2}= \frac{\displaystyle m^{\displaystyle 2}\upsilon ^{\displaystyle 2}}{\displaystyle 1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}\)

Преобразуем разность:

\(E^{2}-p^{2}c^{2}= \frac{\displaystyle m^{\displaystyle 2}\displaystyle c^{\displaystyle 4}}{1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}-\frac{\displaystyle m^{\displaystyle 2}\upsilon ^{\displaystyle 2}c^{\displaystyle 2}}{1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}= \frac{\displaystyle m^{\displaystyle 2}\displaystyle c^{\displaystyle 2}(\displaystyle c^{\displaystyle 2}-\displaystyle \upsilon ^{\displaystyle 2})}{\frac{\displaystyle c^{\displaystyle 2}-\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}= m^{2}c^{4}\)

Это и есть искомое соотношение:

\(E^{2}-p^{2}c^{2}= m^{2}c^{4}\). ( 8)

Данная формула позволяет выявить простую связь между энергией и импульсом фотона. Фотон имеет нулевую массу и движется со скоростью света. Как уже было замечено выше, сами по себе энергия и импульс фотона в СТО найдены быть не могут: при подстановке в формулы ( 2) и ( 7) значений \(m=0\) и \(\upsilon = c\) мы получим нули в числителе и знаменателе. Но зато с помощью ( 8) легко находим: \(E^{2}-p^{2}c^{2}= 0\), или

\(E= pc\) ( 9)

В квантовой физике устанавливается выражение для энергии фотона, после чего с помощью формулы ( 9) находится его импульс.

Релятивистское уравнение движения.

Рассмотрим тело массы \(m\), движущееся вдоль оси \(X\) под действием силы \(F\). Уравнение движения тела в классической механике — это второй закон Ньютона: \(ma= F\). Если за бесконечно малое время \(dt\) приращение скорости тела равно \(d\upsilon \), то \(a=d\upsilon /dt\), и уравнение движения запишется в виде:

\(m\frac{\displaystyle d\upsilon }{\displaystyle dt}= F\). ( 10)

Теперь заметим, что \(md\upsilon = d(m\upsilon )= dp\) — изменение нерелятивистского импульса тела. В результате получим «импульсную» форму записи второго закона Ньютона — производная импульса тела по времени равна силе, приложенной к телу:

\(\frac{dp}{dt}= F\). ( 11)

Все эти вещи вам знакомы, но повторить никогда не помешает ;-)

Классическое уравнение движения — второй закон Ньютона — является инвариантным относительно преобразований Галилея, которые в классической механике описывают переход из одной инерциальной системы отсчёта в другую (это означает, напомним, что при указанном переходе второй закон Ньютона сохраняет свой вид). Однако в СТО переход между инерциальными системами отсчёта описывается преобразованиями Лоренца, а относительно них второй закон Ньютона уже не является инвариантным. Следовательно, классическое уравнение движения должно быть заменено релятивистским, которое сохраняет свой вид под действием преобразований Лоренца.

То, что второй закон Ньютона ( 10) не может быть верным в СТО, хорошо видно на следующем простом примере. Допустим, что к телу приложена постоянная сила. Тогда согласно классической механике тело будет двигаться с постоянным ускорением; скорость тела будет линейно возрастать и с течением времени превысит скорость света. Но мы знаем, что на самом
деле это невозможно.

Правильное уравнение движения в теории относительности оказывается совсем не сложным.
Релятивистское уравнение движения имеет вид ( 11), где p — релятивистский импульс:

\(\frac{\displaystyle d(\frac{\displaystyle m\upsilon }{\sqrt{\displaystyle 1-\upsilon ^{\displaystyle 2}/\displaystyle c^{\displaystyle 2}}})}{\displaystyle dt}= F\). ( 12)

Производная релятивистского импульса по времени равна силе, приложенной к телу.

В теории относительности уравнение ( 12) приходит на смену второму закону Ньютона.

Давайте выясним, как же в действительности будет двигаться тело массы m под действием постоянной силы \(F\). При условии \(F= const\) из формулы ( 12) получаем:

\(\frac{\displaystyle m\upsilon }{\displaystyle \sqrt{\displaystyle 1-\frac{\displaystyle \upsilon ^{\displaystyle 2}}{\displaystyle c^{\displaystyle 2}}}}= Ft\).

Остаётся выразить отсюда скорость:

\(\upsilon = \frac{\displaystyle cFt}{\sqrt{\displaystyle F^{\displaystyle 2}t^{\displaystyle 2}+m^{\displaystyle 2}c^{\displaystyle 2}}}\). ( 13)

Посмотрим, что даёт эта формула при малых и при больших временах движения.
Пользуемся приближёнными соотношениями при \(\alpha \ll 1\):

\(\sqrt{\displaystyle 1+\alpha }\approx 1+\frac{\displaystyle \alpha }{\displaystyle 2}\), ( 14)

\(\frac{\displaystyle 1}{\displaystyle 1+\alpha }\approx 1-\alpha \). ( 15)

Формулы ( 14) и ( 15) отличаются от формул ( 3) и ( 4) только лишь знаком в левых частях. Очень рекомендую вам запомнить все эти четыре приближённых равенства — они часто используются в физике.

Итак, начинаем с малых времён движения. Преобразуем выражение ( 13) следующим образом:

\(\upsilon = \frac{\displaystyle cFt}{\displaystyle mc\sqrt{\displaystyle 1+\frac{\displaystyle F^{\displaystyle 2}t^{\displaystyle 2}}{\displaystyle m^{\displaystyle 2}c^{\displaystyle 2}}}}\).

При малых \(t\) имеем:

\(\frac{\displaystyle F^{\displaystyle 2}\displaystyle t^{\displaystyle 2}}{\displaystyle m^{\displaystyle 2}\displaystyle c^{\displaystyle 2}}\ll 1\).

Последовательно пользуясь нашими приближёнными формулами, получим:

\(\upsilon \approx \frac{\displaystyle cFt}{\displaystyle mc(1+\frac{\displaystyle 1}{\displaystyle 2}\frac{\displaystyle F^{\displaystyle 2}\displaystyle t^{\displaystyle 2}}{\displaystyle m^{\displaystyle 2}\displaystyle c^{\displaystyle 2}})}\approx \frac{\displaystyle Ft}{\displaystyle m}(1-\frac{F^{\displaystyle 2}t^{\displaystyle 2}}{\displaystyle 2m^{\displaystyle 2}\displaystyle c^{\displaystyle 2}})\).

Выражение в скобках почти не отличается от единицы, поэтому при малых \(t\) имеем:

\(\upsilon \approx \frac{Ft}{m}= at\).

Здесь \(a= F/m\) — ускорение тела. Мы получили результат, хорошо известный нам из классической механики: скорость тела линейно растёт со временем. Это и не удивительно — при малых временах движения скорость тела также невелика, поэтому мы можем пренебречь релятивистскими эффектами и пользоваться обычной механикой Ньютона.

Теперь переходим к большим временам. Преобразуем формулу ( 13) по-другому:

\(\upsilon \approx \frac{\displaystyle cFt}{\displaystyle Ft\sqrt{\displaystyle 1+\frac{\displaystyle m^{\displaystyle 2}\displaystyle c^{\displaystyle 2}}{\displaystyle F^{\displaystyle 2}\displaystyle t^{\displaystyle 2}}}}= \frac{\displaystyle c}{\sqrt{1+\frac{\displaystyle m^{\displaystyle 2}\displaystyle c^{\displaystyle 2}}{\displaystyle F^{\displaystyle 2}t^{\displaystyle 2}}}}\).

При больших значениях \(t\) имеем:

\(\frac{\displaystyle m^{\displaystyle 2}\displaystyle c^{\displaystyle 2}}{\displaystyle F^{\displaystyle 2}\displaystyle t^{\displaystyle 2}}\ll 1\),

и тогда:

\(\upsilon \approx \frac{c}{1+\frac{1}{2}\frac{m^{2}c^{2}}{F^{2}t^{2}}}\approx c(1-\frac{m^{2}c^{2}}{2F^{2}t^{2}})\).

Хорошо видно, что при \(t \to \infty\) скорость тела \(\upsilon \) неуклонно приближается к скорости света \(c\), но всегда остаётся меньше \(c\) — как того и требует теория относительности.

Зависимость скорости тела от времени, даваемая формулой ( 13), графически представлена на рис. 2.

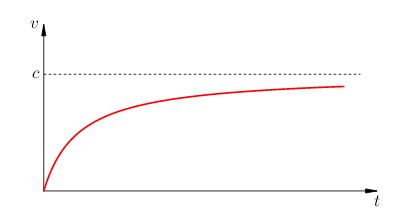Рис. 2. Разгон тела под действием постоянной силы

Начальный участок графика — почти линейный; здесь пока работает классическая механика. Впоследствии сказываются релятивистские поправки, график искривляется, и при больших временах наша кривая асимптотически приближается к прямой \(\upsilon =c\).