Тонкие линзы. Ход лучей.

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: линзы, оптическая сила линзы

Взгляните ещё раз на рисунки линз из предыдущего листка: эти линзы обладают заметной толщиной и существенной кривизной своих сферических границ. Мы намеренно рисовали такие линзы - чтобы основные закономерности хода световых лучей проявились как можно более чётко.

 

к оглавлению ▴

Понятие тонкой линзы.

 

Теперь, когда эти закономерности достаточно ясны, мы рассмотрим очень полезную идеализацию, которая называется тонкой линзой.
В качестве примера на рис. 1 приведена двояковыпуклая линза; точки \(O_{1}\) и \(O_{2}\) являются центрами её сферических поверхностей, \(R_{1}\) и \(R_{2}\)- радиусы кривизны этих поверхностей. \(O_{1}O_{2}\) - главная оптическая ось линзы.

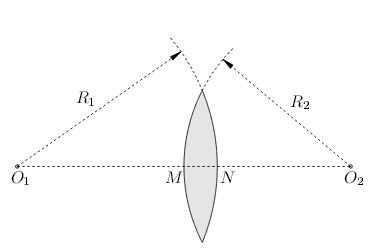Рис. 1. К определению тонкой линзы

 

Так вот, линза считается тонкой, если её толщина \(MN\) очень мала. Нужно, правда, уточнить: мала по сравнению с чем?

Во-первых, предполагается, что \(MN \ll R_{1}\) и \(MN \ll R_{2}\). Тогда поверхности линзы хоть и будут выпуклыми, но могут восприниматься как "почти плоские". Этот факт нам очень скоро пригодится.
Во-вторых, \(MN \ll a\), где \(a\) - характерное расстояние от линзы до интересующего нас предмета. Собственно, лишь в таком случае мы и
сможем корректно говорить о "расстоянии от предмета до линзы", не уточняя, до какой именно точки линзы берётся это самое расстояние.

Мы дали определение тонкой линзы, имея в виду двояковыпуклую линзу на рис. 1. Это определение без каких-либо изменений переносится на все остальные виды линз. Итак: линза является тонкой, если толщина линзы много меньше радиусов кривизны её сферических границ и расстояния от линзы до предмета.

Условное обозначение тонкой собирающей линзы показано на рис. 2.

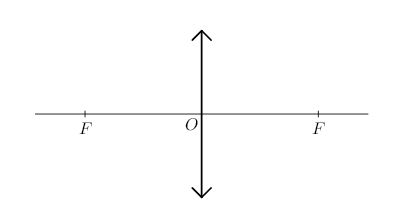Рис. 2. Обозначение тонкой собирающей линзы

 

Условное обозначение тонкой рассеивающей линзы показано на рис. 3.

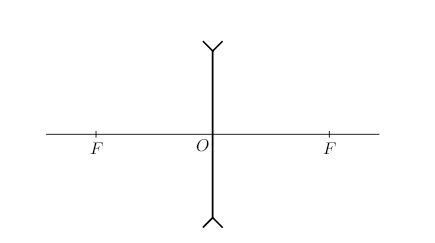Рис. 3. Обозначение тонкой рассеивающей линзы

 

В каждом случае прямая \(FF\) - это главная оптическая ось линзы, а сами точки \(F\) - её
фокусы. Оба фокуса тонкой линзы расположены симметрично относительно линзы.

 

к оглавлению ▴

Оптический центр и фокальная плоскость.

 

Точки \(M\) и \(N\), обозначенные на рис. 1, у тонкой линзы фактически сливаются в одну точку. Это точка \(O\) на рис. 2 и 3, называемая оптическим центром линзы. Оптический центр находится на Пересечении линзы с её главной оптической осью.

Расстояние \(OF\) от оптического центра до фокуса называется фокусным расстоянием линзы. Мы будем обозначать фокусное расстояние буквой \(f\). Величина \(D\), обратная фокусному расстоянию, есть оптическая сила - линзы:

\(D=\frac{\displaystyle 1}{\displaystyle f}\).

Оптическая сила измеряется в диоптриях (дптр). Так, если фокусное расстояние линзы равно 25 см, то её оптическая сила:

\(D=\frac{\displaystyle 1}{\displaystyle 0,25}=4\) дптр

Продолжаем вводить новые понятия. Всякая прямая, проходящая через оптический центр линзы и отличная от главной оптической оси, называется побочной оптической осью . На рис. 4 изображена побочная оптическая ось - прямая \(OP\).

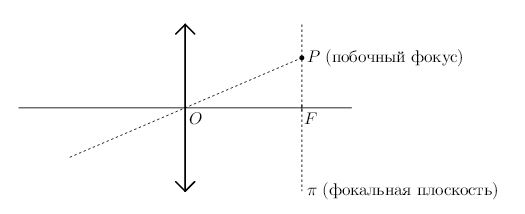Рис. 4. Побочная оптическая ось, фокальная плоскость и побочный фокус

 

Плоскость \(\pi \), проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость, таким образом, параллельна плоскости линзы. Имея два фокуса, линза соответственно имеет и две фокальных плоскости, расположенных симметрично относительно линзы.

Точка \(P\), в которой побочная оптическая ось пересекает фокальную плоскость, называется побочным фокусом. Собственно, каждая точка фокальной плоскости (кроме \(F\)) есть побочный фокус - мы ведь всегда сможем провести побочную оптическую ось, соединив данную точку с оптическим центром линзы. А сама точка \(F\) - фокус линзы - в связи с этим называется ещё главным фокусом.

То, что на рис. 4 изображена собирающая линза, никакой роли не играет. Понятия побочной оптической оси, фокальной плоскости и побочного фокуса совершенно аналогично определяются и для рассеивающей линзы - с заменой на рис. 4 собирающей линзы на рассеивающую.

Теперь мы переходим к рассмотрению хода лучей в тонких линзах. Мы будем предполагать, что лучи являются параксиальными, то есть образуют достаточно малые углы с главной оптической осью. Если параксиальные лучи исходят из одной точки, то после прохождения линзы преломлённые лучи или их продолжения также пересекаются в одной точке. Поэтому изображения предметов, даваемые линзой, в параксиальных лучах получаются весьма чёткими.

 

к оглавлению ▴

Ход луча через оптический центр.

 

Как мы знаем из предыдущего раздела, луч, идущий вдоль главной оптической оси, не преломляется. В случае тонкой линзы оказывается, что луч, идущий вдоль побочной оптической оси, также не преломляется!

Объяснить это можно следующим образом. Вблизи оптического центра \(O\) обе поверхности линзы неотличимы от параллельных плоскостей, и луч в данном случае идёт как будто через плоскопараллельную стеклянную пластинку (рис. 5).

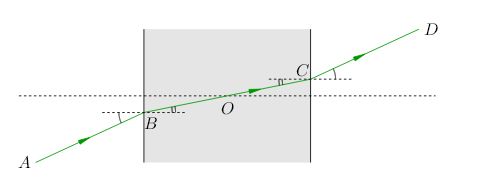Рис. 5. Ход луча через оптический центр линзы

 

Угол преломления луча \(AB\) равен углу падения преломлённого луча \(BC\) на вторую поверхность. Поэтому второй преломлённый луч \(CD\) выходит из плоскопараллельной пластинки параллельно падающему лучу \(AB\). Плоскопараллельная пластинка лишь смещает луч, не изменяя его направления, и это смещение тем меньше, чем меньше толщина пластинки.

Но для тонкой линзы мы можем считать, что эта толщина равна нулю. Тогда точки \(B, O, C\) фактически сольются в одну точку, и луч \(CD\) окажется просто продолжением луча \(AB\). Вот поэтому и получается, что луч, идущий вдоль побочной оптической оси, не преломляется тонкой линзой (рис. 6).

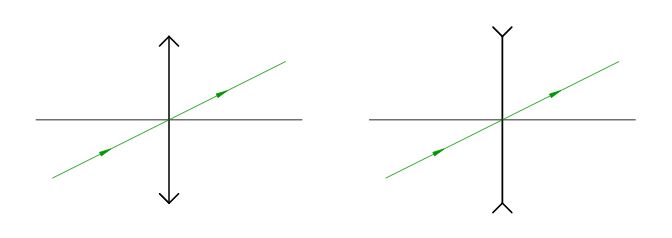Рис. 6. Луч, идущий через оптический центр тонкой линзы, не преломляется

 

Это единственное общее свойство собирающих и рассеивающих линз. В остальном ход лучей в них оказывается различным, и дальше нам придётся рассматривать собирающую и рассеивающую линзу по отдельности.

 

к оглавлению ▴

Ход лучей в собирающей линзе.

 

Как мы помним, собирающая линза называется так потому, что световой пучок, параллельный главной оптической оси, после прохождения линзы собирается в её главном фокусе (рис. 7).

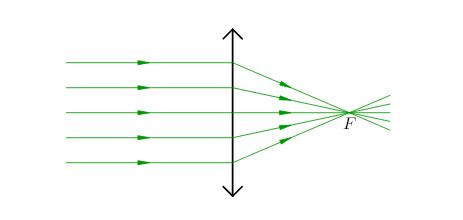Рис. 7. Параллельный пучок собирается в главном фокусе

 

Пользуясь обратимостью световых лучей, приходим к следующему выводу: если в главном фокусе собирающей линзы находится точечный источник света, то на выходе из линзы получится световой пучок, параллельный главной оптической оси (рис. 8).

Рис. 8. Преломление пучка, идущего из главного фокуса

 

Оказывается, что пучок параллельных лучей, падающих на собирающую линзу наклонно, тоже соберётся в фокусе - но в побочном. Этот побочный фокус \(P\) отвечает тому лучу, который проходит через оптический центр линзы и не преломляется (рис. 9).

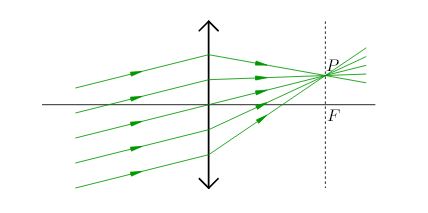Рис. 9. Параллельный пучок собирается в побочном фокусе

 

Теперь мы можем сформулировать правила хода лучей в собирающей линзе. Эти правила вытекают из рисунков 6-9,

1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления пойдёт через главный фокус (рис. 10).

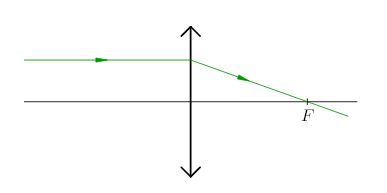Рис. 10. К правилу 2

 

3. Если луч падает на линзу наклонно, то для построения его дальнейшего хода мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Вот через этот побочный фокус и пойдёт преломлённый луч (рис. 11).

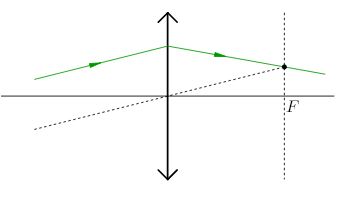Рис. 11. К правилу 3

 

В частности, если падающий луч проходит через фокус линзы, то после преломления он пойдёт параллельно главной оптической оси.

 

к оглавлению ▴

Ход лучей в рассеивающей линзе.

 

Переходим к рассеивающей линзе. Она преобразует пучок света, параллельный главной оптической оси, в расходящийся пучок, как бы выходящий из главного фокуса (рис. 12)

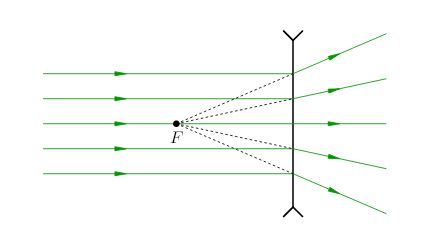Рис. 12. Рассеяние параллельного пучка

 

Наблюдая этот расходящийся пучок, мы увидим светящуюся точку, расположенную в фокусе \(F\) позади линзы.

Если параллельный пучок падает на линзу наклонно, то после преломления он также станет расходящимся. Продолжения лучей расходящегося пучка соберутся в побочном фокусе \(P\), отвечающем тому лучу, который проходит через через оптический центр линзы и не преломляется (рис. 13).

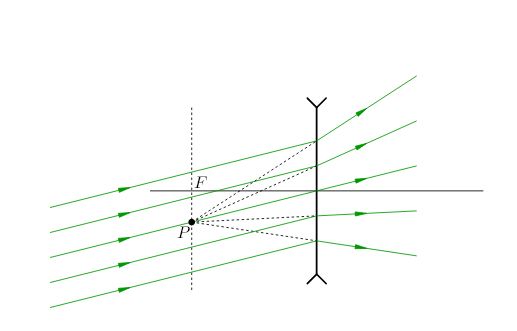Рис. 13. Рассеяние наклонного параллельного пучка

 

Этот расходящийся пучок создаст у нас иллюзию светящейся точки, расположенной в побочном фокусе \(P\) за линзой.

Теперь мы готовы сформулировать правила хода лучей в рассеивающей линзе. Эти правила следуют из рисунков 6, 12 и 13.

1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления начнёт удаляться от главной оптической оси; при этом продолжение преломлённого луча пройдёт через главный фокус (рис. 14).

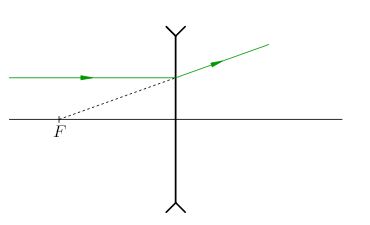Рис. 14. К правилу 2

 

3. Если луч падает на линзу наклонно, то мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Преломлённый луч пойдёт так, словно он исходит из этого побочного фокуса (рис. 15).

Рис. 15. К правилу 3

 

Пользуясь правилами хода лучей 1–3 для собирающей и рассеивающей линзы, мы теперь научимся самому главному - строить изображения предметов, даваемые линзами.

Разберем задачи ЕГЭ по теме: Тонкие линзы.

1. На экране с помощью тонкой линзы получено изображение предмета с пятикратным увеличением. Экран передвинули на 30 см вдоль главной оптической оси линзы. Затем при неизменном положении линзы передвинули предмет, чтобы изображение снова стало резким. В этом случае получилось изображение с трехкратным увеличением. На сколько пришлось передвинуть предмет относительно первоначального положения?
Дано:
Г₁=5
Г₂=3
а = 30 см = 0,3 м.
Найти:
Δd - ?

Решение.

При решении этой задачи главным является создание модели, которая поясняет изменения в увеличении линзы и позволяет правильно определить перемещение экрана и предмета. На представленных ниже рис.1 и рис.2 выполнены все необходимые построения для двух случаев задачи. Так как увеличение линзы уменьшается, то предмет смещается в сторону двойного фокуса. Именно в этом случае возможно уменьшение изображения, по сравнению с первым случаем.

Особое внимание надо обратить на фразу, что изображение снова стало резким. Это возможно только при выполнении всех соотношений в формуле тонкой линзы \(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}.\)

Для каждого случая запишем формулу тонкой линзы и учтем соотношения между d и f через значение увеличения (Г), даваемое линзой.

\(\frac{1}{d_1}+\frac{1}{f_1}=\frac{1}{F} ~~(1)\)

\(\frac{1}{d_2}+\frac{1}{f_2}=\frac{1}{F} ~~(2)\)

\(\frac{f_1}{d_1}= \)Г₁ \(=5 ~~(3)\), отсюда \(d_1=\frac{f_1}{5}.\)

\(\frac{f_2}{d_2}= \)Г₂ \(=3 ~~(4)\), отсюда \(d_2=\frac{f_2}{3}.\)

Тогда формулы (1) и (2) примут вид:

\(\frac{5}{f_1}+\frac{1}{f_1}=\frac{1}{F}\)

\(\frac{3}{f_2}+\frac{1}{f_2}=\frac{1}{F}\)

\(\frac{6}{f_1}=\frac{1}{F}~~(5)\)

\(\frac{4}{f_2}=\frac{1}{F}~~(6)\)

Остается решить следующую систему из двух уравнений:

\(
\begin{cases}
\frac{6}{f_1}=\frac{4}{f_2} \\
f_1-f_2=a
\end{cases}
\)

Решение этой системы можно провести с подстановкой численных значений.

\(\frac{6}{f_1}=\frac{4}{f_1=0,3}\)
\(6f_1-1,8=4f_1\)
\(2f_1=1,8\)
\(f_1=0,9\) (м). Тогда \(f_2=0,9-0,3=0,6\) (м)

\(d_1=\frac{0,9}{5}=0,18\) (м)

\(d_2=\frac{0,6}{3}=0,2\) (м)

\(\Delta d=0,2-0,18=0,02\) (м).

Ответ: 0,02 м

2. На оси ОХ в точке \(x_1=0\) находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием \(F_1=-20\) см, а в точке \(x_2=20\) см – тонкой собирающей линзы. Главные оптические ос обеих линз лежат на оси ОХ. На рассеивающую линзу вдоль оси ОХ падает параллельный пучок света из области х<0. Пройдя данную оптическую систему, лучи собираются в точке с координатой \(x_3=30\) см. Найдите фокусное расстояние собирающей линзы \(F_2\). Дано: \(x_1=0\) \(F_1=-20\) см = -0,2 м \(x_2=20\) см = 0,2 м \(x_3=30\) см = 0,6 м Найти: \(F_2\) - ? Решение На рисунке представлен ход лучей через систему рассеивающей и собирающей линз. При решении подобных задач необходимо рассматривать отдельно ход лучей сквозь каждую линзу.

Рассмотрим сначала ход лучей через рассеивающую линзу. Для этого воспользуемся формулой тонкой линзы и учтем, что \(d_1 \rightarrow \infty\), так как на рассеивающую линзу падает параллельный пучок света из области \(x<0\). Тогда дробь \(\frac{1}{d_1}\rightarrow 0\) и формула примет вид: \(-\frac{1}{f_1}=-\frac{1}{F_1}\) Перед \(f_1\) стоит знак (-), так как линза рассеивающая и она дает всегда мнимое изображение. Поэтому \(f_1=F_1=0,2\) (м). В точке S сформировалось мнимое изображение светового пучка, который падает на собирающую линзу из области \(x<0.\) Теперь отдельно рассмотрим собирающую линзу. Для нее расстояние \(d_2\) будет равно 0,4 м (согласно рисунку). Применим для собирающей линзы формулу тонкой линзы с учетом \(d_2\) и \(f_2\). Расстояние \(f_2=f=x_3-x_2\); \(f=0,6-0,2=0,4\) (м). \(\frac{1}{d_2}+\frac{1}{f_2}=\frac{1}{F}\) \(\frac{d_2+f_2}{d_2\cdot f_2}=\frac{1}{F}\) \(F=\frac{d_2\cdot f_2}{d_2+f_2}\) \(F=\frac{0,4 \cdot 0,4}{0,4+0,4}=0,2\) (м) = 20 (см). Ответ: 20 см. 3. Точечный источник света движется со скоростью v вокруг главной оптической оси собирающей линзы в плоскости, параллельной плоскости линзы на расстоянии d=15 см от линзы. Фокусное расстояние линзы F= 10 cм. Скорость движения изображения точечного источника света V=10 м/с. Найдите скорость движения источника света. Дано: d=15 см = 0,15 м F= 10 см = 0,1 м V=10 м/с Найти: v-? Решение. Для решения этой задачи воспользуемся формулой тонкой линзы. \(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\) \(\frac{1}{f}=\frac{1}{F}-\frac{1}{d}\) \(\frac{1}{f}=\frac{d-F}{Fd}\) \(f=\frac{Fd}{d-F}\) Проведем расчет для определения расстояния от линзы до изображения. \(f=\frac{0,1 \cdot 0,15}{0,15-0,1}=0,3\) (м). Полученный результат говорит о том, что увеличение линзы Г>1.

Г = \(\frac{0,3}{0,15}=2.\)

Точечный источник и его изображение будут двигаться с разными линейными скоростями, но в тоже самое время период их обращения, частота обращения и угловые скорости у них будут равными. Радиусы окружностей, которые будут описывать источник света и его изображения, будут отличаться в 2 раза. Радиус окружности изображения R будет превышать радиус окружности источника r в 2 раза \((\frac{R}{r}=2\) или \(\frac{r}{R}=\frac{1}{2}).\)

Воспользуемся формулой равенства периодов обращения.

\(T_1=\frac{2\pi r}{v}\)

\(T_2=\frac{2\pi R}{V}\)

\(T_1=T_2\)

\(\frac{2\pi r}{v}=\frac{2\pi R}{V}\)

\(v=\frac{r\cdot V}{R}\)

\(v=\frac{1\cdot 10}{2}=5\) (м/с)

4. Точечный источник света S расположен на расстоянии 40 cм от оптического центра тонкой собирающей линзы с фокусным расстоянием 0,2 м на её главной оптической оси АВ. На сколько сместиться вдоль прямой АВ изображение источника, если линзу повернуть на угол \(\alpha\)=30° относительно оси, перпендикулярной плоскости рисунка и проходящей через оптический центр линзы? Сделайте пояснительный чертеж, указав ход лучей в линзе для обоих случаев её расположения.

Дано:
\(d_1= 40\) cм = 0,4 м
F = 0,2 м
\(\alpha\) = 30°
Найти:
\(\Delta f\) - ?

Решение.

Применим формулу тонкой линзы для первого случая.

\(\frac{1}{d_1}+\frac{1}{f_1}=\frac{1}{F}\)

\(\frac{1}{f_1}=\frac{1}{F}-\frac{1}{d_1}\)

\(\frac{1}{f_1}=\frac{d_1-F}{Fd_1}\)

\(f_1=\frac{Fd_1}{d_1-F}\)

\(f_1=\frac{0,2\cdot 0,4}{0,4-0,2}=0,4\) (м).

Применим формулу тонкой линзы для второго случая.

\(\frac{1}{d_2}+\frac{1}{f_2}=\frac{1}{F}\)

\(\frac{1}{f_2}=\frac{1}{F}-\frac{1}{d_2}\)

\(\frac{1}{f_2}=\frac{d_2-F}{Fd_2}\)

\(f_2=\frac{Fd_2}{d_2-F}\)

Здесь необходимо учесть, что \(d_2=d_1\cos\alpha=0,4\cos30\textdegree \approx 0,35\) (м).

\(f_2=\frac{0,2 \cdot 0,35}{0,35-0,2}\approx 0,47\) (м).

Изображение источника во втором случае также формируется на прямой АВ. Для нахождения расстояния \(OS_2\) необходимо

\(OS_2\cos\alpha = f_2\)

\(OS_2=\frac{f_2}{\cos\alpha}\)

\(OS_2=\frac{0,47}{\cos 30\textdegree } = 0,54\) (м).

Таким образом, изображения источников в обоих случаях получились на прямой АВ на расстоянии \(\Delta f = 0,54-0,4=0,14\) (м).
Ответ: 0,14 м.

Если вам нравятся наши материалы - записывайтесь на курсы подготовки к ЕГЭ по физике онлайн