Центр подготовки к ЕГЭ > Курсы подготовки к ЕГЭ по физике > Закон Ома

Закон Ома

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон Ома для участка цепи, электрическое сопротивление.

Рассмотрим некоторый элемент электрической цепи постоянного тока. Это может быть что угодно: металлический проводник, раствор электролита, лампочка накаливания, газоразрядная трубка. . .
Будем менять напряжение $U$ , поданное на наш элемент, и измерять силу тока $I$ , протекающего через него. Получим функциональную зависимость $I = I(U)$ . Эта зависимость называется вольт-амперной характеристикой элемента и является наиважнейшим показателем его электрических свойств.

Вольт-амперные характеристики различных элементов цепи могут выглядеть по-разному.
Очень простой вид имеет вольт-амперная характеристика металлического проводника. Эту зависимость экспериментально установил Георг Ом.

Закон Ома для участка цепи

Оказалось, что сила тока в металлическом проводнике прямо пропорциональна напряжению на его концах: $I \sim U$ . Коэффициент пропорциональности принято записывать в виде $1/R$ :

$I=\frac{\displaystyle U}{\displaystyle R \vphantom{1^a}}.$ (1)

Величина $R$ называется сопротивлением проводника. Измеряется сопротивление в омах (Ом). Как видим, Ом=В/А.

Дадим словесную формулировку закона Ома.

Закон Ома для участка цепи. Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.

Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов.

Сформулированный закон имеет место для так называемого однородного участка цепи — участка, не содержащего источников тока. Закон Ома для неоднородного участка (на котором имеется источник тока) мы обсудим позже.

Вольт-амперная характеристика (1) является линейной функцией. Её графиком служит прямая линия (рис. 1).

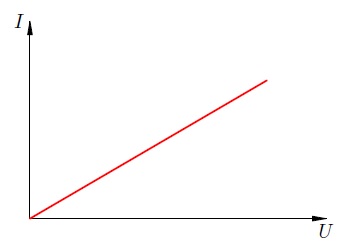
Рис. 1. Вольт-амперная характеристика металлического проводника

По этой причине металлические проводники (и электролиты) называются линейными элементами. А вот газоразрядная трубка, например, является нелинейным элементом — её вольт-амперная характеристика уже не будет линейной функцией. Но об этом мы поговорим позднее.

Электрическое сопротивление

А сейчас давайте подумаем вот о чём. Пусть к концам проводника приложено постоянное напряжение $U$ . Тогда на свободные заряды проводника действует сила со стороны стационарного электрического поля. Раз есть сила — значит, эти заряды должны двигаться с ускорением; скорость их направленного движения будет увеличиваться, а вместе с ней будет возрастать и сила тока. Но закон Ома гласит, что сила тока будет постоянной. Как же так?

Дело в том, что сила со стороны стационарного поля — не единственная сила, действующая на свободные заряды проводника.

Например, свободные электроны металла, совершая направленное движение, сталкиваются с ионами кристаллической решётки. Возникает своего рода сила сопротивления, действующая со стороны проводника на свободные заряды. Эта сила уравновешивает электрическую силу, с которой на свободные заряды действует стационарное поле. В результате скорость направленного движения заряженных частиц не меняется по модулю (точнее говоря, свободные электроны всё же двигаются равноускоренно, но только в промежутках между соударениями с ионами кристаллической решётки. В среднем же оказывается, что электроны перемещаются с постоянной скоростью); вместе с ней остаётся постоянной и сила тока.

Так что величина $R$ названа сопротивлением не случайно. Она и в самом деле показывает, в какой степени проводник «сопротивляется» прохождению тока.

Удельное сопротивление

Возьмём два проводника из одинакового материала с равными поперечными сечениями; пусть отличаются только их длины. Ясно, что сопротивление будет больше у того проводника, у которого больше длина. В самом деле, при большей длине проводника свободным зарядам труднее пройти сквозь него: каждый свободный электрон встретит на своём пути больше ионов кристаллической решётки. Аналогия такая: чем длиннее заполненная машинами улица, тем труднее будет через неё проехать.

Пусть теперь проводники отличаются только площадью поперечного сечения. Ясно, что чем больше площадь, тем меньше сопротивление проводника. Снова аналогия: чем шире шоссе, тем больше его пропускная способность, т. е. тем меньше его «сопротивление» движению машин.

Опыт подтверждает эти соображения и показывает, что сопротивление проводника прямо пропорционально его длине $l$ и обратно пропорционально площади поперечного сечения $S$ :

$R=\rho \frac{\displaystyle l}{\displaystyle S \vphantom{1^a}}.$ (2)

Коэффициент пропорциональности $\rho$ уже не зависит от геометрии проводника; он является характеристикой вещества проводника и называется удельным сопротивлением данного вещества. Величины удельных сопротивлений различных веществ можно найти в соответствующей таблице.

В каких единицах измеряется удельное сопротивление? Давайте выразим его из формулы (2):

$\rho= \frac{\displaystyle RS}{\displaystyle l \vphantom{1^a}}.$

Получим:

$[\rho]= \frac{\displaystyle OM \cdot M^2}{\displaystyle M \vphantom{1^a}}=OM \cdot M$

Однако такая «теоретическая» единица измерения не всегда удобна. Она вынуждает при расчётах переводить площадь поперечного сечения в квадратные метры, тогда как на практике чаще всего речь идёт о квадратных миллиметрах (для проводов, например). На такой случай предусмотрена «практическая» единица:

$\frac{\displaystyle OM \cdot MM^2}{\displaystyle M \vphantom{1^a}}$

В таблице задачника Рымкевича удельное сопротивление даётся как в «теоретических» единицах, так и в «практических».

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Закон Ома» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 09.05.2023